초간단 선형대수를 뜬금없이 살펴보았습니다만, 어찌 보면 나중에 필요하니까 살펴본 것이기도 하고, 여기에 덧붙여서 Eigen Value와 Eigen Vector를 꼭 짚었는데, 이런 것들을 다루고 넘어가야지만 우리가 이해할 수 있는 분석 방법이 하나 있어서 그랬던 것인데요, 그게 PCA라는 겁니다. 풀네임은 Pincipal Component Analysis이고 한국어 버전은 주성분 분석입니다. 어쨌든 곧바로 살펴보기 위해서는 Eigen Value와 Eigen Vector가 뭔지는 알아야 이야기할 수 있는 것이어서 살펴보았으니 뜬금없었다고 생각 마시고 이해해 주세요.
어쨌든 PCA(pincipal Component Analysis)는 한국어로 번역하면 주성분분석이라는 말로 해석되어 있는데 처음에 이 용어를 접하면 주성분이 무엇인지 찾아내는 것이겠지라는 안이한 생각을 갖게 됩니다. 주성분을 왜 찾아내고, 찾아내서 뭐에 쓴다는 말인가를 곰곰이 생각해 볼 필요가 있겠죠. 게다가, 뜬금없이 차원 축소니, 압축이니 하는 말이 따라 나옵니다. 음. 그렇다면 말 그대로 주성분을 분석해서 차원 축소니, 압축이니 하는 것들을 하겠습니다만, 그 역시 감이 오지 않는 용어입니다. 역시 압축이라는 용어가 나오니까, 대표적인 값으로 압축을 한다면 평균이 가장 좋은 예가 될 수 있겠습니다. 뭐, 그런 의미입니다.
실제적인 예를 들면, 어떤 학교의 학생들의 성적을 내는데, 그 과목이 국어, 영어, 수학, 체육이라고 해 봅시다. 그래서 학생별로 이 과목들의 점수를 보고 있는데, 각 과목의 점수 상관도를 보았더니, 어? 국어와 영어는 서로 상관도가 좀 있네? 그러면 이 두과목을 1개로 합쳐서 언어라는 것으로 합칠 수 있을까? 그러면 2개 과목을 1개로 줄여서 조금 더 복잡도를 낮출 수 있을 텐데.. 말입니다. 그쵸? - 2개 과목을 1개의 score로 압축한다! 는 의미도 되겠군요. - 꽤나 흥미진진한 이야기로군요.
일단 PCA를 통해 무엇을 하고 싶은지를 정리해 보면 조금은 이해에 도움이 되겠습니다. PCA는 고차원의 데이터를 - 데이터의 Column이 많은 Column을 합쳐서 저차원의 데이터로 만드는 것입니다. 조금 어렵긴 하지만 가장 쉬운 2차원 데이터를 이용해서 들여다보면 훨씬 이해가 쉽습니다.
예를 들어, 다음과 같은 2차원 데이터가 있다고 합시다. 이 2차원 데이터를 1개의 차원의 데이터로 합칠 수 있을까요?

다시 말해 이 데이터를 1차원, 즉 1개의 축으로 한꺼번에 표현할 수 있을까요? 제일 먼저 문득 생각이 드는 것은 ➊ x₁축으로 Projection을 하거나, ➋ x₂축으로 Projection하는 것을 생각해 볼 수 있겠습니다. 그런데 말입니다. 그게 말처럼 쉽지 않습니다.

➌ x₁축으로 Projection을 했을 경우에 적절하게 모든 정보를 잃지 않도록 - 데이터들이 겹치지 않도록 - Projection이 어렵습니다. ➍ x₂축도 당연한 이야기입니다. 이렇게 해서는 정보를 잃지 않고 1개의 축(1차원)으로 모든 정보를 표현하기가 어렵습니다. 두 Projection 모두 겹치는 것들이 나올 수 있으니까요. 이래도 저래도 문제가 있군요.
2차원의 데이터를 겹차지 않고 1개의 차원으로 합칠 수만 있다면 데이터를 압축했다고 볼 수 있겠는데 말이죠. 그렇기만 하다면, 차원을 축소했다고도 할 수 있겠습니다. 어쨌든 이런 선을 어떻게든 찾아내면 좋겠는데... 그러면 이런 건 어떨까요?
그러면 이런 식의 가운데를 가로지르는 축이 있다면 좀 나을까요?

오, 그런대로 느낌이 좋은 접근이라고 생각합니다.
그러니까, 가로지르는 선에 Projection하면 겹치는 것이 별로 없고, 효율적으로 하나의 선 위에 데이터를 표시할 수 있지 않겠는가... 오. 획기적입니다. 그런데 말이죠. 말이 쉽지, 뭐, 이 선을 어떻게 찾아내느냐 그것이 문제가 되겠군요. 흠.


결론적으로는 이런 식으로 2개차원의 데이터를 1개 차원으로 몰아넣어서 "합"칠 수 있게 될 수 있지 않을까 하는 매우 그럴듯한 이야기 입죠. 데이터들을 정사영 시켜서 차원을 낮추는 것인데, 어떤 벡터에 데이터들을 정사영 시켜야 원래의 데이터의 구조를 제일 잘 유지할 수 있을까? 에 대한 해답을 찾아가는 겁니다.
이런 알흠다운 선의 조건을 말하자면, 데이터들의 분산이 넓은 쪽으로 찾아야 하겠고, 그러니까 그 선에 데이터들이 가장 넓은 방향으로 펼쳐져 있어서 Projection 해서 합친 후의 데이터를 잘 살릴 수 있도록 해야겠습니다. PCA, 자원 축소는 핵심 정보는 유지하면서 쓸데없는 정보를 제거하기 위해서 하는 것이니까요.
자, 그러면 이런 알흠다운 선을 찾아내는 방법을 이야기해야 하겠는데, 그 방법이라는 것이 엉뚱한 곳에서 접근하게 되어서 조금 벙찌게 되는데, 전혀 관계없어 보이는 선형대수에서의 Eigen Vector와 Eigen Value를 통해서 그 알흠다운 선을 찾아냅니다. 오. 그러면 Eigen Vector를 다룬다는 것은 분명히 데이터의 모양새를 설명하는 행렬이 있다는 뜻인데, 그것이 바로 공분산 행렬입니다. 오홋.

지금부터 새로운 시각으로 이 Eigen Vector라는 것을 보자면,
그렇다면, 어떤 2개의 데이터 짝의 분포가 있는데 그 데이터의 분포를 설명하기 위한 행렬이 무엇일까 하면 공분산 행렬입니다. 이게 무슨 이야기인가? 하면, 공분산 행렬이 어떻게 생겼는지 잘 알고 있잖아요?
$$
\begin{bmatrix}
S_{X}^2 & S_{XY} \\
S_{XY} & S_{Y}^2 \\
\end{bmatrix}
$$
이거인데요, 이 행렬의 의미는 각각의 축으로 퍼진 정도를 나타냅니다요. 공분산의 정의는 다음과 같습니다.
$$
S_{XY} = \operatorname{Cov}(X, Y)=\sigma_{x y}=E\left[\left(\mathrm{X}-\mu_z\right)\left(\mathrm{Y}-\mu_y\right)\right]=E(\mathrm{XY})-\mu_x \mu_y
$$
이 공분산행렬의 각 Element의 의미를 따져보면, 다음과 같습니다.

그렇다면, 일단 공분산이 0인 경우에는 서로 uncorrelated 한데요, 그런 경우에는 각각의 분산에 비례하여 데이터들이 흩어져 있습니다.

이때 서로의 공분산이 있으면 상관관계가 생기기 시작하는데, 상관관계가 생기기 시작하면 양이든 음이든 방향성을 갖게 되어 있다는 점. 그리고 일반적인 행렬과 다르게, 공분산 행렬은 무조건 양수만 가지기 때문에 이런 설명이 좀 더 쉽게 될 수 있습니다.

게다가 공분산 행렬의 기저에 의한 선형 조합으로 모든 데이터를 표현할 수 있다고 생각하면 뙇! 매직아이가 눈앞으로 튀어나오게 됩니다. 보통 이해하기 어려운 부분이 바로 이 부분인데 그냥 원시 데이터 (X, Y) 쌍 데이터를 찍은 것에 대해서 공분산 행렬을 계산하긴 했는데, 공분산 행렬로 어떻게 기하학적으로 데이터를 거꾸로 설명하지?라는 부분이 연결이 안 되니까 공분산 행렬이 뜬 구름처럼 느껴졌을 것이라 생각합니다.

예를 들어, 실제로는 공분산 행렬이 설명하는 데이터는 x 데이터의 분산에 비해 어디에 위치하는지, y 데이터의 분산에 비해 어디에 위치하는지, 그리고 공분산에 비해 어디에 위치하는지를 설명합니다. 이제는 데이터는 공분산 행렬로 설명이 된다는 무시무시한 결과를 가슴에 품고요, 추가해서 Eigen Vector, Basis가 어떤 것인지를 보자면,

으헛. 바로 이 순간이 제일 중요한 시점인데, Eigen Vector의 의미는 행렬이 벡터에 영향을 미치는 주축 방향이니까, 공분산 행렬의 Eigen Vector는 데이터가 어떤 방향으로 가장 크게 분산되어 있는지를 알려줍니다. 그러니까 어떤 행렬에 대해서 그 행렬의 Dominant Eigen Vector 방향으로 데이터가 가장 길게 늘어서고요, Eigen Value만큼의 크기를 갖습니다. 그렇다면!!! 이 Eigen Vector라는 것에 데이터들을 정사영Projection 한다면 겹치는 것이 가장 적게 (잃어버리는 정보가 가장 적게) 할 수 있겠습니다. 처음 시작할 때 우리가 찾던 알흠다운 선이 될 수 있는 충분한 조건을 갖게 되겠습니다. 다시 말해, 이 공분산의 Eigen Vector가 바로 분산이 제일 큰 방향을 가리키게 되는데, 이걸 Principal Component라고 합니다. 분산이 제일 크니까 그 선으로 Projection했을 때 그나마 정보손실이 가장 적게 데이터들이 안착하겠습니다. 그냥 생각해 봐도 Eigen Value가 크면 분산이 크겠죠? 그러니까 Dominant Eigen Vector가 알흠다운 선, Principal Component가 되겠습니다

오, 이렇게 해서 알흠다운 선을 찾아서 Projection한다! 그렇게 해서 2개의 차원을 1개의 차원으로 줄일 수 있다! 뭐 그런 멋진 이야기인 것입니다. 예를 들면 이 좌표계에서 (2, 3)라는 데이터는 $2\cdot(S_X^2 + S_{XY}) + 3\cdot(S_Y^2 + S_{YX})$ 이니까, 평균으로부터 X의 분산의 2배, 평균으로부터 Y의 분산의 3배, 평균으로부터 XY공분산의 5배 떨어진 곳의 점이라고 생각하면 좋겠습니다.
사실 이제까지는 2개 차원을 1개 차원으로 줄인다는 이야기를 주구장창하긴 했습니다만, n개 차원은 n개의 Principal Component가 있다고 했잖아요? 그러니까 많은 차원을 가장 효율적인 개수의 차원으로 줄일 수도 있습니다. 오, 그렇군요. 이것이 가능한 이유가 공분산 행렬은 대칭 행렬이잖아요? 그러면 어떤 일이 벌어지냐면 n차원의 공분산 행렬의 고유 벡터들이 서로 Orthogonal(직교)합니다(와). 그러니까 압축을 할 때, Eigen Value가 큰 순으로 Projection을 하면 서로 겹치지 않는 방향으로 분산이 큰 순으로 데이터를 압축할 수 있습니다.
지금까지의 이야기를 조금 유식한 말로 바꾸어서 단순하게 정리하면 다음과 같은 이야기가 되겠습니다.
㉠ PCA란 차원 축소를 이용해서 복잡한 데이터들을 단순하게 만드는 것인데요, 고차원의 데이터를 저차원으로 단순하게 만드는 것을 말함
㉡ 그런데, 단순하게 고차원을 저차원으로 옮기면 겹치면 정보의 유실이 일어남.
㉢ 그러니까 정보의 유실이 최대한 일어나지 않도록 데이터의 분산이 가장 넓은 축을 찾는 것이 아이디어임.
㉣ 이때 Principal Component는 Covariance Matrix의 Eigen Vector임
㉤ 여러 차원에서 Eigen Value가 큰 녀석이 가장 큰 variance를 가지는 축이 된다는 거짓말 같은 이야기…
㉥ n개 차원을 k개 차원으로 압축하고 싶을 때는 Eigen Value가 가장 큰 Eigen Vector를 e0라고 한다면, 이 e0와 직교하며, e0 다음으로 분산(Eigen Value)이 큰 e1 고유 벡터에 또 Projection, 그리고 또 같은 짓을 ek까지 계속하면 된다는 사실. - 이것은 공분산 행렬이 Symmetry하기 때문에 가능합니다. -
이렇게 하면 압축한다는 의미가 잘 드러나고, PCA로 압축을 하면 비슷한 컬럼들의 종합점수를 잘 계산하는 것이라고 생각할 수도 있겠습니다.
그러면 실제로 PCA를 통해서 압축하는 일을 해 봅시다. 다음과 같은 아기들에 대한 데이터가 있다고 합시다.
몸무게 나이(개월)치아강도 손톱길이 출생지
0 33 48 19 1 서울
1 36 64 12 3 부산
2 34 53 18 2 경기도
3 40 70 5 2 제주도
4 32 44 20 3 서울
5 37 66 10 1 강원도
6 35 59 15 2 평양
7 34 60 17 3 경상도
8 37 60 15 3 전라도
9 33 44 23 2 충청도
아기들에 대한 몸무게, 나이(개월), 치아 강도, 손톱 길이, 출생지 데이터인데 출생지를 빼고 나머지 데이터를 생각한다면 4차원 데이터입니다. 이 데이터를 다룰 때 4차원 데이터를 모두 고려하여 다룰 것이냐, 아니면 차원수를 줄여서 다룰 수 있을 것이냐를 생각해 볼 수 있겠습니다. - 4차원이라고 함은 4개의 컬럼을 이야기하는 것이고 Feature라고 부릅니다. - 지금은 4차원밖에 안 되지만 이게 100차원, 200차원이 되게 되면, 많이 복잡한 이야기가 됩니다. 그래서 데이터를 다룰 때 Feature Selection, Feature Extraction이라는 걸 해서 단순화가 필요하게 됩니다.
Feature Selection : 불필요한 Feature를 버림
Feature Extraction : 원본 데이터의 Feature들의 조합으로 새로운 Feature를 생성하는 것. 보통 적은 차원으로 Mapping하는 것을 의미
이중에 PCA는 새로운 Feature를 생성하는 Extraction의 개념인데, 차원 축소를 해서 Feature Extraction을 하게 됩니다. 어떻게 Extraction하면 좋을지는 보통 상관 분석에서부터 시작하는 것이 편리한 방법인데, 당연하게도 비슷한 녀석을 묶어서 관리하면 좋으니까 그렇습니다.
df_baby.corr()
>
몸무게 나이(개월) 치아강도 손톱길이
몸무게 1.000000 0.901324 -0.933167 -0.069720
나이(개월) 0.901324 1.000000 -0.933849 0.006149
치아강도 -0.933167 -0.933849 1.000000 0.112160
손톱길이 -0.069720 0.006149 0.112160 1.000000
이걸 봤더니 어라, 0.9가 넘는 쌍이 3개나 있습니다. (나이-몸무게), (치아강도-몸무게), (나이-치아강도) 오 그렇군요. 그렇다면, 이 쌍들이 어떤지 한번 볼까요? 이때! 손톱길이는 그다지 별로 연관성이 없어 보이니까 고려를 배제하는 것이 좋겠습니다.
먼저, X와 Y의 형태로 데이터를 분리해 내고요.
X = df_baby[['몸무게', '나이(개월)', '치아강도']].copy()
Y = df_baby['출생지']
몸무게-나이(개월)를 들여다보면,
X.plot(x='몸무게', y='나이(개월)',kind='scatter')
음~ 관련 있어 보이고, 겹치는 데이터도 보이네요.
또, 몸무게-치아강도도 보면,
X.plot(x='몸무게', y='치아강도',kind='scatter')
이렇고요, 당연히 관련 있어 보이고, 겹치는 데이터도 보이네요. 좋습니다.
마지막으로 치아강도와 나이(개월)의 관계를 들여다보면,
X.plot(x='치아강도', y='나이(개월)',kind='scatter')

헤헿, 관련 있어 보이고, 겹치는 데이터도 보입니다.
이렇다면, 요 3가지(3차원)의 데이터를 1차원으로 만들어서 관리한다면 좋겠군요.
그러니까, 요 3가지 데이터를 표준 정규화를 한 후에 Covariance Matrix를 구한 후에 Eigen Vector에 Projection한 후에 1차원으로도 잘 표현하고 있는지 보면 좋겠군요.
from sklearn.preprocessing import StandardScaler
Xstdnorm = StandardScaler().fit_transform(X)
>
array([[-0.91304348, -1.01236401, 0.71942469],
[ 0.39130435, 0.82829783, -0.67945665],
[-0.47826087, -0.43715719, 0.5195845 ],
[ 2.13043478, 1.51854602, -2.07833799],
[-1.34782609, -1.47252947, 0.91926488],
[ 0.82608696, 1.05838056, -1.07913704],
[-0.04347826, 0.253091 , -0.07993608],
[-0.47826087, 0.36813237, 0.31974431],
[ 0.82608696, 0.36813237, -0.07993608],
[-0.91304348, -1.47252947, 1.51878546]])
데이터를 표준정규화를 할 때는 sklearn의 StandardScaler를 이용하면 편리하게 할 수 있습니다. 참고로 fit_transform은 fit은 입력 데이터의 표준편차 등을 찾아내는 것, transform은 데이터를 구한 표준편차를 이용해서 정규화하는 것입니다.
그러면, numpy를 이용해서 Covarinace Matrix를 구하고요,
columns = Xstdnorm.T
covariance_matrix = np.cov(columns)
> # columns
[[-0.91304348 0.39130435 -0.47826087 2.13043478 -1.34782609 0.82608696
-0.04347826 -0.47826087 0.82608696 -0.91304348]
[-1.01236401 0.82829783 -0.43715719 1.51854602 -1.47252947 1.05838056
0.253091 0.36813237 0.36813237 -1.47252947]
[ 0.71942469 -0.67945665 0.5195845 -2.07833799 0.91926488 -1.07913704
-0.07993608 0.31974431 -0.07993608 1.51878546]]
> # covariance matrix
[[ 1.11111111 1.0014712 -1.03685201]
[ 1.0014712 1.11111111 -1.0376103 ]
[-1.03685201 -1.0376103 1.11111111]]
Eigen Vector와 Value를 구합니다!
eig_vals, eig_vecs = np.linalg.eig(covariance_matrix)
>
Eigen Vectors
[[-0.57504939 -0.71089114 0.40490985]
[-0.57519393 0.7032635 0.41781862]
[ 0.58178187 -0.00736465 0.81331151]]
>
Eigen Values
[3.16182516 0.10964386 0.06186432]
3차원의 데이터에 대한 Eigen Value와 Vector는 당연히 3개가 나옵니다. 우리는 이 중에서 가장 Eigen Value가 큰 Vector를 사용할 것이기 때문에 이것은 eig_vecs.T[0]입니다. - np.linalg.eig는 Descending으로 정렬된 결과가 나옵니다. -
그러면 가장 큰 Eigen Vector에 데이터를 Projection해 보겠습니다. Projection하는 방법은 대상 벡터에 Inner Product - dot -을 하면 됩니다.
X_projected = Xstdnorm.dot(eig_vecs.T[0])
>
array([ 1.52589897, -1.09674677, 0.82875862, -3.30770303, 2.15686822,
-1.71163723, -0.16707962, 0.24929756, -0.73329366, 2.25563695]
이것이 가장 최종 결과입니다. 아하하
최종 결과물을 만들어내기 위해서
df_result = pd.DataFrame(X_projected, columns=['PC1'])
df_result['label'] = Y
print(df_result.head(4))
이렇게 데이터 몇 개만 보면,
PC1 label
0 1.525899 서울
1 -1.096747 부산
2 0.828759 경기도
3 -3.307703 제주도
이렇게 볼 수가 있고요. 이걸 그려보면 좋겠네요. 한 축에 그려보기 위해서
df_result['y-'] = 0
로 놓고,
df_result.plot(x="PC1", y="y-", kind="scatter")
이렇게 그려보면,
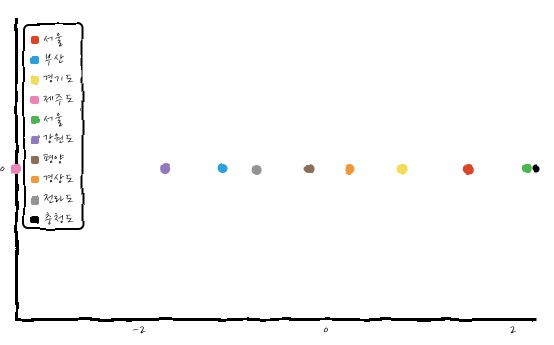
요렇게 이쁘게 압축된 것을 볼 수 있겠습니다. 그러면 얼마나 이쁘게 압축되는지에 대한 지표가 있는데, 전체 Eigen Value들 중에 Projection한 Eigen Value가 얼마나 차지하는지로 표시를 하거든요?
eig_vals[0] / sum(eig_vals)
>
0.9485475467310901
이렇게 구하고서는 Dominant Eigen Vector가 전체의 95%를 설명하고 있다고 읽습니다.
마지막으로 이렇게 압축한 데이터 나이(개월)-몸무게-치아강도 3가지를 압축했으니까, 이름을 다시 짓는다면 발달사항 정도로 압축해서 관리할 수 있겠습니다.
그렇다면, PCA를 이용하여 압축한 데이터는
df_baby['발달사항'] = df_result['PC1'].copy()
df_baby.drop(['몸무게', '나이(개월)', '치아강도'], axis=1, inplace=True)
이런 식으로 정리해 주면,
손톱길이 출생지 발달상황
0 1 서울 1.525899
1 3 부산 -1.096747
2 2 경기도 0.828759
3 2 제주도 -3.307703
4 3 서울 2.156868
5 1 강원도 -1.711637
6 2 평양 -0.167080
7 3 경상도 0.249298
8 3 전라도 -0.733294
9 2 충청도 2.255637
이런 식으로 정리할 수 있겠습니다. 데이터가 발달상황 하나로 확 압축되어 줄었죠! 굉장히 긴 이야기를 하였습니다만, PCA가 무엇인지 확실하게 알게 되었다면 그것으로 만족입니다.

Covariance Matrix에서 Eigen Vector가 가장 Projection하기 좋은 Variance가 가장 넓은 반경을 커버하는 선이라는 결과를 잘 기억할 수 있도록 설명했는데, 실제로 수학적으로는 Principal Component의 Varaince가 가장 큰 Line을 라그랑주 승수 법으로 찾으면 그것이 Eigen Vector일쎄? 라는 건데, 간단하게 보면
PC의 제곱은 데이터의 분산이므로 Transpose해서 곱하면 되니까, PC의 분산 Var(PC)는
$
\begin{aligned}
Var(PC) &= \cfrac{1}{n-1}PC \cdot PC^T \\
&= \cfrac{1}{n-1} AXX^TA^T \because PC=AX \\
&= ARA^T \because R = \cfrac{1}{n-1}X X^T\,\, covariance \,matrix
\end{aligned}
$
이때, $L = ARA^T - \lambda(AA^T-I) $를 풀면 라그랑주 승수법을 이용하는 것이 됩니다. 제약조건이 왜 $AA^T-I$인가를 이야기 한다면, A는 어떤 벡터인지는 모르겠지만, X를 표현하기 위한 단위 벡터이므로 그 크기가 1이어야 한다는 의미입니다. 결국,
$$\cfrac{\partial L}{\partial A} = 2RA - 2\lambda A = 0$$
$$\therefore RA = \lambda A$$
이것은 $ AX = \lambda X$의 꼴에서 X는 A에 대한 고유 벡터라는 점을 상기해 보면, 최종식에서의 A는 R에 대한 고유 벡터이고, 그러니까 R에 대한 고유 벡터를 구하면 그게 A이고 이게 Var(PC)를 최대로 하는 벡터이다라는 뜻입니다. 별거 아니긴 한데, 이렇게 보면 수학적으로 유도되는 것은 알겠지만 말이죠. 도저히 정을 붙이기 힘드니까, 참고로 알고 있으면 좋겠습니다.

PCA의 진정한 파워는 공분산 행렬의 Eigen Vector들이 서로 수직 한다는 데 있습니다. 이게 Eigen Vector들이 서로 수직 하기 때문에 각 Eigen Vector들끼리 완전히 관계를 끊어버릴 수 있다는 점이죠. 이렇게 하면 좋은 게 다중공선성이라는 것을 없앨 수가 있는데, 다중공선성은 이전에 이야기했듯이 독립변수끼리 같이 비슷하게 같이 움직이는 독립변수 중에 대표적인 1개 독립변수 하나만 있으면 대충 어떤 식으로 회귀 모델에 그 변수가 기여하는지 알 수 있겠는데, 이것들이 모두 모델에 포함되면 독립변수 하나만 있을 때 보다 그 두 개 변수의 합 때문에 그 변수의 합의 분산이 1개 있을 때 보다 커져버려서 회귀 모델의 계수의 분산을 크게 할 수 있다는 것이라고 했으니까, 당연히 이런 걸 없앨 수 있겠죠. - 이걸 없앤다고 더 좋다고만은 할 수 없습니다만. 그런 이야기는 마음의 편안함을 위해서 나중에 하는 것이 좋겠습니다. -
 친절한 데이터 사이언스 강좌 글 전체 목차 (정주행 링크) -
친절한 데이터 사이언스 강좌 글 전체 목차 (정주행 링크) - 

댓글