이미 Gradient Descent에 대한 컨셉에 대해서 많은 사람들이 익숙해 있을지도 모르겠다는 생각이 들었지만, 이걸 짚고 넘어가지 않으면 뭔가 앙꼬 없는 호빵 같은 이야기의 전개가 될 것 같아서 하려고 합니다. - 어차피 나중에 신경망 모형을 다룰 때에는 알아야 하니까요. - Gradient Descent는 경사 하강법이라고도 많이 부르는데, 처음에 이 용어를 들었을 때에는 경사가 하강한다니 이건 무슨 의미인가 싶었는데, 경사를 따라 하강한다는 의미라는 걸 알면 조금은 시작하기 편할 거라 생각합니다.
경사를 하강한다는 의미는 이제까지 다뤄왔던 Cost를 함수로 보고, 이 Cost함수가 Convex 형태일 때 최소값을 찾아가는 방법인데, Cost 함수의 경사를 따라 내려가면서 최소값을 찾아간다는 의미입니다.
여기까지가 일반적인 경사하강법의 설명인데, Gradient를 라그랑주 승수법에서 이미 살펴 봤잖아요? 그러니까 Gradient Descent는 "Gradient의 반대 방향으로"라는 의미가 훨씬 명확하다고 생각합니다. 짜잔.
이렇게 결론부터 이야기하긴 했는데, 자세히 들여다 보지 않는 이상 이건 또 무슨 말인가. 하는 생각이 들거라 생각합니다. 자세히 들여다보면 이게 듣도보도 못한 신박한 방법이라기보다는 누구라도 그렇게 생각할 수밖에 없는 단순한 방법이라는 걸 깨닫게 될 것입니다.
그렇다면, 이제까지 다뤄왔던 가장 만만할 것만 같은 회귀를 Gradient Descent로 풀어보도록 하겠습니다.
자, 일단 회귀의 Cost함수가 머였는지 기억해 낼 수 있겠어요? 기억 못해도 쑥스러워하진 마세요. 이 함수는 아래로 볼록한 Convex 함수로써,
$$\underset{\theta}{argmin}\sum\limits_{i}^{N}{{(y_i-(\beta_0+ \beta_1{x_i}))^2}}\,where \,\theta=[\beta_0, \beta_1]$$
이거였었는데, 기억하겠지요? 후후. (Observation-Predict)²의 합, 즉 Residual 제곱합을 최소로 하는 Least Sqaure 방법이었잖아요? - Likelihood를 통해서도 이 Least Square를 증명했었었는데 기억하겠죠 -
자, 어쩄든 이 Cost가 최소인 값을 찾아가야 하는 거구요, 어떤 함수의 최소값을 구할 때에는 본능적으로 뭐가 생각나나요. 미분=0죠. Cost의 미분=0를 찾아가야 하겠는데 말이죠, 잠시 미분을 하기 전에 미분 후에 계산하기 편하게 하기 위해서 Cost를 다시 정의하면,
$$ Cost(\beta_0, \beta_1) = \cfrac{1}{2N} \sum\limits_{i}^{N}{{(y_i-(\beta_0+ \beta_1{x_i}))^2}}$$
로 정의할 수 있겠는데요, 여기에서 N은 평균을 낸거구요, 2는 이 Cost를 미분했을 때 제곱의 2가 앞으로 튀어나오니까 약분해서 간단하게 하려고 임의로 넣은 상수예요. 특별한 의미는 없으니까 신경 쓰이더라도 잊어요.
그리고, 여기에서 일단 간략하게 알아보기 위해서 β₀ 절편은 빼고요, 기울기β₁만 고려해서 들여다 본다면,
$$ Cost(\beta_1) = \cfrac{1}{2N} \sum\limits_{i}^{N}{{(y_i-( \beta_1{x_i}))^2}}$$
요런 Cost 함수가 되겠죠. 어떻게 하면 최소값을 찾아낼 수 있을까를 고민해 보시죠.
일단, 다음과 같은 데이터가 있다고 치고, 이것을 Gradient Descent - 회귀를 해 보면 확실하게 이해할 수 있어요.
자, 여기에 어떤 기울기를 가진 직선을 그어야 Cost가 가장 작아질지 탐험해 가도록 해요.
적당한 선은 β₁의 기울기를 갖는 (원점을 지나는) 추세선이 되겠고, 이것에 대한 Cost를 따져봅시다. 각 Observation에 대해서 (Observation-Predict)²을 따지는 겁니다. Cost를 다시 써보면,
$$ Cost(\beta_1) = \cfrac{1}{2N} \sum\limits_{i}^{N}{{(y_i-( \beta_1{x_i}))^2}}$$
이니까,
$\begin{align}
Cost(\beta_1) = \cfrac{1}{2\times3} ( & \\ & \,\,\,\,\, (0.45-0.5\times\beta_1)^2 \\&+ (0.95-2.3\times\beta_1)^2 \\&+ (2.25-2.9\times\beta_1)^2 \,\,\ )
\end{align} $
이런 식으로 Cost를 계산할 수 있겠죠. 근데, 잘 보면 Cost가 β₁의 2차식이 되거든요, 당연한 이야기이겠지만 β₁에 대해서 이 Cost(β₁)의 그래프를 그려보면 포물선을 그리는 2차식 그래프가 되겠습니다. 당연한 이야기인가요.
자, 여기까지 왔으면 뭔가 우리가 해야할 일이 보이지 않나요? 그렇습니다. Cost(β₁)을 β₁으로 미분했을 때 기울기가 0인 지점을 찾아낸다면! 바로 최소의 Cost 지점에서의 β₁을 찾을 수 있는 것이겠지요?
중요한 시점이 되었습니다. 이때 그 지점을 찾기 위한 기교가 Gradient Descent입니다. 이 Grandient Descent는 어떤 Arbitrary지점에서의 기울기를 구해서 그 기울기가 어떤가에 따라서 이 Cost함수의 경사를 타고 내려 올 수 있도록 하는 것입니다.
이게 무슨 의미냐 하면, 다음의 그림처럼 어떤 점에서 미분값, 즉 기울기가 음수면 어떤 의미일까요?
기울기가 음수라는 뜻은 더 오른쪽으로 가야 최소값에 가까워질 수 있다는 의미입니다. 그러니까 그런 경우에는 학습을 해감에 따라 더 오른쪽으로 이동해 가면서 최소점을 찾아갑니다.
이런 식으로 "경사"를 따라 내려가다 보면 최소값, 즉 미분값이 0인 지점에 이르게 될 수 있겠습니다.
그러면 어떤 점에서 미분값, 즉 기울기가 양수라면 어떨까요?
점점 더 왼쪽으로 이동하면 미분값이 0인 최소값에 이르게 되지 않겠습니꽈? 그것 참 단순하군요.
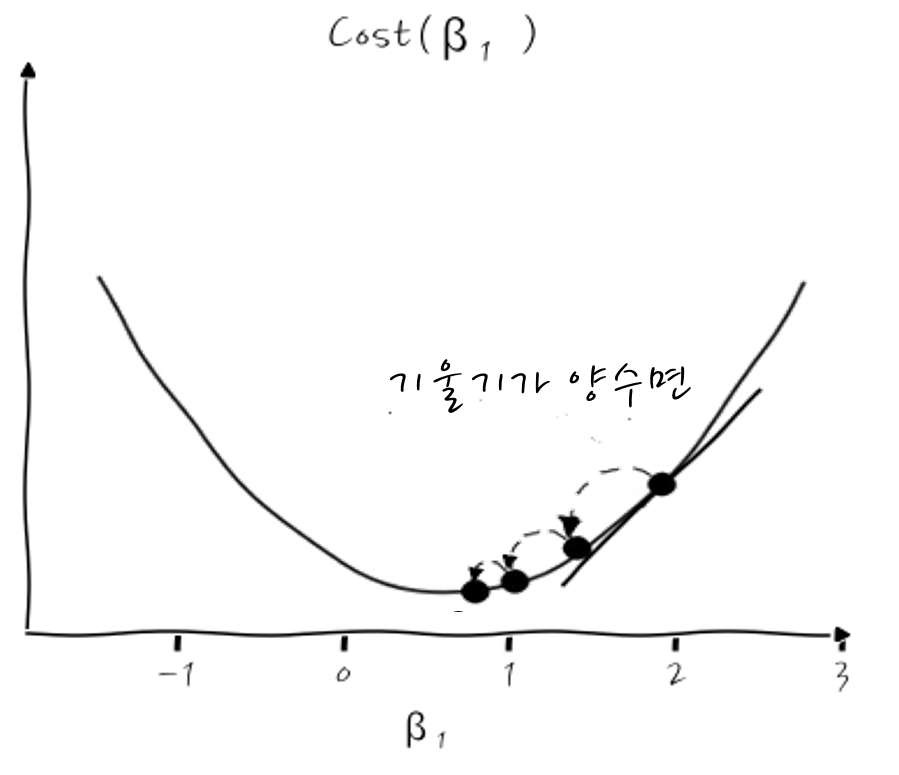
자, 그런 의미에서 말이죠, 이렇게 경사를 따라 내려갈 때마다 기울기 β₁을 새로운 β₁으로 계속 갱신을 하게 되는데 그럴 때 표현으로 x:=x 라는 표현을 씁니다. 이 Notation을 빌려 β₁의 갱신을 다시 표현해 보면,
$$ \beta_1 := \beta_1 - \eta \cfrac{\partial}{\partial \beta_1} Cost(\beta_1) $$
이런 식으로 표현하는데 이 의미는 기존의 β₁에서 기울기에 η만큼 곱해서 점점 이동해 가는 와중에 이 η값이 크면 큰 스텝으로 이동하고, η이 작으면 작은 스텝으로 이동해서 최소점을 찾아가게 될 것입니다. Cost미분의 두 번째 Term의 앞에 붙은 부호 -의 의미는 기울기가 음수이면 플러스가 되어 오른쪽으로, 기울기가 양수이면 마이너스가 되어 왼쪽으로 찾아내려 가기 위한 부호입니다. 오호. 이걸 쉽게 이해하는 방법은 Gradient의 반대 방향으로 가면 자연스럽게 경사를 따라내려오게 된다고 이해하면 마이너스 부호도 쉽게 떠올릴 수 있습니다.
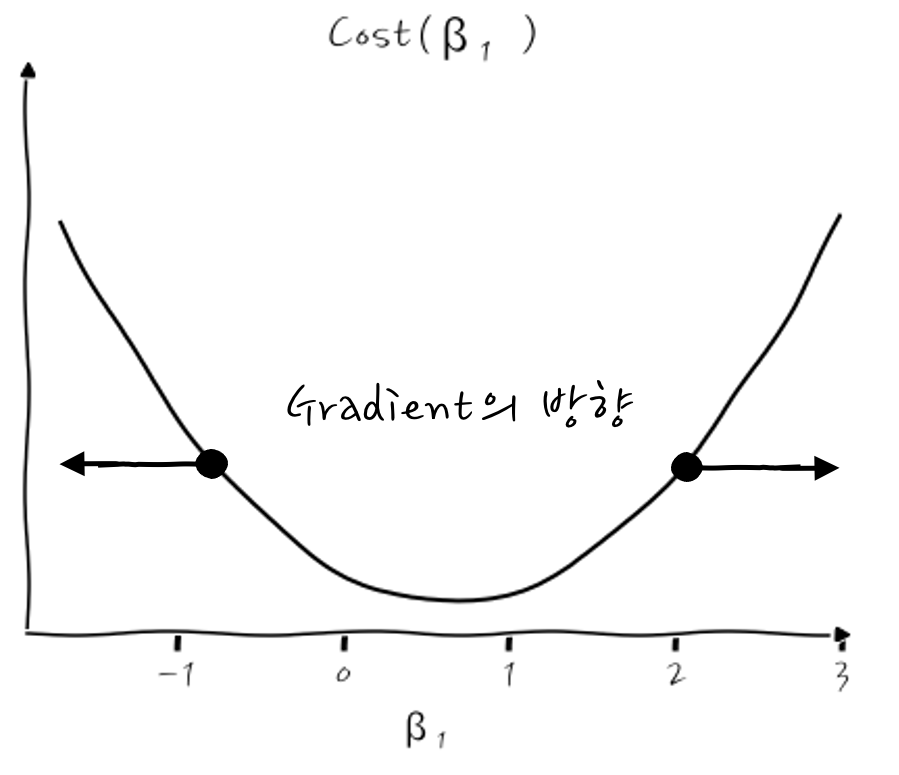
이때 η를 학습률이라고 표현하고, 학습률이 크면 더 좋고 빠른 학습을 해야 할 것 같지만, 실제로는 얼마나 큰 스텝으로 경사를 내려갈 것이냐를 의미합니다. 오해하지 마세요.
결국, 미분을 해서 β₁의 갱신식을 최종적으로 정리해 보면,
$$ \begin{align} \beta_1 &:= \beta_1 - \eta \cfrac{\partial}{\partial \beta_1} Cost(\beta_1) \\ &=\beta_1 - \eta \cfrac{\partial}{\partial \beta_1} \cfrac{1}{2N} \sum\limits_{i}^{N}{{(y_i-( \beta_1{x_i}))^2}} \\ &=\beta_1 - \eta \cfrac{1}{2N} \sum\limits_{i}^{N}{ 2(y_i-\beta_1x_i)(-x_i)} \\ &= \beta_1 - \eta \cfrac{1}{N} \sum\limits_{i}^{N}{ (y_i-\beta_1x_i)(-x_i)} \\ &= \beta_1 - \eta \cfrac{1}{N} \sum\limits_{i}^{N}{ (\beta_1x_i-y_i)x_i} \end{align}$$
요런 식으로 정리할 수 있겠습니다. 그렇다면 원래 주어진 문제로 돌아와서, 방금 derive한 것을 적용해 보게 된다면 말이죠,
$$ \beta_1 := \beta_1 - \eta \cfrac{1}{N} \sum\limits_{i}^{N}{ (\beta_1x_i-y_i)x_i} $$
β₁을 직접 갱신해 보자구요. 일단 최초 initial 포인트는 뭐 큰 의미는 없지만 기분에 따라 β₁=-1.50부터 시작해 보시죠, 학습률은 0.1로요. (η=0.1) η를 제외한 뒤쪽 term만을 계산해 보면,
$$ \begin{align} (&(-1.5\times0.5-0.45)\times0.5 \\+&(-1.5\times2.3-0.95)\times2.3\\ +& \underline{(-1.5\times2.9-2.25)\times2.9)})\\& \quad\quad\quad\quad 3 \\&= -10 \end{align}$$
이 됩니다. 여기에 학습률 0.1을 곱하면 -1이 되겠네요. 결국 새로운 β₁은 β₁: = β₁-(-1)=-1.5-(-1)=-0.5가 되겠습니다.
이때의 Cost는
$\begin{align}
Cost(-1.5) = \cfrac{1}{2\times3} ( & \\ & \,\,\,\,\, (0.45-0.5\times-1.5)^2 \\&+ (0.95-2.3\times-1.5)^2 \\&+ (2.25-2.9\times-1.5)^2 \,\,\ ) \\ = 10.73
\end{align} $
입니다.
아, 이런 식으로 계속해 나가면 되는데, 하나만 더 해보자면, 새로운 β₁이 -0.5니까,
$$ \begin{align} (&(-0.5\times0.5-0.45)\times0.5 \\+&(-0.5\times2.3-0.95)\times2.3\\ +& \underline{(-0.5\times2.9-2.25)\times2.9))}\\& \quad\quad\quad\quad 3 \\&= -5.3 \end{align}$$
여기에 학습률 0.1을 곱하면 -0.53이 됩니다.
그러니까, 결국 새로운 β₁은 β₁: = β₁-(-0.53)=0.3이 되겠습니다.
이때의 Cost는
$\begin{align}
Cost(-0.5) = \cfrac{1}{2\times3} ( & \\ & \,\,\,\,\, (0.45-0.5\times-0.5)^2 \\&+ (0.95-2.3\times-0.5)^2 \\&+ (2.25-2.9\times-0.5)^2 \,\,\ ) \\ = 3.12
\end{align} $
이제는 어떤 식으로 이야기가 흘러가는지 눈치챘을 테니까, β₁과 Cost(β₁)을 주르륵 계산해서 써 보면
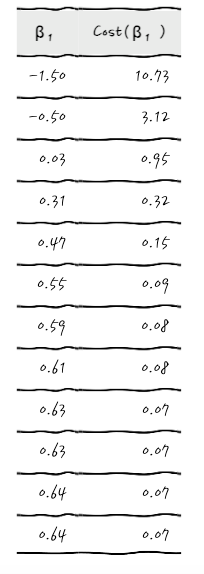
이런 식이 됩니다. 이걸 Cost(β₁) 그래프를 그려서 확인해 보면,
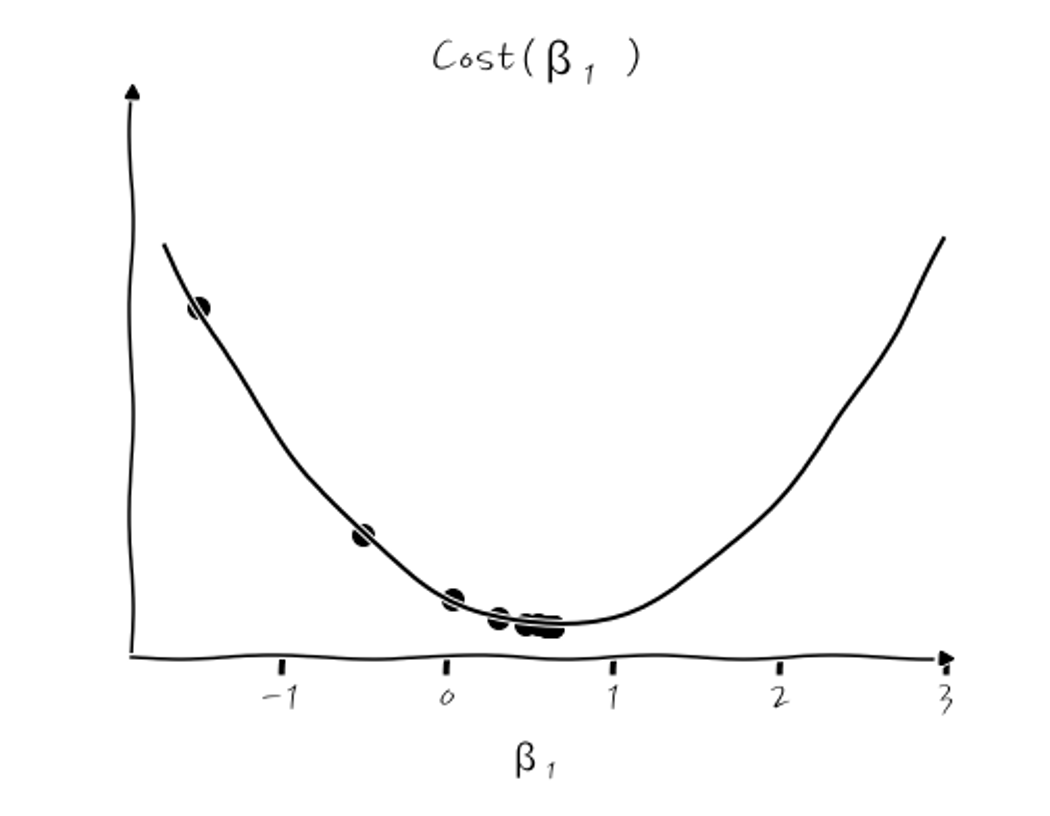
이런 식이 되는데, β₁이 초기 시작값 -1.5에서부터 극소점을 향해 계속 줄어드는 것을 확인할 수 있습니다. 실무에서는 이 Cost(β₁)이 얼마나 줄어드는지 보는 history 그래프가 많이 쓰이니까, 이걸로 본다면,
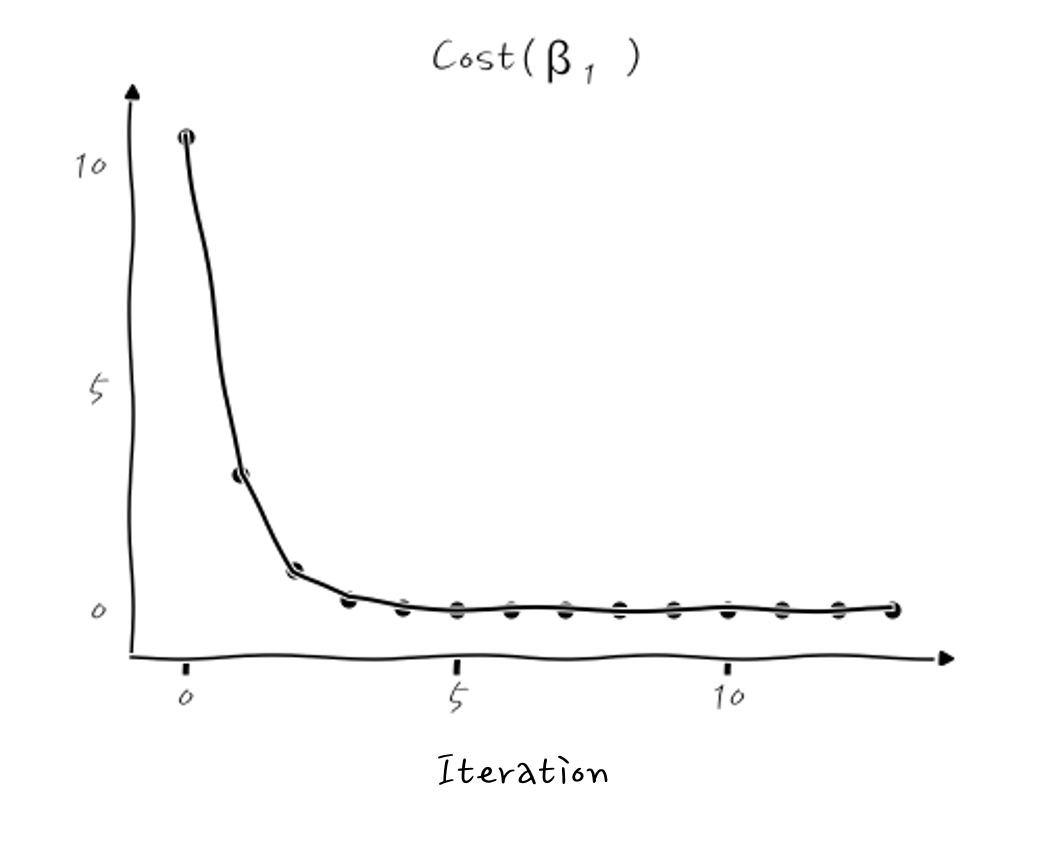
이렇게 Cost가 계속 줄어들면서 최적화가 진행되는 것을 확인할 수 있습니다. 결국, β₁이 0.64로 수렴하게 되는데, 이때의 회귀 그래프는 y=0.64x가 됩니다.
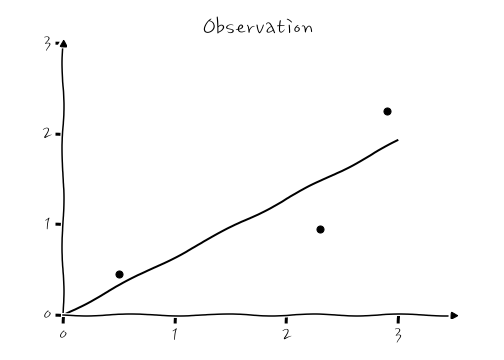
이렇게 회귀선이 학습되었습니다. 어떤가요. 대충 맞아 들어가는 것 같습니다만. 휴.
그런데 말이죠, 여기에서 굉장히 주의할 점이 있는데요, 학습률이라는 게 더 크게 극소점을 찾아가게 하는 값이라는 점에서 마음이 급한 나머지 학습률을 너무 크게 설정하면 어떤 일이 벌어지냐면 수렴하지 않고 발산합니다. 어떤 식이냐면, (η=0.5의 경우)
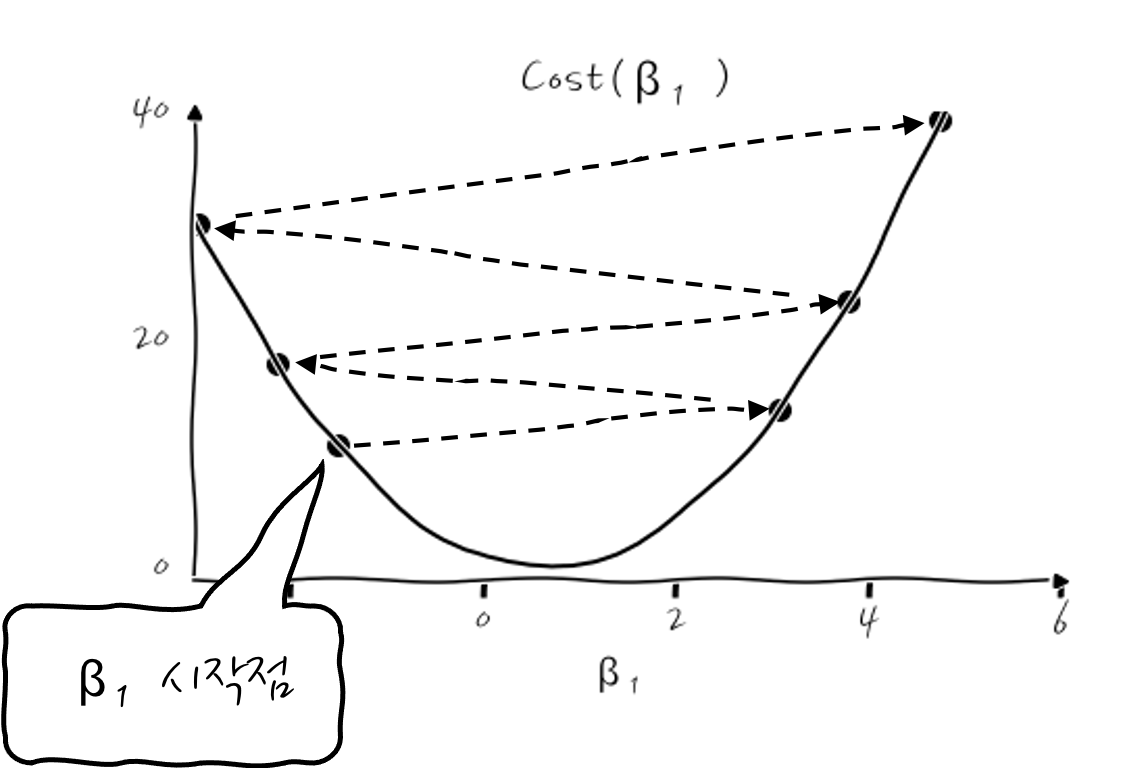
이런 식인데, 학습률이 너무 크면, 더 작은 값으로 내려가기 전에, 최소값을 그만 건너뛰고 넘어가 버려서, 점점 더 악순환을 겪게 됩니다. 이런 경우 Cost가 발산하는 것처럼 보입니다.
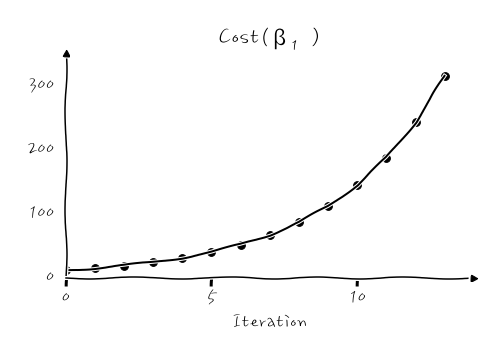
이런 식으로 줄어들지 않고 계속 커져요. 흐익.
그러면, 촘촘하게 놓치지 말아야 하겠다고 생각해서 학습률을 너무 작게 잡으면? 어떻게 될지 상상이 쉽게 되겠죠?
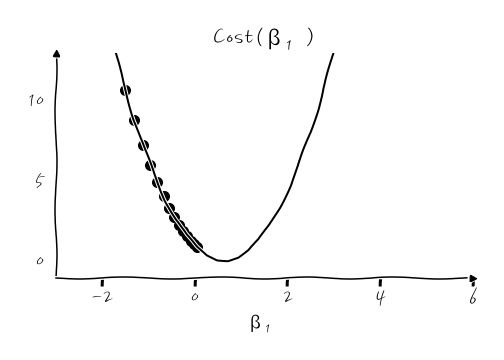
너무 촘촘하게 갱신해 나가다 보니 너무 느려집니다. 최소값을 놓치진 않겠지만 느려도 너~무 느립니다. 하세월 찾아가는데, 그러면 집에는 언제 가나요.
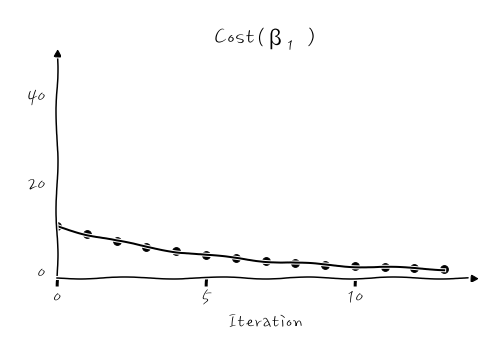
이런 식으로 찾아간다면 어느 세월에 찾아갈지 모르죠. 아마도 제가 알고 지내는 INTJ들은 이런 식으로 설정해 놓고, 서버 옆에서 밤을 새우면서 왜 이렇게 한참 걸리냐 망할 싸구려 서버하면서, 서버 탓을 하고 있을지도 모릅니다.
어쨌든 적당한 학습률을 적용하는 것도 매우 중요한 미션이 되겠습니다. (이게 Adaptive 하게 변하게 하는 방법도 있긴 있는데, 그건 혹시나 기회가 된다면 그때 다시 이야기해도 흥미로울 것 같군요.)
이런 현상이 일어난다는 것을 알고 있다면 Cost History 그래프를 보고 대충 음음 학습률이 너무 크구먼, 음~ 학습률이 너무 작구먼 하고 추리 할수 있게 될 텐데요, 그것만으로도 꽤나 이런 원리를 이해하고 있다는 느낌을 주니까, 의미가 있는 것 아닐까 생각합니다.
실제로 계산을 통해 구한 회귀방정식도 y = 0.64x거든요? 그러면 Gradient Descent를 통해서 학습한 결과도 잘 찾아냈다고 볼 수 있겠습니다.
이해를 위해서, β₀를 생략하고, 기울기만 가지고 gradient descent를 해 보았는데, β₀와 β₁을 한꺼번에 고려하면 어찌해야 할지 난감할 수도 있겠는데 라는 생각이 문득 들었습니다. 이럴 땐 두 개의 Cost를 한꺼번에 계산하면서 Gradient descent를 합니다.
β₀와 β₁을 모두 고려한 Cost(β₀, β₁)-이른 바 Sum of Squared Residual -은
$Cost(\beta_0, \beta_1) = \sum\cfrac{1}{2N}(y_i - (\beta_0+\beta_1 x_i))^2$ 이잖아요?
그러니까, 각각의 편미분을 하면,
$$\cfrac{\partial }{\partial \beta_0} Cost(\beta_0, \beta_1) = \cfrac{1}{N}\sum(\beta_0+\beta_1 x_i -y_i) \\
\cfrac{\partial }{\partial \beta_1} Cost(\beta_0, \beta_1) = \cfrac{1}{N}\sum(\beta_0+\beta_1 x_i -y_i)\,x_i$$
이 되겠군요.
그러니까, 각각의 Update 식을 따로 써 보면,
$$ \beta_0 := \beta_0 - \eta \cfrac{1}{N} \sum\limits_{i}^{N}{ ( \beta_0 + \beta_1x_i-y_i)} \\
\beta_1 := \beta_1 - \eta \cfrac{1}{N} \sum\limits_{i}^{N}{ ( \beta_0 + \beta_1x_i-y_i)x_i} $$
가 될 수 있겠는데, 요걸 이용해서 동시에 갱신해 나가면 되겠습니다. 음
예를 들어, 최초에 β₀가 0, β₁이 1이라고 한다면,
최초의 비용은 $Cost(\beta_0, \beta_1)\biggr\rvert_{\beta_0=0, \beta_1=1}=\sum\limits_{i}^{N} \cfrac{1}{2N}(0+1\cdot x_i - y_i)^2$ 이 되고요, 이 두 개의 계수에 대하여 Gradient를 계산하면 다음과 같겠습니다.
$$ \beta_0 := 0 - \eta \cfrac{1}{N} \sum\limits_{i}^{N}{ ( 0 + 1 \cdot x_i-y_i)} \\
\beta_1 := 0 - \eta \cfrac{1}{N} \sum\limits_{i}^{N}{ ( 0 + 1 \cdot x_i-y_i)x_i} $$
이런 식으로 새로운 계수들을 한꺼번에 갱신하면서 3차원 산봉우리의 가장 가파른 능선을 따라 내려오면 됩니다. 이것도 마찬가지로 Gradient의 반대방향으로 따라 내려오는 것이라는 점이 교훈입니다.
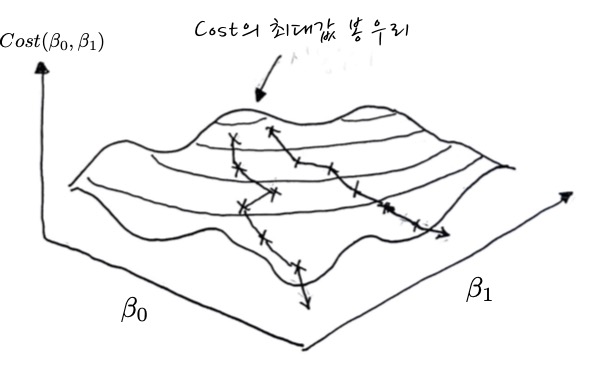
봉우리에서 내려오면서 표시되어 있는 각각의 X표는 각 계수에 대한 동시갱신 지점입니다.
뭐 어렵지 않죠?
친절한 데이터 사이언스 강좌 글 전체 목차 (정주행 링크) - 
댓글