방금 Boosting이라는 걸 Ada Boosting를 통해서 살펴봤습니다. Bagging과 다른 점은 잘못 분류한 Training Data에 더 큰 Weight를 주고서 Weighting에 따라 다시 Sampling하여 그다음 분류기를 학습시킨다는 점에서 뭔가 괜찮은 방법 같은 생각이 듭니다. 그런데, 이미 눈치챘을 수 있겠지만, 세상에는 좋기만 한 것은 없기 마련이고, Ada Boosting에는 큰 단점 하나 있는데, 바로 높은 Weight를 가진 Data가 존재할 경우 그것의 판별을 잘하려고 Weight를 크게 부여한 나머지 그 주변의 데이터들이 잘못 분류될 가능성이 크다는 것입니다. 아무래도 그렇지 않겠어요? 그래서, 이 문제를 해결해 보자 하고 달려들어서 제시한 방법이 Gradient Boosting입니다. 게다가 Gradient Boosting이야 말로 Sequential Decision Tree를 제대로 구현한 것입니다.
간단한 아이디어만 슬쩍 이야기 해 보자면, 가중치를 업데이트하는 방식을 기존의 AdaBoost에서 사용한 단순한 지수 곱셈식 방식에서 Gradient Descent(경사하강법)이라는 방식으로 바꾸었고, 통계적으로도 보다 높은 정확도를 보여주게 되었다는 풍문입니다. 어쨌든 여기저기에서 떠들썩한 Gradient Descent라는 걸 드디어 만나게 되었군요. 참고로 Gradient Boosting은 GBM이라고도 많이 부르는데, M은 Machine을 말합니다.
일단, 이게 어떤 식으로 동작하는지를 보고 나서 수학적인 접근을 보면 그 실체를 이해하기 쉬우니까 한번 보시죠. 일단 다음과 같은 데이터 세트가 있다고 합시다.
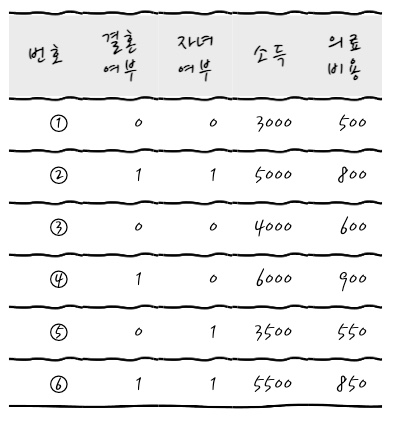
이때 목표는 의료비용이 예측하고자 하는 것입니다. 첫 번째 단계로 다짜고짜 일단 의료비용의 첫 번째 예측값을 구합니다. 그 예측값이 뭐냐면 걍 평균입니다. (회귀할 때 엉망진창 회귀선이 y의 평균이었는데 그것과 컨셉이 비슷하군요.)
이렇게 첫번째 예측값인 평균을 적어놓습니다. 여기에서 무슨 짓을 하냐면 Pseudo Residual-의사 잔차-이라는 걸 구하는데 이게 뭐냐면 실제값(정답)과 예측의 차이 (Label-Prediction)를 의미합니다. 어찌 보면 이게 Error군요.
자, 그럼 잔차를 구해서 써 넣어볼까요? 이제부터는 잔차를 계속 구할 거라서 잔차0이라고 번호를 붙이겠습니다.
그러면 이제 원래 정답인 Label과 예측값간의 차이 즉 잔차라는 것이 구해졌습니다. 이 부분이 정말 재미있는 부분인데, 결혼/자녀/소득을 가지고 이 잔차를 예측해 보도록 하겠습니다. 이 예측을 어떤 식으로 하냐면, 잔차를 Label로 해서 Decision Tree를 만들어서 하는 것입니다. Decision Tree를 만들어 보면 다음 그림과 같습니다. Tree를 통해서 뭔가 추가된 계산을 하게 되는데 그걸 살펴보면,
ⓐ 잔차를 Label로 해서 결정나무를 "만들어서" 잔차를 분류합니다. 결정나무는 잔차를 가장 잘 분리하는 방식으로 만듭니다. 이건 다른 말로 예측이라고도 할 수 있겠죠. 같은 것으로 분류된 잔차는 평균을 내서 하나의 값으로 만듭니다. 이걸 Pseudo Residual(의사잔차)라고 부릅니다. 평균을 내서 뭉뚱그렸으니까 잔차는 잔차인데 가짜 잔차입니다.
ⓑ 분류한 건 잔차니까 원래의 예측값에 잔차를 더하면 원래 예측값이 나오겠죠. 이렇게 하면 결정나무 1개로 예측한 걸로 끝이 나고 그동안 즐거웠어요~ 했으면 좋겠는데 Boosting이란 게 그게 아니지 않겠어요? 게다가 ①번 데이터의 경우를 보면 Label이 500인데, 예측치도 500입니다.(왜냐하면 700-200) 이런 경우에는 너무 Overfitting이 되게 됩니다.
ⓒ 그러니까 이런 경우에는 잔차에 Learning Rate라는 걸 곱해서 잔차의 크기를 줄여서 더합니다. 이걸 업데이트(Update)라고 부릅니다. 원래의 예측값과 업데이트를 더해서 새로운 예측치를 만듭니다. 데이터로 직접 보면,
방금 이야기를 이해하기 위해 네모 친 값을 보면, 새로운 의료비용 예측값(예측+의사잔차)와 Ground Truth인 의료비용이 똑같아서 과적합됩니다. 와우. 이런 게 바로 과적합된 상태입니다. 이 순간 예측+잔차평균(의사잔차) 열을 통해서 과적합되는 가능성을 보았으니까 이제 의사잔차에 학습률을 곱해서 업데이트를 예측할 때 씁니다. (여기에서 학습률은 0.1입니다.) 정리된 남겨서 데이터를 구성해 보면 다음과 같습니다.
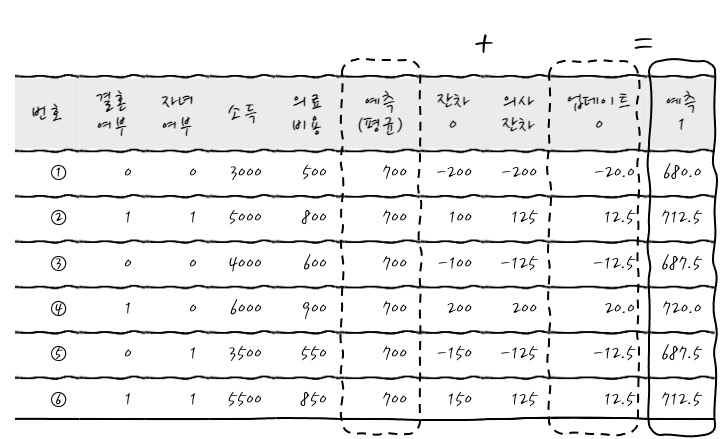
최초 예측값(Label 평균)+업데이트를 더하면 다음 예측값이 됩니다. 이렇게 첫번째 iteration이 끝이 납니다. 자, 이제 새로운 예측치가 나왔으니까 기존의 평균으로 예측했던 것을 이 예측치로 대치하고 똑같은 짓을 다시 합니다. 다시 말해 이 예측치를 통해서 다시 잔차(Label-예측치)를 계산한 후에 결정나무를 "만들어서" 이 잔차를 분류합니다. 그런 후에 잔차에 Learning rate를 곱해서 Update값을 구한 후 예측치에 이 Update를 더해서 새로운 예측치를 만듭니다. 똑같은 절차를 계속~ 하는 겁니다.
우선 잔차를 구한후에 결정나무를 통해 잔차를 예측하고 그 잔차를 의사잔차(Pseudo Residual)로 바꾼 후에 학습률을 곱한 후 더해서 다음 예측치를 구해 보겠습니다.
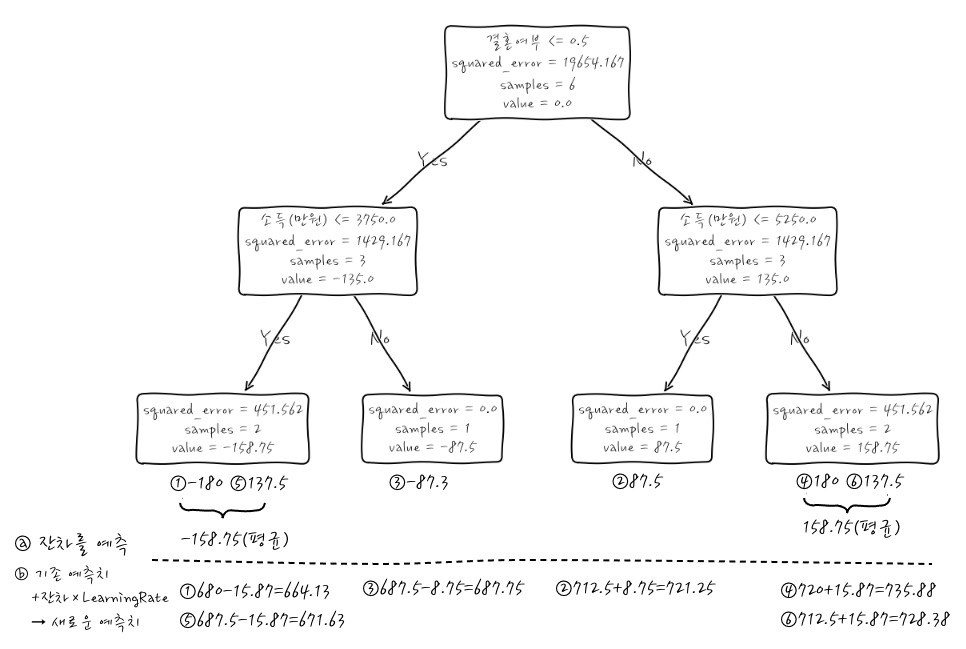
이 계산의 근거는 다음과 같습니다.
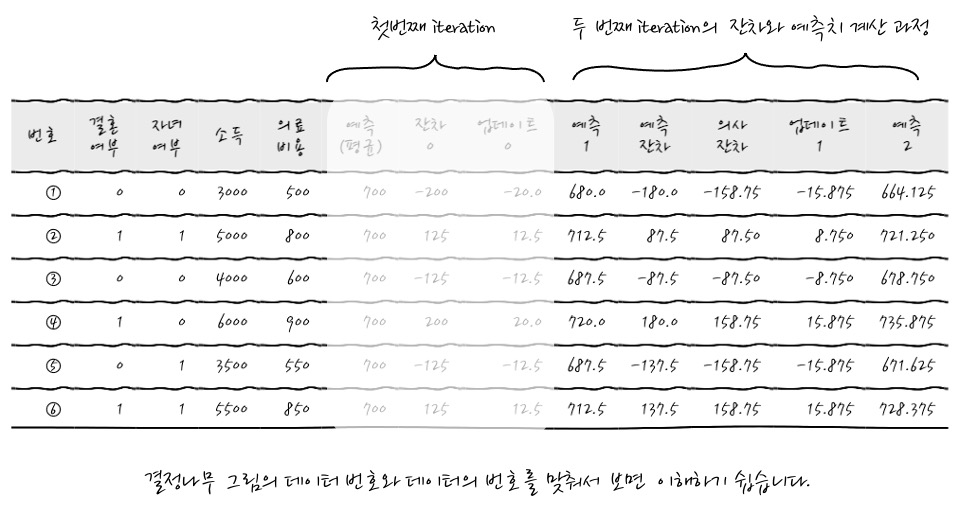
어떤가요. 이것이 두번째 iteration이라는 것입니다. 이런 식으로 계속 가다 보면 점진적으로 Error가 줄어들고 예측모형이 완성되어질 수 있습니다.
결국 모형은 이런 식으로 생긴겁니다. 정리해 보면 학습은
① 초기 예측값 설정: 보통 타겟 변수의 평균값을 사용합니다
② 계속 트리를 추가해 가면서 새로운 트리 학습:
- 현재 예측값과 실제 값의 차이(잔차)를 계산합니다.
- 이 잔차를 타겟으로 하여 결정 트리를 학습시킵니다.
- 잔차와 학습률을 곱한 업데이트값을 구하여 기존 예측값을 더하여 새로운 예측값을 내놓습니다.
③ 결국, 이걸 반복하면 학습된 트리들은 잔차를 예측하는 모델이 됩니다.
그러면, 예측은 어떻게 하는 것일까요? 방금 학습에서 보았듯이 학습된 트리들은 잔차를 예측합니다.
① 초기 예측값으로 시작합니다 (타겟 변수의 평균
② 각 트리에서 잔차를 예측합니다.
③ 예측된 잔차에 학습률을 곱합니다.
④ 이 값들을 모두 더해 초기 예측값에 더합니다.
각 트리들은 잔차들을 예측한거니까 더해가다 보면 최종 예측치를 구할 수 있겠습니다.
뭐 학습하면서 Tree들을 만들어내면,
요런 느낌적인 느낌으로 순차적으로 모형을 보강해서 최종 결과를 낸다는 느낌입니다.
휴우, 한참 어떤 식으로 동작하는지를 보긴 봤는데 아니, 이게 왜 Gradient Descent방법을 사용한 Boosting이냐?? 싶을 텐데, 이것을 수식적으로 설명하고 넘어가야 속이 시원하겠습니다.
이게 Gradient Descent는 보통 Loss function을 줄이기 위해서 사용하게 되는데, 그 스토리를 이야기 해 보자면, Loss는 당연히 실제 Ground Truth와 예측값의 차이를 Loss로 두잖아요? 미분을 편하게 하기 위하여 Loss를 차이의 제곱으로 두면, 다음과 같습니다. - 차이의 제곱으로 둬야 미분해서 최솟값을 구할 수 있습니다, 그리고 y가 Ground Truth, p가 predict로 두면 -
Loss=12∑(actual−predict)2=12∑(y−p)2
그러면 예측에 대한 Loss의 미분, 즉 Gradient는 다음과 같이 표현할 수 있겠습니다.
Loss′=∂L∂p=−(y−p)=Residual
오호, 이걸 보니 어때요? y-p가 뭐였죠? 흐헙! 잔차였지 않습니꺄? 아하하. 그러니까, Loss를 줄여가는 방향은 잔차를 줄여가는 방향이라는 뜻입니다. 하하. 약간 저릿하군요.
그러니까 최적화 과정에서 손실함수를 최소화 하는 방향으로 움직여야 하니까,
p←p−η⋅∂L∂p
로 움직이게 됩니다. η는 이미 보았듯이 학습률입니다. 그러면 잔차가 Loss인걸 알았고, 전체적인 스토리를 보면,
모델은 반복적으로 업데이트되며, 각 단계에서 이전 모델의 예측 오차를 보정하는 새로운 약한 학습기를 추가합니다. 이때 학습률 η를 적용하여 업데이트의 크기를 조절합니다.
m이 현재, m-1이 이전 모델이라고 생각하고, hm(x)는 현재 모델에서의 잔차라고 생각하면 다음과 같이 표현할 수도 있겠습니다.
Fm(x)=Fm−1(x)+η⋅hm(x)
이렇듯 Loss를 실제값과 예측값의 차이의 제곱으로 정의하면 Loss의 미분이 잔차니까, 이것을 구현하는 것은 잔차를 예측하고 잔차의 차이에 대하여 학습률만큼 계속 보정해 나간다는 뭐 그런 이야기입니다.
의사결정나무를 sklearn을 이용해서 그려보면 다음과 같이
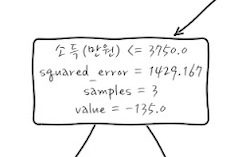
복잡한 node가 생기는데, 각 라인의 정보를 순서대로 이야기 하자면, 분기조건, 현재 node의 Error, node까지 도달한 표본수, 그때의 값을 의미합니다. 어렵게 생각하지 마세요.
친절한 데이터 사이언스 강좌 글 전체 목차 (정주행 링크) - 
댓글