Logistic Regression을 했으니까 곧바로 Logistic Classification을 다뤄보는 이야기.
사실 Logistic Regression이 어차피 확률로 1, 0을 회귀분석 하는 것이라면, Logistic Classification은 뭐가 다른가? 하는 생각이 들 텐데, 명확하게 얘기하면 Logistic Regression은 확률 회귀선의 회귀식을 구한 후 그 결과를 이용하여 각 독립변수의 영향력을 분석하는 것이 목적이고요, Classification은 분류 예측에 가깝죠.
이때, 이 모형에 어떤 Decision Rule을 적용한 후, Logistic Regression의 확률을 이용하여 분류를 할 수 있겠는데, 요 Decision Rule이라는게 분류를 위한 결정경계 즉, 1, 0을 구분하는 Decision Boundary를 고려하는 걸 말합니다. 요걸 기준으로 Classification을 해 보죠. Logistic Classification은 1/0만 구분하니까 Binary Classification이라고도 부르기도 합니다.
보통 상식적으로 1, 0을 구분하기 위해 Decision Boundary를 중간지점, 즉 확률이 0.5 지점으로 잡는데 말이죠. 0을 좀더 놓치더라도 1을 꼭 잡아내야 하면 0.3 뭐 이렇게도 하기도 합니다.
일단, 일반적인 Logistic Classification을 봅시다.
이때 어떤 임의의 Threshold를 정하고, Threshold보다 높으면 1, Threshold보다 낮으면 0으로 판단하는 논리인데요, Threshold를 0.5 즉, 1/2로 본다면 Logistic Regression 회귀식 $P = \cfrac{1}{1+e^{-(b_0+b_1 x)}} $에서 $(b_0 + b_1x)=0$이 되면 P=1/2가 됩니다. 그러니까, $x = -\cfrac{b_0}{b_1}$ 보다 오른쪽에 있으면 1, 왼쪽에 있으면 0으로 판단하는 것과 같은 이야기입니다.
이런 식이죠. 이럴 때, $-b_0 + b_1 x$ 를 0으로 만드는 $x=-\cfrac{b_0}{b_1}$ 직선을 Decision Boundary결정경계라고 합니다. 그러니까, 이 직선을 중심으로 오른쪽이면 1, 왼쪽이면 0 뭐 이런 식으로 결정할 수 있게 되는 것입니다. 호, 간단한 결정 Rule이 생겼군요.
자, 그럼 조금 더 복잡한 경우를 다뤄보면, 여러개의 Feature가 있을 때 어떻게 해야 하는가도 표현할 수 있습니다.
$P = \cfrac{1}{1+ e^{-\left(b_{0}+b_{1} x_{1}+\cdots+b_{j} x_{j}+\cdots+b_{i} x_{i}\right)}}$ 에서 $b_{0}+b_{1} x_{1}+\cdots+b_{j} x_{j} = 0$ 가 되면, threshold는 P=1/2가 됩니다. $P = \cfrac{1}{1+ e^0} = \cfrac{1}{2}$이니까요. 결정경계라는 게 이런 식으로 결정됩니다.
그럼 이해를 돕기위해, 가장 간단한 예로 2개의 Feature가 있는 경우 즉, $ b_0 + b_1x_1 + b_2x_2 = 0 $ 를 생각해 보도록 하시죠, x₁과 x₂의 분포가 다음과 같다면요,
요런 데이터 분포에서 직선을 그어서 두 개의 class를 구분하려면, 어떻게 선을 그어야 x₁과 x₂를 구분할 수 있을까요? 마찬가지로 $b_0 + b_1 x_1 + b_2 x_2 = 0$ 인 선을 그으면 로짓이 0이니까 확률이 1/2인 선이 됩니다. 그러니까 x₂를 세로축으로 하여 정리하면
$x_2 = -\cfrac{b_1}{b_2}x_1 - \cfrac{b_0}{b_2}$ 직선이 바로 그 직선이 되겠습니다.
예를 들어, $b_0=-3, b_1=1, b_2 = 1 $인 경우라면 $x_2 = -x_1 +3 $을 경계로 하고요, 이 상태의 Decision Boundary를 그려 보면요,
이런 식의 Decision Boundary가 생깁니다. 이 Decision Boundary에서 어떻게 Class를 판단하느냐? 하면
$ b_0 + b_1 x_1 + b_2 x_2 \geq 0 → P \geq 1/2 → y=1 $
$ b_0 + b_1 x_1 + b_2 x_2 < 0 → P < 1/2 → y=0 $
이 같은 Decision Boundary를 설정하여 확률이 0.5를 기준으로 1, 0을 구분할 수 있겠죠.
멋지진 않지만, x₁, x₂의 2차원에 대한 Logisitic 회귀가 실제로는 이런 식으로 생겼습니다.
요기에서 두 x에 대한 평면에 있는 $ b_0 + b_1 x_1 + b_2 x_2 = 0 $ 직선이 확률세로축(z축)으로 쭈욱~ 벽처럼 서게 되면, 이 평면이 Decision Boudary이라고 부르는 결정 경계가 되겠습니다. 자, 보세요.
이게 위에서 보면 아까 봤던 x₁, x₂의 데이터 분포와 결정경계입니다. 흡. 뭐 이런 식으로 이 평면이 가르는 곳에서 1과 0의 운명이 갈리는 평면이 되는 것입니다.
이런 경우에 Logit을 단순회귀로 풀 수도 있겠지만, Polynomial로 할 수도 있습니다. 무슨 이야기냐면 Logistic 함수에서의 Logit을 여러가지 형태로 둘 수 있다는 말인데, Logit(x)를 다음과 같이 변형할 수 있습니다.
⓵ 단순직선
$$\cfrac{1}{1+e^{-(b_0 + b_1 x_1 + b_2 x_2)}}$$
⓶ 2차식 곡선
$$\cfrac{1}{1+e^{-(b_0 + b_1 x_1 + b_2 x_2 + b_3 x_1 ^2 + b_4 x_2 ^2 + b_5 x_1 x_2)}}$$
⓷ n차식 곡선
$$\cfrac{1}{1+e^{-(b_0 + b_1 x_1 + b_2 x_1 ^2 + b_3 x_1 ^2 x_2 + b_4 x_1 ^2 x_2 ^2 \cdots)}}$$
이런 식으로 Logit을 비선형으로 표현할 수도 있습니다. 아 눈 아파. $ S(z) = \cfrac{1}{1+e^{-z}} $ 라고 정의하고 1/2인 z=0인 선을 그림으로 표현해 보면,
이런 식으로 Logit을 Polynomial로 표현할 수도 있겠습니다. 심지어는 Decision Boudary가 원으로도 가능합니다. 힉?
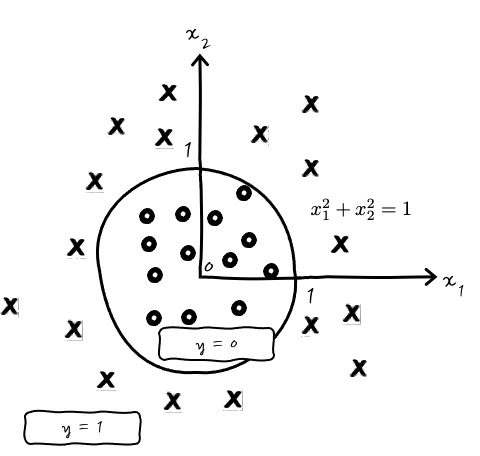
$$ y = \cfrac{1}{1+e^{-(x_1 ^2 + x_2 ^2 - 1)}} $$ 이런 식이면 반지름이 1인 원의 바깥과 안쪽으로 결정경계를 그릴 수도 있겠군요. 결정 경계가 다양하군요.
그러면 이런 결정경계 이야기를 실컷 했으니까 이번에는 종속변수가 다중클래스인 경우에 Classification을 어떻게 할 수 있는지에 대한 이야기를 지나칠 수 없겠군요. 와웃. 예를 들어 3개 class가 있다고 하시죠.
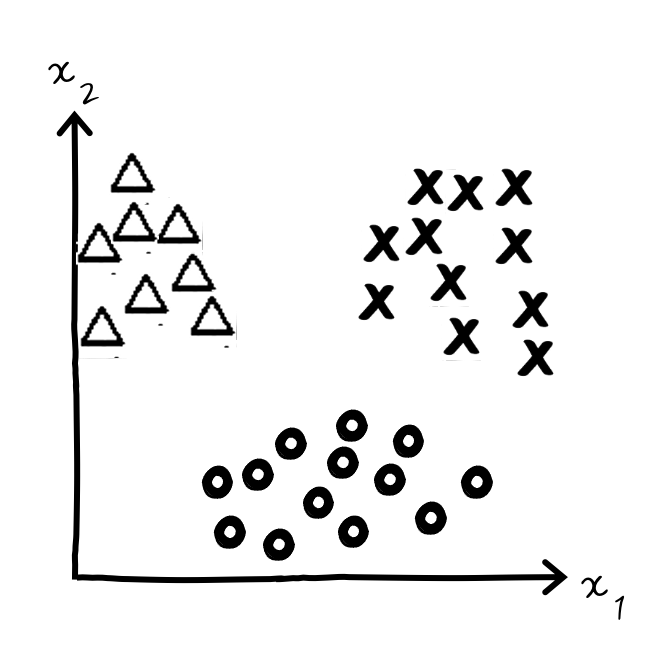
이걸 어떻게 구분한다? 하고 고민을 복잡하게 생각할 것이 아니라 Decision Boundary를 기준으로 생각하면 훨씬 간단하게 생각할 수 있습니다.
그냥 1개 클래스와 나머지 클래스를 묶어서 2개 클래스를 나누듯이 여러 번 나누면 됩니다. 보세요.
어때요? 이런 경우라면 3번을 시행할 수 있겠습니다. 종속변수가 Multi Class인 경우에는 Logisitc 회귀를 두 개씩 짝지은 만큼 시행하는 건데요. 그럼 판단은 어떤 식으로 하느냐 하면 어떤 새로운 입력값 x가 있을 때 x에 대해 이 3번의 시행 후 나오는 경우 중 가장 높은 확률이 나온 클래스를 선택합니다.
흠. 그렇긴 합니다만, 이게 쫌.. 글쵸? 그래서 조금만 더 나아가다 보면 이런 Multi Classification을 한방에 해결할 수 있는 Softmax라는 걸 다루게 됩니다. 조금만 기다려 주세요.
이야기하다 보니 좀 길어지긴 했는데 비로소 분류를 다룰 수 있게 되었습니다. 도대체 Logistic 회귀로부터 분류는 어떻게 하게 되는가? 가 궁금했다면 조금은 해소되었길 바라는 바입니다.
미리 이야기를 조금 해 두자면, 단층신경망(로지스틱회귀)으로 분류 문제를 풀 수 있는가 없는가?를 판단할 때에는 시각화한 후에 Decision Boundary를 그릴 수 있는가 없는가로 판단할 수 있겠습니다. XOR문제 같은 경우에는 단순하게 Boundary를 그릴 수 없기 때문에 다층신경망을 이용해서 공간을 Non Linear 하게 뒤틀어 버린 후에 Classification을 하게 됩니다.
친절한 데이터 사이언스 강좌 글 전체 목차 (정주행 링크) - 
댓글