혹시 신경망을 잘 모른다면 이 글은 나중에 읽었으면 좋겠습니다. 왜냐하면 이번 이야기는 신경망을 이용하는 이야기이기 때문에 지금까지 순서대로 착착 읽어 왔어도 이해하기 어려울 수 있습니다. 다만, 이미 신경망에 익숙하고, Transformer등에 관심이 있었다면야 도움이 되지 않을까 생각합니다. 그러니까, 이번 이야기는 굳이 도전!이라는 마음으로 읽어보고 싶다면 슬슬 읽어보고 넘어가고 혹시나 나중에 Attention을 문득 만나게 되면 그때 다시 읽어봐도 좋지 않을까 생각합니다. 괜히 도전!이라는 마음으로 읽었다가 더 뒤로 나아가지 못할 수 있으니까 그런 게 있었구나 정도로 마음을 먹는 편이 여러모로 행복의 지름길이 되겠습니다.
어쨌든 바로 전에 Similiarity에서 Dot Product를 다뤘기 때문에 조금 어렵더라도 신경망을 통해서 유사도를 증폭할 수 있도록 학습하는 것을 그냥 넘어가기는 제 동생이 방구를 뀌었을 때 죽빵을 날리지 않고 넘어가는 것보다 어렵기 때문에 지금 굳이 하게 되는 이야기입니다.
일단 Attention을 처음 맞닥트릴 때에는 RNN, Seq2Seq, Transformer 모형의 진화를 다루면서 Attention을 섞어 설명하는 것이 일반적인 대다수의 설명이기 때문에 처음에는 상당히 이해하기 어렵습니다. 아니 이게 뭐지 싶은데, Attention 자체를 이해하게 되면, 각 모형이 Evolution 할 때 Attention을 어떤 식으로 적용하고, 이용했는가에 대한 이해도가 높아집니다. Attention이 무엇인지만 다뤄보고 그런 이야기는 필요할 때 다시 하도록 해요.
Attention이 나올 때는 언제나 Query, Key, Value라는 것이 나오는데, 이것들이 뭔지에 대한 이해가 없으면 Attention 자체를 이해하기도 어려울뿐더러 더 나아가 RNN, Seq2Seq, Transformer를 이해하는 데에도 많은 걸림돌이 됩니다. 그러니까 이 Q(uery), K(eys), V(alues)들을 자~알 이해해야 합니다.
일단 이 3개의 term은 DB의 Metaphor에서 가져온 것입니다. DB를 예를 들면, Query는 우리가 검색을 하기 위해서 질의를 하는 것입니다. Key는 DB에서 Query를 통해 찾아낼 Index 데이터와 같습니다. 그러니까, Query는 질의하고자 하는 데이터, Key는 Query와 비교하고자 하는 대상, Value는 그때의 적절한 값을 의미합니다. 그러니까, 일반적인 Query, Key 그리고 Value의 의미는

이런 식인데요, 마지막의 Value가 엄청 이 Attention을 이해할 때 헷갈리게 하는데 말이죠, 왜냐하면 Query에 맞는 Key를 찾아내면 그 Key에 맞는 뭔가가 구해져야 하는 것이라는 생각이 들고, 그러니까 뭔가 Value는 어떤 값(Scalar 느낌?)이어야 하는 것 아닌가? 하는 그런 생각이 들기 마련인데, 이런 DB와 똑같은 메커니즘으로 이해하려고 하면 이해하기 어렵고 어색합니다. 도대체 Value는 왜 그렇게 정하는 거지? 에서 막히거든요.
어쨌든 이런 걸 자연스럽게 이해하기 위해서 하는 이야기니까 걱정은 안드로메다로 보내주세요. Attention에서는 어떤 Query를 넣으면 Query와 가장 비슷한 Key를 찾고 싶은데, 이걸 신경망으로 해결한다고 생각하면 조금 접근이 낫지 싶은데요, Attention이 동작하는 것을 순서대로 착착 들여다보시죠.
시작점으로 Query와 Key의 관계를 알아볼 때, 얼마나 서로 비슷한지를 알아낼 건데, 어떤 식으로 알아보는 것이 제일 쉽냐면, Dot Product입니다. 바로 이전 강좌에서 살펴 보았던 대로, Query를 가지고 Key중에 어떤 게 제일 비슷한가를 찾을 거니까요.
자, 보세요.

Query와 Key들 사이의 유사도를 구하기 위해서, Query Vector와 Key Vector들에 대해서 각각의 ① Query와 Key들을 Dot Product를 하면 유사도들이 나오겠죠. 오, 간단. 그리고 Dot Product를 하고 나면 얼마나 Query와 Key가 비슷한지 ② Scalar가 나오잖아요? 이것들이 각각의 Key에 대해서 ③ 유사도 값들이 있을 테죠. 여기까지는 너무나 당연한 이야기입니다.
이제 유사도 강도들을 각각의 원래 Key Vector의 크기를 조정하는 데 사용합니다. 이게 무슨 말이냐면 Key Vector에 유사도 Scalar배를 하는 거죠. 더 비슷한 Key Vector에 큰 가중치를 주는 겁니다. 어떻게요?
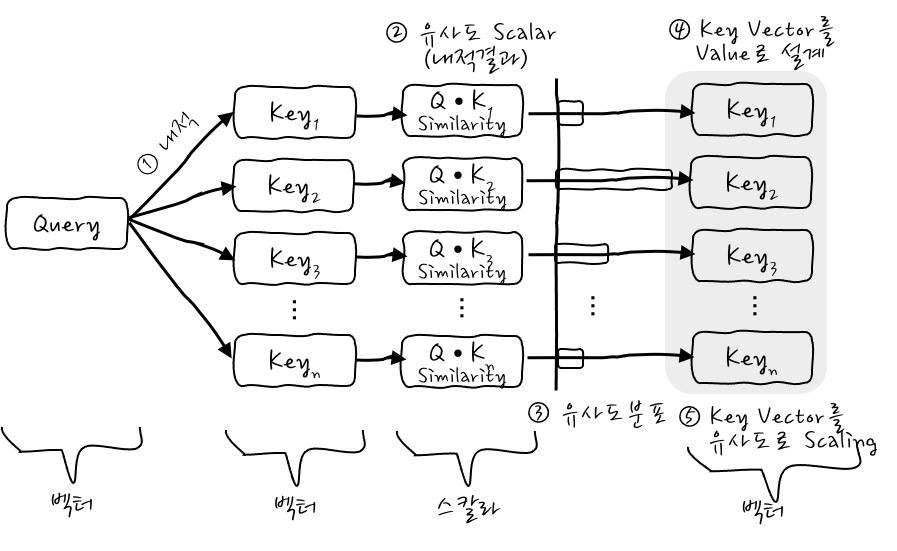
Query•Keys의 Scalar 유사도의 크기를 이용해서 각각의 자신의 Key 벡터들에 곱하면 각각의 Key 벡터가 유사도만큼 커질 수 있으니까 ④ 그때의 Value를 Key벡터로 두면 각각의 Key벡터들이 Scalar 유사도만큼의 ⑤ 가중치를 가진 Key 벡터들이 나오게 되는 거죠! 오흥? Value를 Key Vector로 설계하면, Query와 각 Key의 유사도만큼 강조한 새로운 Key벡터를 벡터공간에 나타낼 수 있습니다. 아하하하. 이 부분이 가장 중요합니다.

결국, 이런 식으로 Weighted Key Vector들을 구할 수가 있겠습니다. 이 Weighted Key를 다 더하면 Weighted Key Vector Sum이 되게 되는데 이 합 Vector에게는 가장 가중치가 큰 Vector가 제일 큰 영향을 미치겠죠. 머.

다 더한다는 건 이런 식이 되는 건데요, 더해서 Weighted Key Vector Sum Vector를 구하게 되는데 이게 Attention의 가장 중요한 메커니즘 1단계입니다. 별건 없죠?
이제까지의 그림이 가로로 너무 길어졌으니까, 압축해서 Query-Key-Value이 형태로 다시 한번 그려보자면,

이렇게 해서 마지막에 Weighted Key Vector Sum Vector를 구했는데요, 그래서 어쨌다는 말인가요, 싶은데 여기에서 가장 중요한 점은 어떤 Query가 있을 때 Key와 Dot Product 한 결과 벡터 중에 어느 것이 가장 중요한지를 스스로 학습할 수 있게 하는 것이 Attention입니다. Attention 메커니즘은 모형 니가 어떤 Key에 더 집중해야 하는지 알아서 찾아내라 뭐 그런 겁니다. 그럼 신경망을 붙이고 학습이라는 걸 시켜봐야 하겠죠! 띠용. 와웃!

어떤 Query를 넣었을 때 어떤 특정 Label이 나와야 할 경우에, 신경망을 붙이게 되면 어떤 일이 벌어지느냐 하면, Weighted Key Vector Sum Vector를 어떤 식으로 변환하면 정답 Label을 맞추기 위한 Loss가 최소가 될 것인지를 찾아내는 것입니다. 이 말은 곧 어떤 Query가 들어왔을 때 어떤 Key를 더 강조하면 Label을 잘 맞출 수 있는가와 같은 말입니다. 헛! 그렇군요.
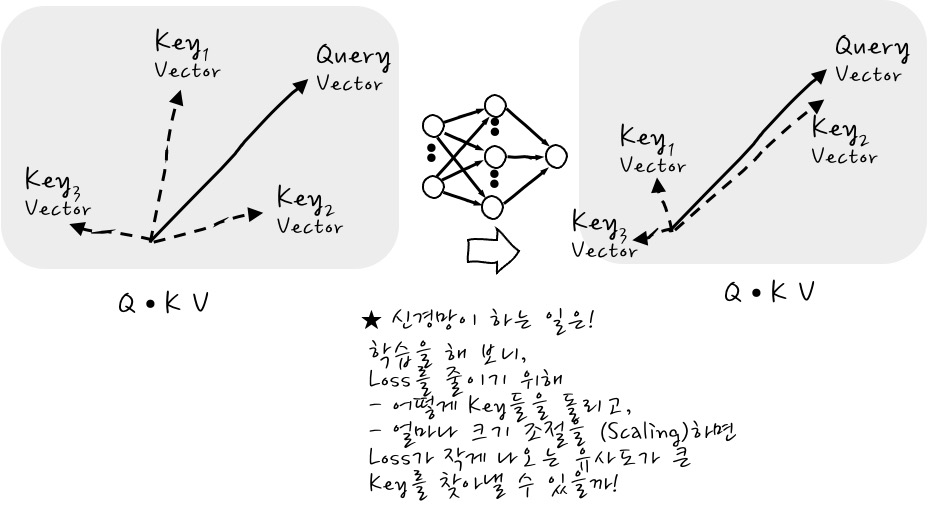
예를 들어, 신경망이 하는 일이 어떤 Query에 대해서, Loss를 줄이다 보니, 어떤 Key가 Query와의 유사도가 커지게 할 때 Loss가 작더라 그러니까 Query와 유사도가 크도록 Key 벡터들을 Rotation 하고 Scaling 하여 그 찾아낸 Key에 더 가중치를 줄 수 있을까를 찾아내는 것인데, 이것이 Attention 신경망을 학습하는 것의 의미입니다. 그림의 예시에서는 Key₂가 되겠군요.
조금 더 다듬어서 이야기하자면, Loss를 줄이기에 가장 용이한 Key Vector가 무엇일까를 찾는 과정입니다. Query의 입장에서 어떤 Key Vector를 중요하게 생각해야 Loss를 가장 줄일 수 있을까를 찾아내는 과정이 학습인 것이죠.
결국, 신경망이 학습을 완료하면 어느 Key에 제일 관심을 가져야 할지를 예츠으으윽 할 수 있게 된다!입니다. 놀랍지요?
그러면, 이제는 흔하디 흔하게 쓰이는 (Scaled) Dot Product Attention의 수식을 한번 들어야 보시죠.
$$Attention(Q,K,V) = softmax\left(\cfrac{QK^T}{\sqrt{d_K}}\right)V$$
이 수식을 보면 뭔가 Query에 Key를 내적 한 후에 이 내적 결과를 Softmax를 취해서 뭔가 크기를 줄인 다음에 그 값에 Value를 곱하는 건가? 라는 정도의 해석은 되잖아요? 지금까지 봤으니까 이 수식을 명확하게 해석하면,
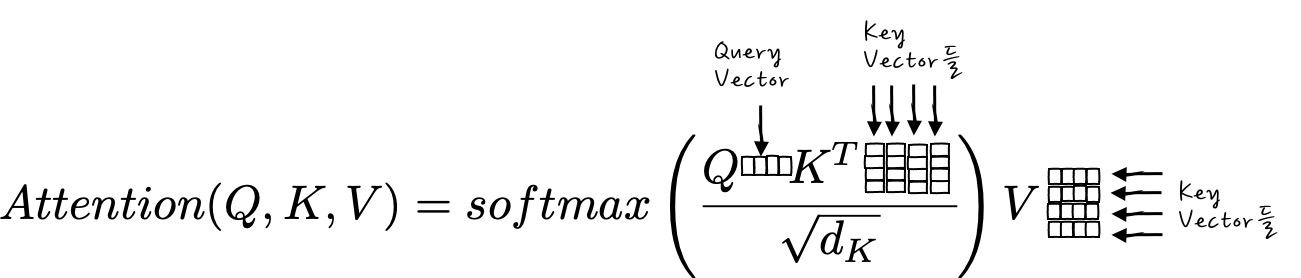
Query Vector와 Key Vector들을 내적한 후에 이걸 Key의 (Dimension으로 나눈 후에.. 이건 걍 크기 정규화라고 생각하면 됩니다.) Softmax를 취했으니까 유사도 분포를 합이 1인 가중치로 만들 수가 있는데, 이 가중치를 각각 곱해서 Weight Key 크기의 행렬을 만든 후에 Key Vector들을 각 자리마다 Weighted Key 크기를 곱한 후 합친 것이 Attention이라는 겁니다. - 조금 더 큰 의미로 정리해 보면, Attention은 주어진 Query에 대해서 모든 Key와의 유사도를 각각 구해내고, 구해낸 유사도를 각각의 Value를 Weighting 합니다. - 하하. 뭐 이제 보니까 별게 아니죠?
그러면 가장 간단한 Attention을 한번 경험해 보시죠.
지금 해보려는 걸 설명해 보자면,
5자리의 Query 벡터들이 있습니다. 이때 Query의 3번 자리가 1일 때, 신경망의 출력 Label도 1입니다. 그 외에는 출력 Label이 0입니다. 이때 과연 Attention 네트워크는 3번 자리에 더 큰 가중치를 주고 더 중요하게 생각할까를 보는 것입니다.
쉽게 이야기하면 query가
$[x_0 \,x_1 \,x_2 \, x_3\, x_4]$ 의 다섯 자리 벡터라고 했을 때,
$[x_0 \,x_1 \,x_2 \, 1, x_4]$ 이면, 3번 자리가 1이면, Label이 1
$[x_0 \,x_1 \,x_2 \, 0, x_4]$ 이면, 3번 자리가 0이면, Label이 0
이런 것을 학습시켜서 3번 자리에 제대로 신경망이 Attention을 하는지 보겠다는 뭐 그런 이야기입니다. 4번째 자리이지만 x가 0부터 시작하니까, 4번째 자리는 3번 자리입니다. 주의해 주세요. 헷갈림 방지를 위해 3번 자리라고 통일해서 부르겠습니다.
자, 그럼 이 Attention 신경망을 설계해 봅시다.
① Query는 5자리 벡터들 일거구요, 여기에서 할 일은 Query와 무엇의 유사도를 보면 되는가?인데,
② 이때 Key 벡터는 2개를 두는데, 하나는 query와 같고, 하나는 key의 0번째 자리가 query의 1/0과 같습니다.
표로 보면 이런 식의 데이터인데요,
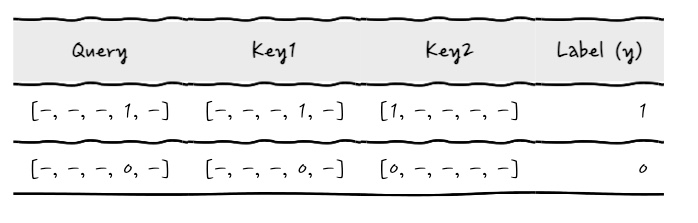
- 딱 Query•Key₁의 내적이 크게 나와야 할 것 같지 않나요? 조금 더 현실감을 주기 위해서 실제 모형에서는 Key₁과 Key₂에 Softmax를 주어서 1보다는 작은 값으로 만들어서 해볼 겁니다.. -
③ 그랬을 때, Value 벡터는 각각의 Key 벡터가 되도록 하고, 모든 QKV를 합하면 5자리 벡터가 나옵니다.
④ 마지막에 QKV Sum Vector이 크기인 5개 입력, 1개 출력인 신경망을 두는데, Hidden Layer는 크게 한번 해 보죠 머. 입력의 4배 정도 되는 20 노드의 Hidden Layer를 두면 충분하지 않을까 합니다. - 여기에서 4배는 꼭 그렇게 해야 한다는 의미가 아니라 걍 그 정도 둔 겁니다. 아마도 더 많으면 좋을 거라 생각합니다. 많으면 많을수록 학습해야 할 parameter는 많아지지만, 출력의 분포를 더 잘 표현할 수 있으니까요 -
④ Loss는 출력이 1/0이니까, Binary Claasification으로 생각하고 Binary Cross Entropy로 놓으면 되겠고요.
⑤ Optimizer는 Adam으로 두면 어느 정도 괜찮지 않을까 생각합니다. (왜 Adam을선택했는가 하는 문제는 신경망을 다룰 때 다시 이야기하도록 해요)
자, 이제 구현을 한번 해봅시다. 필요한 것들을 import 해 주고요.
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import models
from tensorflow.keras import layers
from tensorflow.keras import backend as K
import numpy as np
import pandas as pd
일단, Query와 Label을 만들어 봅시다.
data_size = 1000 # 전체 데이터 크기
input_dims = 5 # 데이터 차원 (5 Size 벡터)
attention_column = 3 # 3번자리 요소에 Attention 될테니까
def build_data(data_size, input_size, attention_index) :
train_x = np.random.standard_normal(size=(data_size, input_size))
train_y = np.random.randint(low=0, high=2, size=(batch_size,1))
train_x[:, attention_index] = train_y[:, 0] # y가 1인 경우에는 query의 3번 컬럼을 1로 세팅
return (train_x, train_y)
# 훈련 데이터 만들기
train_x, train_y = build_data(data_size, input_dims, attention_column)
이렇게 하면 랜덤 5자리 데이터를 1000개를 만들고, 그중에 y가 1일 때 3번 index가 1인 query 데이터를 만들 수가 있습니다.
어쨌든, Query를 넣고, 각 Key에 대해서 Query에 대한 유사도를 구한 후에, 다시 그 유사도를 Key 벡터들에 Weighting 한 후에 이걸 합한 걸 학습하는 것이 지금의 목표입니다.
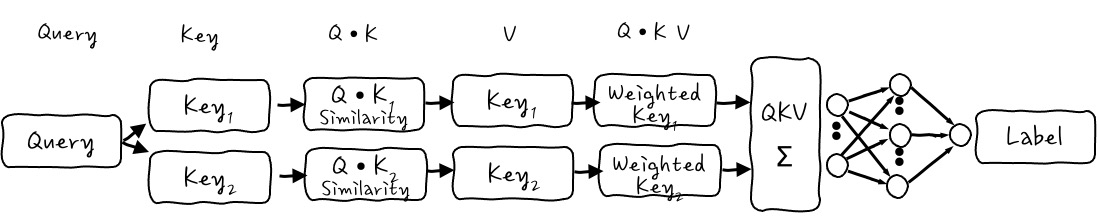
이걸 구현하면 되는데, 모형은 Keras로 매우 쉽게 구현할 수 있겠습니다.
# eager execution 모드 비활성화
tf.compat.v1.disable_eager_execution()
query = layers.Input(shape=(input_dims,), name='input')
key1 = layers.Dense(input_dims, activation='softmax', name='key1')(query)
key2 = layers.Lambda(lambda x: swap_elements(x), name='key2_raw')(query)
key2 = layers.Dense(input_dims, activation='softmax', name='key2')(key2)
queryKey1Dot = layers.multiply([query, key1], name='dot1')
queryKey2Dot = layers.multiply([query, key2], name='dot2')
queryKey1Value = layers.Lambda(lambda x: queryKey1Dot*x, name='qk1v_vector')(key1)
queryKey2Value = layers.Lambda(lambda x: queryKey2Dot*x, name='qk2v_vector')(key2)
vectorSum = layers.Add(name='qkv_sum_vector')([queryKey1Value, queryKey2Value])
y = layers.Dense(20, name='dense')(vectorSum)
y = layers.Dense(1, activation='sigmoid', name='output')(y)
model = models.Model(query, y)
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
어때요, 간단하죠? 그림을 그대로 구현한 것입니다. 이때, 미리 설명했듯이 Key₁은 query와 유사한 벡터가 되도록 나오도록 query를 softmax 해서 사용하고, Key₂는 0번 index의 데이터를 query의 3번 index 데이터와 같게 만들고 softmax를 통과시켜서 사용하려고 합니다. 이렇게 하면 Key₁, Key₂중 Key₁이 query와 내적값이 크겠죠. 이때 뾰로꾸로 사용한 layer 함수가 swap_elements입니다.
def swap_elements(x): # swap 0, 3
return tf.gather(x, indices=[3, 1, 2, 0, 4], axis=1)
자, 모형을 만들었으니, 데이터를 만들어낸 후, 훈련을 시킬 차례입니다. 두근두근
train_x, train_y = build_data(data_size, input_dims, attention_column)
history = model.fit(train_x, train_y, epochs=20, batch_size=64, validation_split=0.2, verbose=2)
>
Train on 800 samples, validate on 200 samples
Epoch 1/20
800/800 - 0s - loss: 0.9322 - accuracy: 0.6675 - val_loss: 0.7329 - val_accuracy: 0.7050
Epoch 2/20
...
Epoch 20/20
800/800 - 0s - loss: 0.1579 - accuracy: 1.0000 - val_loss: 0.1574 - val_accuracy: 0.9950
[10]:
이렇게 모형을 훈련시킬 수 있겠습니다. 헤헿
Loss를 보면,
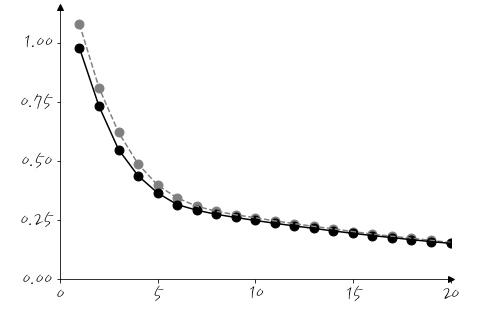
학습이 잘 되는 것처럼 보이는군요. 참고로, 검은색이 Training Loss이고, 회색이 Validation Loss입니다. 당연한 순서겠지만 테스팅 데이터를 이용해서 얼마나 잘 훈련했는지 한번 볼까요?
# Test
test_x, test_y = build_data(data_size, input_dims, attention_column)
result = model.evaluate(test_x, test_y, batch_size=64, verbose=0)
print("Training Loss:", result[0])
print("Accuracy:", result[1])
>
Training Loss: 0.21224404215812684
Accuracy: 0.984
와웃. Accuracy가 98.4%나 되는군요. 훈련이 매우 잘 되었습니다. 이 의미는 query의 3번 index의 값이 1이면 1로, 0이면 0으로 잘 예측한다는 의미입니다. 오, 그럼 결과를 봤으니까, 이제부터는 Attention 내부를 잘 한번 들여다보는 것이 좋겠습니다.
일단, Key₁과 Key₂값이 잘 들어가고 있는지 확인부터 해 보겠습니다. 대~충 layer을 다시 정리하면 다음과 같이 구성되어 있습니다.
(0) input
(1) key2_raw
(2) key1
(3) key2
(4) qk1v_vector
(5) qk2v_vector
(6) qkv_sum_vector
(7) dense
(8) output
다음은 모델 중 특정 Layer의 출력을 보는 방법입니다. 이걸 이용해 보죠. model.get_layer(Layer이름)의 이름만 바꾸면 어떤 Layer든 출력을 확인할 수 있습니다.
# key1 vector
attention_layer = model.get_layer('key1') # 이자리의 이름을 바꾸면 해당 layer의 output을 볼 수 있습니다.
func = K.function([model.input], [attention_layer.output])
output = func([test_x])[0]
print(output[:10])
attention_vector = np.mean(output, axis=0)
이런 식을 보면 Key₁ vector의 구성을 볼 수가 있겠는데, Key₁ Vector는,
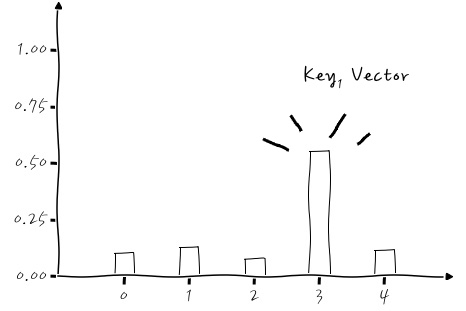
3번 자리에 데이터가 몰려있죠? 그러니까 Key₁은 query와의 내적이 클 것입니다. 같은 방법으로 Key₂ vector의 구성을 보면 (key2_raw)
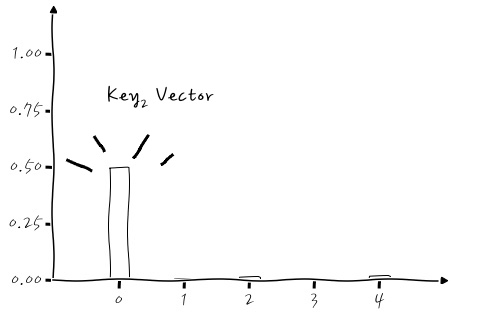
어때요, index 0에 값들이 몰려 있죠! 잘 들어가는 것 같네요. 그렇다면 마지막으로 내적 합인 qkv_sum_vector를 살펴보도록 하시죠. 이거는 미리 예상할 수 있겠죠? query•Key₁은 내적이 크고, query•Key₂는 내적이 작을 테니까, 합하면 3번 자리에 값이 크게 있을 거예요.
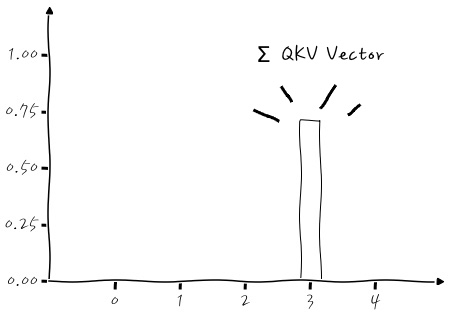
아하하. 왔습니다. 왔구요. 자, 이제 입력 값들을 봤으니까, 나머지 두 가지를 볼 수 있겠는데요, 신경망의 Weight를 보고 실제로 어떤 자리가 가장 강조될 수 있도록 학습이 되었는지 한번 볼까요?
# 신경망의 Weight를 가져옴
dense_layer = model.get_layer('dense')
weights = dense_layer.get_weights()[0]
# 각 입력에 대한 평균 Weight를 계산!
feature_weights = np.mean(np.abs(weights), axis=1)
# 입력값의 자리중 어떤 자리가 가장 영향력이 큰지 알아내자!
max_weight_index = np.argmax(feature_weights)
print(feature_weights)
> [0.17799331 0.3770768 0.18870816 0.8012823 0.31981304]
자, 어때요. 3번 자리에 대한 Weight가 가장 크죠? 이걸 그림으로 보면,
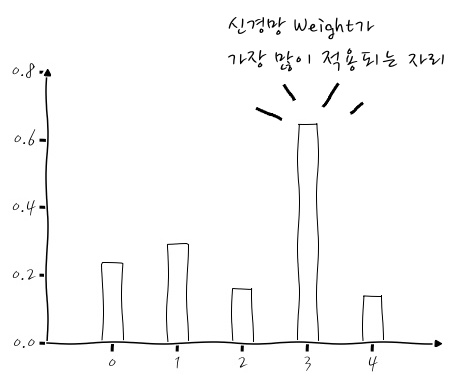
이런 식으로 3번 자리를 가장 자세하게 보도록 신경망이 학습이 되었습니다. 아핳! 그런데, 여기에서 더 신기한 걸 본다면,
Key₁과 Key₂의 Dense(Softmax)의 출력을 보잖아요? 이것도 Dense층이기 때문에 Back propagation에 참여하게 되어 학습이 되거든요.
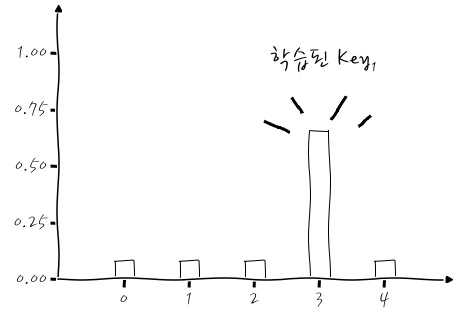
이건 Key₁이고요,
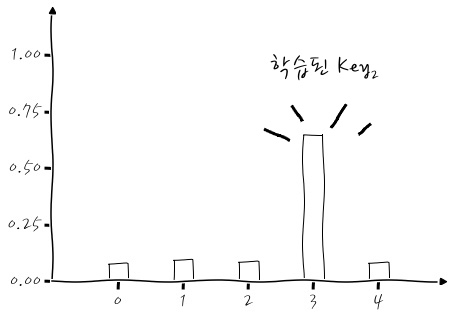
이건 Key₂에요. Key₂가 분명 index 0에 값이 몰려있어야 되는데, 3번 자리에 더 가중되도록 학습이 되었습니다. 와.
학습을 하면서 이미 Loss를 최소로 하기 위해서 Dense(Softmax) 층에서 3번 자리를 강조하면 된다는 걸 학습해 버린 겁니다. 소름. 그러니까, 이미 설명했듯이 신경망을 통해서 Key들을 회전하고 Scaling 해서 Query와의 유사도가 어느 Key와 커야 할까를 찾아내야 한다는 것을 이런 식으로 알아볼 수 있겠습니다. 대.단.하죠?

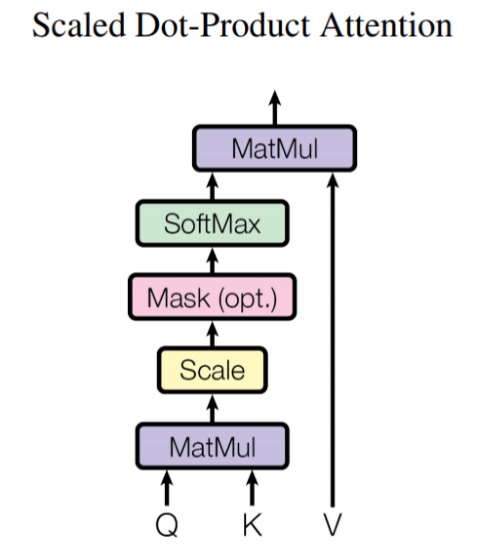
Scaled Dot-Production Attention을 표현할 때에는 이런 그림으로 표현하는 경우가 많은데, 이게 이제까지 이야기한 것과 같은 이야기입니다. MatMul이 Dot Product 한 결과이고, 노란색 Scale은 크기를 줄이는 (차원의 루트로 나눔) 일을 하는 것이고요, Softmax는 Key가 여러 개 있다면 각 Key에 대한 내적에 의한 가중치가 나오는데, 이걸 0~1 사이의 값으로 하여 가중치 합이 1이 되도록 만든 후에 해당하는 V와 Dot Product(Elementwise 곱)을 통해서 가중치 Scaling 한다는 뜻입니다. 그냥 대략적 컨셉이 이렇구나 정도 이해하시면 되겠습니다. 이제 이런 그림이 나오더라도 별거 없구만. 흡. 할 수 있지 않을까 기대해 봅니다. - Mask는 옵션입니다. 그리고 MatMul은 여기서는 Dot Product를 의미합니다. 병렬 연산을 할 때는 MatMul을 이용해서 Dot Product 연산을 합니다. -

지금은 Query가 1개일 때를 봤잖아요? 그러면, Query가 여러 개일 때는 한꺼번에 처리할 수가 있을까요? 아주 간단합니다.
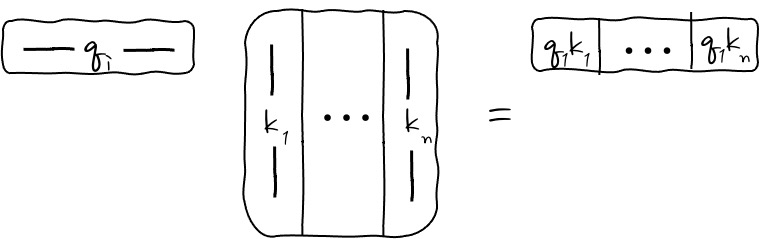
이게 하나 일 때의 내적이었잖아요? 그럼 Q를 행벡터로 주르르륵하게 되면!
이렇게 하면 병렬적으로 Attention을 계산해 낼 수 있습니다.
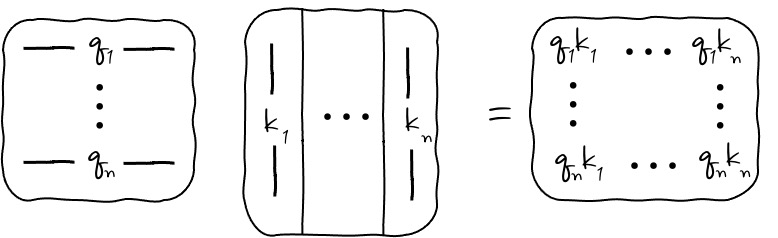
이런 식인거구요. Attention 수식으로 나타내면,
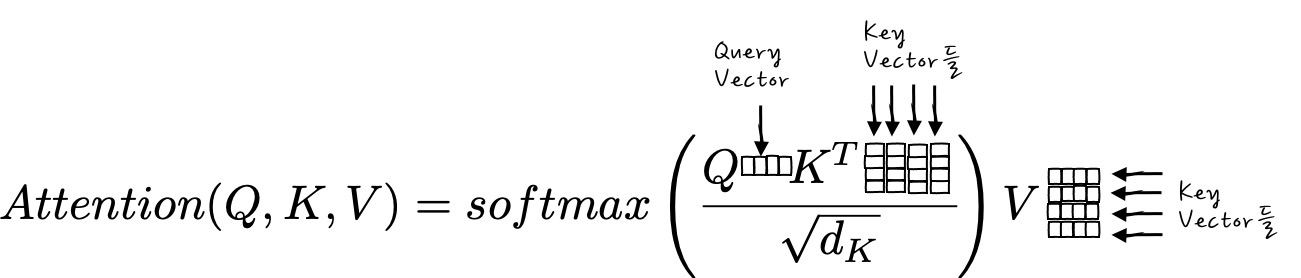
요랬는데,
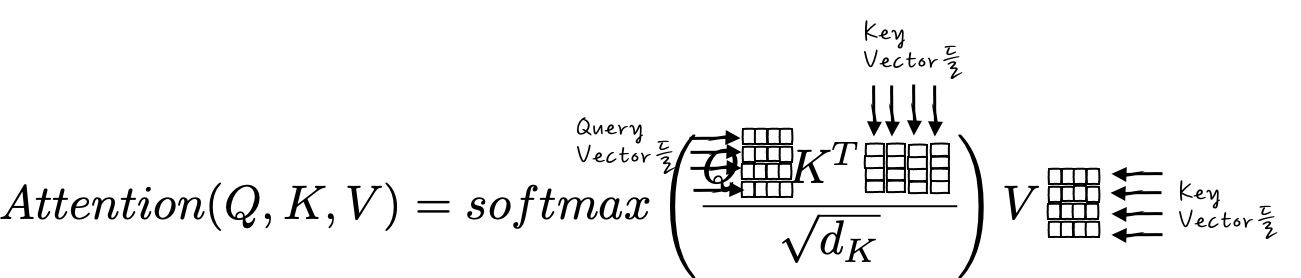
이런 식으로 바뀌는 거죠.

방금 예를 든 Query가 여러 개 있을 때, Key들을 Query들로 두고 Attention을 구하게 되면, Self Attention입니다.
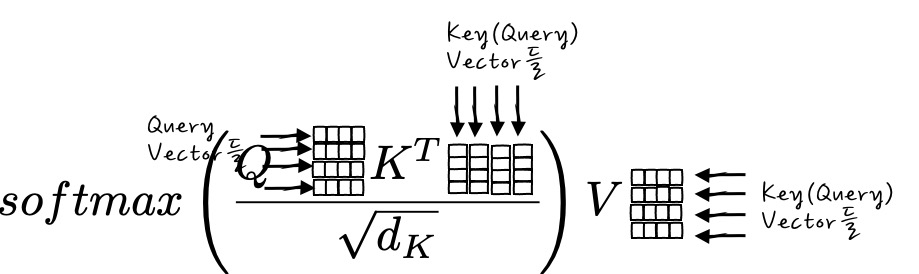
즉, Softmax() 부분만 보면,
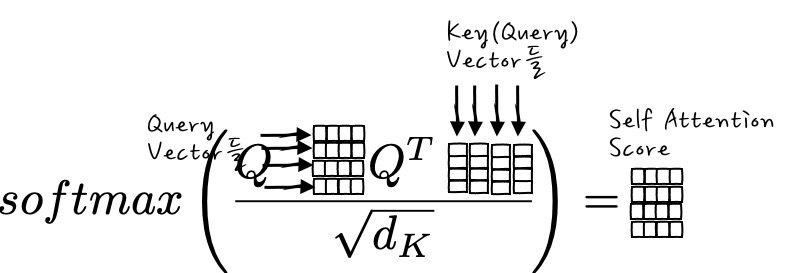
이런 식의 Correlation Matrix 같은 느낌의 Score Matrix를 구할 수가 있게 되고, 결국 Query(자기 자신)끼리의 관계 Vector합을 구하게 되는 것입니다. Self Attention의 경우에는 모두 Query만을 이리저리 가지고 하다 보니까, Query가 Query의 역할 일 때, Key의 역할 일 때, Value의 역할일 때가 달라지는 편이 좋겠죠. 그래서, $W^Q, W^K, W^V$ 라는 학습이 되는 행렬을 곱해서 학습을 시키게 됩니다. 그래서 막상 $Q = Q W^Q, K=QW^K, V=QW^V $ 형태로 정의해서 학습시킵니다.

다른 곳에서 참고할 수 있도록 늘어놓아 보면 말이죠, 이걸 RNN에 응용해 보면,
Query : t 시점의 디코더 셀에서의 은닉 상태
Keys : 모든 시점의 인코더 셀의 은닉 상태
Values : 모든 시점의 인코더 셀의 은닉 상태
이게 무슨 의미인가요? t시점의 디코더 셀의 은닉상태와 모든 시점의 인코더 셀의 은닉상태의 내적하여 이것을 Attention을 통해서 어느 인코더 셀의 은닉상태에 Attention하면 좋을지를 찾아내는 것이겠죠?
이제는 왜 이런 식으로 Key와 Value가 정해지는지 알 수 있겠죠! 캬. 좀 더 확장해 보면, Query를 Decoder의 hidden state로, Key를 Encoder의 hidden states로 하면 Seq2Seq Attention이고, Query=Key=Value라면 self Attention이고, 이 두 개를 합하면 Transformer가 됩니다. 이건 또 기회가 될 때 자세히 보도록 하시죠. 이것만 알아도 뭔가 국밥을 먹었을 때의 뜨듯하고 나른한 그런 든든함이 있는 것 같아 흐뭇합니다.
 친절한 데이터 사이언스 강좌 글 전체 목차 (정주행 링크) -
친절한 데이터 사이언스 강좌 글 전체 목차 (정주행 링크) - 

댓글