아주 이번 기회에 확실히 짚고 넘어가는 이야기.
계속 헷갈리는 용어가 있는데, 그것이 표준오차라는 말입니다. 표준편차와 한 글자만 다른데, 아무튼 다른 의미를 갖고 있으니 헷갈릴 수밖에요. 성격이 매우 급한 저로서는 처음에 그게 그거지 뭐 하고 넘어갔다가 큰 코를 다쳤는데 - 실제로는 코가 다칠 만큼 크지는 않습니다. 그때 잘-해-둘-걸 하는 생각을 하고 있습니다.
일단 표준오차도 표준편차인데, 통계량의 표준편차를 부르는 특수한 용어입니다. 표준오차는 '모수 추정값과 실제 값인 모수와의 표준적인 차이' 정도가 쉽게 이해할 수 있는 정의라 생각합니다. 표준편차라는 용어가 헷갈리지 않는다는 가정으로, 에러를 얘기하니까, 뭔가 우리가 무언가를 집계한 후 계산한 통계량의 값에 오차가 있다고 생각하면 조금은 기억하기 편할지도 모르겠습니다.
통계량 중 평균을 예를 들면, 표본을 계속 뽑아서 각 평균의 평균을 구하고, 그때의 평균들의 표준편차를 구하면 그것이 표준오차입니다. 이런 경우 중심극한정리에 의해서 표본 평균들의 표준편차인 $\cfrac{\sigma}{\sqrt{n}}$ 가 표준오차가 됩니다. 그러니까 우리가 구하는 통계량의 표준편차가 표준오차입니다. 보통 영어로는 SE(Standard Error)라고 부르고요. 즉, $\cfrac{\sigma}{\sqrt{n}}$, 표본의 크기가 클수록 그 분산이 0에 가까워져서 표본평균은 모평균 근처에 밀집합니다. - 이 경우, 엄밀히 말해 σ는 모수(상수)이기 때문에 표준오차라고 부르면 안된다고 굳이 구분하는 경우도 있는데, s로 바꾸면 명확하게 표준오차가 되니 굳이 구분하기 보다는 표준오차가 어떤 것인지만 잘 알면 좋겠습니다. -
그러면 표본의 표준편차의 표준편차도 구할 수 있을텐데, 이것도 표준오차라고 부를 수 있습니다. - 쓸 데가 없긴 하지만요 - 참고로 회귀분석에서 회귀계수의 표준편차도 표준오차입니다. 통계량의 표준편차니까요.
또 한번 반복해서 얘기하는데, 표준오차는 통계량의 표준편차를 표준오차라는 것을 머릿속에 잘 새겨 넣고, 통계량의 표준편차를 보면 삐삐 하고 자동으로 신호를 보내서 표준오차. 표준오차 다시 한번 말한다. 표준오차. 이런 식으로 곧바로 변환해야 합니다.
이제, 또 헷갈리는 용어들에 대해서 이야기해 보면, 표본오차, 오차한계, 최대허용오차, 오차범위, 표집오차 등의 용어가 있는데 이건 또 무엇인가 하면, 사실은 표본오차 = 오차한계 = 최대허용오차 = 오차범위 = 표집오차 모두 같은 말입니다. 그냥 편한 대로 부르는 꼴입니다.
정의부터 이야기 하자면, 표본오차, 오차한계, 최대허용오차, 오차범위, 표집오차는 임계값(Critical Value)에 표준오차를 곱한 값입니다.
그러니까, 처음 들어보는 뭔가 표준이라는 말이 붙어 있지 않은 오차라는 게 있다면 표준오차에 임계값을 곱한 것이구나 정도로 합리적인 유추를 하면 편리할 것이라 생각합니다. 사실, 표준오차는 한가지 값으로 정해지지만, 나머지 오차들은 모두 신뢰도에 따라 다르게 정해집니다. 왜냐하면 임계값$z_{critical}$을 곱하게 되니까요.
중심극한정리에서의 신뢰구간을 따질 때를 예로 들면, 평균의 표준편차는 표준오차라 하고, 신뢰구간을 위한 임계값이 곱해진 전체가 표본오차라고 부르면 됩니다.
그러니까 95% 신뢰도의 평균의 표본오차의 경우에는 표준오차를 곱해서 아래와 같이 계산하면 됩니다.
즉, $z_{2.5\%}\cfrac{\sigma}{\sqrt{n}}$ 입니다.
여기에서 $z_{2.5\%}$가 임계값(Critical Value)입니다. 이 값이 우리가 95% 신뢰도에 많이 사용하는 1.96이죠.

여기에서 모분산 $\sigma$가 알려져 있지 않은 경우 표본표준편차를 이용하고, t분포를 이용해서 , $z_{2.5\%}$ 대신에 $t_{2.5\%}$를 사용하기도 합니다. 대부분의 경우 이것이 현실적이겠죠.
결국 $t_{2.5\%}\cfrac{s}{\sqrt{n}}$ 이 표본오차, 오차한계, 최대허용오차, 오차범위, 표집오차등 이라고 보면 되겠습니다.

특히 오차범위라는 용어는 보통 언론사에서 표분비율을 기사화할 때 이런 용어를 즐겨 쓰는데, 일부 언론사 기사의 예를 한번 보면,
‘성인 남녀 1000명을 대상으로 한 여론조사에서 응답률 15%, 대통령의 국정운영에 대한 지지율 20%, 오차범위는 ±3%p’ 여기에서 ±3%p가 $ \pm z_{2.5\%}\times$ 표준오차를 계산한 것입니다.
이런 경우의 오차 범위를 조금 산수를 통해서 본다면, 이 조사는 독립인 성공확률 p인 Binomial Trial을 n번 한 것과 같으니까, 표본 비율에 대한 표준편차를 표준오차라고 하고, 이것은 $\hat{p}$는 $N\left(p, {\cfrac{n\hat{p}(1-\hat{p})}{n^2}}\right) = N\left(p, \cfrac{\hat{p}(1-\hat{p})}{n}\right)$을 따르니까, 당연히 $ \sqrt{\cfrac{\hat{p}(1-\hat{p}) }{n}}$가 표준오차가 되고, 이것을 신뢰도의 임계값을 곱하게 되면, 결국 오차범위는
$$ e = \pm z_{2.5\%} \sqrt{\cfrac{\hat{p}(1-\hat{p})}{n}}$$
가 되고, 만일 95% 신뢰수준이라면
$$ e = \pm 1.96 \sqrt{\cfrac{\hat{p}(1-\hat{p})}{n}}$$
가 됩니다. 후후. 여기에 p=0.5, n=1000을 넣고 계산해 보면 약 3.1%p가 나옵니다. 어머나! - p=0.5를 넣는 이유는 조금 뒤에 다뤄질 테니, 조금만 기다려주세요-
간단하죠. 그런데?! 우리가 늘 보는 여론조사는 이렇게 간단하게 찬성/반대만 있지는 않지 않나요? 보통은 다음의 기사와 같이 두 후보의 지지율 차이를 기사화하는 경우가 많죠.
‘성인 남녀 1000명을 대상으로 한 여론조사에서 응답률 15%, 갑 후보 지지율 40%, 을 후보 지지율 37%, 신뢰수준 95%, 오차범위는 ±3%p’
허허 그렇군요. 이 기사를 잘 해석해 보면, 모집단 중 1000명을 뽑아 조사를 실시했을 때 갑 후보 지지율 37~43%, 을 후보 지지율 34~40%이고, 신뢰수준은 95%라는 얘기입니다. 그렇다면 정말 지지율 차이가 있다는 얘기일까요? 이것을 오차범위를 이용해서 해석할 수 있겠습니다.
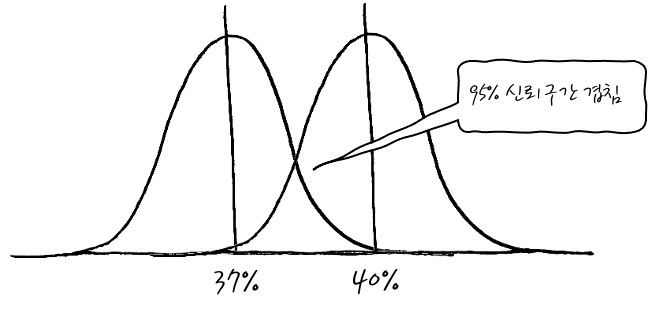
지지율을 잘 보면 잘 보면 두 후보의 95% 신뢰구간이 37%~40% 사이에 서로 겹칩니다. 그러니까, 실은 두 후보의 지지도가 뒤집힐 수 있는 구간이 있다고 보면 되겠습니다. 호오. 이 의미는 차이가 날 수도 있고, 안날 수도 있다는 의미입니다. - 조금 자세하게 이야기 해 보자면, 지지도 신뢰구간이 겹치면 차이가 날 수도 안날 수도 있습니다. 아무도 모른다는 의미일 수도 있고요, 하지만 신뢰구간이 겹치지 않으면 차이가 난다고 볼 수 있겠습니다. -
그러면, 그다음에 이런 기사가 나왔다면 어떨까요?
‘성인 남녀 1000명을 대상으로 한 여론조사에서 응답률 15%, 갑 후보 지지율 43%, 을 후보 지지율 33%, 신뢰수준 95%, 오차범위는 ±3%p’
흠, 갑 후보는 95% 신뢰도에 의한 신뢰구간은 40~46%, 을 후보는 30~36%가 되겠군요.

그림을 보면, 두 후보의 95% 신뢰구간이 겹치지 않습니다. 이런 경우라면 확실하게 어느 후보의 지지율이 더 높은지 확실하게 알 수 있겠습니다. 아! 그런 의미군요.
여기까지는 흔히들 얘기하는 언론의 통계 분석 방식인데, 조금 이상하지 않나요? 95% 신뢰도에 의한 오차범위를 다시 써보면 아래와 같습니다.
$$ e = \pm 1.96 \sqrt{\cfrac{\hat{p}(1-\hat{p})}{n}}$$
분명히 찬/반 2개만 있을 때는 확실하게 맞는 이야기이긴 합니다만, 각각의 후보의 비율이 다르니까, 오차범위가 3.1%p 하나로 나오는 것이 이상하지 않나요? 각 1번 2번 후보에 따라 표본비율이 $\hat{p_1}, \hat{p_2}$로 다를 텐데요.
예를 들어, 첫 번째 예에서는 ‘성인 남녀 1000명을 대상으로 한 여론조사에서 응답률 15%, 갑 후보 지지율 40%, 을 후보 지지율 37%, 신뢰수준 95%, 오차범위는 ±3%p’
이니까, 갑 후보의 오차범위는 3.03%p, 을 후보의 오차범위는 2.99%p이어야 할 것 같은데 3%p 한 가지 값으로 따집니다.
두 번째 예에서도, ‘성인 남녀 1000명을 대상으로 한 여론조사에서 응답률 15%, 갑 후보 지지율 43%, 을 후보 지지율 33%, 신뢰수준 95%, 오차범위는 ±3%p’ 이니까, 갑은 3.06%p, 을은 2.91%p로 각각 오차범위를 따져야 할 것 같은데 또 3.0%p 한 개의 오차범위로 따지고 있습니다. 이게 어떻게 된 일일까요?
실제로 정확하게 "다항" 표본비율끼리의 차이에 대한 95% 신뢰구간은
$$p_i - p_j = \hat{p_i} - \hat{p_j} \pm 1.96 \sqrt{\frac{\hat{p_i}+\hat{p_j} - (\hat{p_i}-\hat{p_j})^2}{n}}$$ 이 정확한 표현입니다. 일단 자세한 내용은 아래의 논문을 참고해 주세요.
그러니까 두 비율의 차이가
$$ 1.96 \sqrt{\frac{\hat{p_i}+\hat{p_j} - (\hat{p_i}-\hat{p_j})^2}{n}} $$
이상 나야 두 비율 간의 차이가 있다고 말할 수 있다는 것입니다.라는 이야기는 그런 것이 있었지 않나? 정도로만 하고 크게 실례가 되지 않는다면 그냥 넘어가도 좋지 않을까? 하는 적당주의라는 편리함을 고개를 드는데, 적당주의를 잘 이용하는 것도 그렇지 않아도 짧은 인생을 잘 살아가는 방법 중 하나가 아닐까 합니다.
두 번째 예라면, 이런 정확한 비율 차이를 이용해서 다시 계산한 결과가 5.37%p입니다. 두 후보의 지지율 차이가 10%p니까, 확실하게 차이가 난다고 말할 수 있겠군요. 이렇게 따졌으면 좋겠는데, 한국의 언론은 이렇게 통계 결과를 발표하지 않고, 다른 방식으로 오차범위를 산정하고 있습니다.
어, 그렇군요. 어떻게 산정하고 있는 것일까요? 한국의 통계는 그냥 p에 0.5를 넣어서 오차범위를 대략 산정하고 있습니다.
$$\left. e = \pm 1.96 \sqrt{\cfrac{\hat{p}(1-\hat{p})}{n}} \right\rvert_{\substack{\hat{p}=0.5\\n=1000}} = \pm 1.96 \sqrt{\cfrac{0.5\times0.5}{1000}} = \pm 3.1\%p$$
이게 무슨 의미냐 하면 어떤 비율을 볼 때, 하나의 모집단에서 얻은 표본 비율로 모비율을 추정할 때 발생하는 오차범위가 가장 불확실성이 클 때를 따졌을 뿐이라는 점입니다. 최악의 경우를 상정해서 (0.5의 비율이면 불확실성이 가장 커서 - 유식한 말로는 Entropy가 가장 커서 -), 이렇게 대략 계산하자는 뭐 그런 것입니다. 그러다 보니까, 언론의 통계는 표본 수만 정해지면 각각의 비율에 대한 오차범위가 자동적으로 구해집니다. - 이런 점 때문에 두 비율 비교 시에 발생할 수 있는 정확한 오차범위는 아닌 점을 알고 있으면 의문이 좀 덜 하게 됩니다.
그러니까, 오히려 언론의 기사는 오차범위를 알면 표본수를 거꾸로 알게 되는 좀 이상한 통계입니다.
앞서 보았던 표준오차를 n으로 다시 정리하고 (p=0.5를 넣고) $n = \cfrac{1.96^2 \cdot p(1-p)^2}{e^2} = \cfrac{1.96^2 \cdot 0.5^2}{e^2}$ 이고요,
방금 본 기사가 3.1%p 오차범위(e)니까, n = 1000명이라는 그런 심플함. 그러니까 어, 1000명 표본으로 했나 보군. 뭐 그런 걸 알게 되는 거꾸로 셈법인 셈입니다.

조사대상이 1000명일 때 응답률이 15%라는 건 1000명 중 15%인 150명이 응답을 했다는 뜻이 아니라, 1000명의 응답을 받기 위해서 6667명에게 조사를 해서 그중 15%인 1000명에게 응답을 받았다는 뜻입니다.

그러면 선거조사에서 두 명의 후보에 대해서 다음의 두 경우를 보면 겹치는 경우와 겹치지 않는 경우가 있는데 겹치는 경우에는 오차범위 내 접전, 그렇지 않은 경우에는 우세라는 표현을 쓰고 있습니다. 그러니까 오차범위가 겹치는 첫 번째 경우에는 접전, 오차범위가 겹치지 않는 두 번째의 경우에는 우세라고 표현할 수 있겠군요.

다항표본분포에 대한 오차범위는 Scott, A.J and Seber, A.F (1983), Difference of Proportions From the Same Survey, The American Statistician, Vol. 37, No. 4, 319-320을 참조하면 좋겠습니다.

그러니까 두 비율의 차이가 $$ 1.96 \sqrt{\frac{\hat{p_i}+\hat{p_j} - (\hat{p_i}-\hat{p_j})^2}{n}} \cdots (*)$$
이상 나야 두 비율 간의 차이가 있다고 말할 수 있다는 것입니다.라는 의미가 조금 어려울 수 있는데, 이 의미는 두 표본비율이 같다는 Null Hypothesis와 다르다의 Alternative Hypothesis를 설정했다면, *값 이상 차이가 나야 95% 신뢰도로 검정을 하게 되었을 때 p_value가 5%보다 작게 되니까, Null Hypothesis를 기각할 수 있다는 의미입니다. 검정을 아직 살펴보지 않았는데, 이런 이야기를 꺼내게 되어 미안합니다.

이해를 돕기 위하여 한 가지만 더 예를 든다면, 한 여론조사기관에서 2~30대 연령의 남녀 600명을 대상으로 직장에서 사랑에 빠진 경험이 있는지를 조사한 결과 전체의 57.2%가 그래 본 적이 있다고 답을 하였다고 했을 때, 실제로 50% 이상이 직장에서 사랑에 빠진다고 발표해도 괜찮은지?에 대한 문제를 생각해 본다면,
95% 신뢰도에 의한 표본오차는 $1.96 \times \sqrt{\cfrac{0.572(1-0.572)}{600}} = 0.04$입니다. 이런 경우라면, 4%p가 표본오차니까, 0.572-0.04 ~ 0.572+0.04이므로, 0.532~0.612가 되므로, 실제로 50%가 넘는다고 발표를 해도 됩니다. 그렇지만, 100명을 대상으로 조사한다면, 표본오차는 9.7%p가 되므로, 0.475~0.669가 되어 그렇다고 발표하기가 어렵게 된다는 그런 이야기도 덧붙입니다.
 친절한 데이터 사이언스 강좌 글 전체 목차 (정주행 링크) -
친절한 데이터 사이언스 강좌 글 전체 목차 (정주행 링크) - 

댓글