최대우도추정법(MLE)을 산수를 곁들여 즐기는 향유

우도에 대한 카오스를 경험할 때 이전에 약속한 대로 최대우도추정 MLE (Maximum Likelihood Estimation)을 한번 살펴볼 생각입니다. - 아니 최대우도추정이라는 말은 너무 어려운 거 아닌가요? -

MLE최대우도추정은 관측한 데이터를 통해 Parameter모수를 추정하는 방법입니다. 모수를 추정할 때, 이제까지는 신뢰구간을 이용해서 추정했지만 이번에는 한 개의 숫자로 추정을 해 볼까 합니다.  -이번 이야기도 Likelihood, 우도, 가능도를 마구 섞어 쓸 예정이니, 무엇을 보더라도 같은 것으로 인식하는 훈련으로 생각해 주세요. -

일단, MLE의 특징은 가장 적절한 분포를 먼저 가정하고, 그 가정된 분포에 대한 가장 적절한 모수θ를 찾아낸다는 것인데, 그 모수θ를 찾아내기 위한 근거가 무엇인가 하면 Likelihood를 이용하는 것입니다. $\mathcal{L}(θ|x)=P(x|θ)$를 벌써 잊지는 않으셨겠지요. Likelihood를 보면 어떤 데이터를 관측했을 때, θ에 대한 그럴듯함에 대한 강도이니까, 이것을 이용하면 되겠다! 유레카 뭐 그런 것인데, 그러면 당연히 θ에 대한 Likelihood의 최댓값을 찾아내면 그때의 θ가 가장 데이터를 잘 설명하겠군. 음음. 그렇군 하는 이야기인데, 이렇게 접근하면 딱 이야기가 그럴 듯 해 집니다.. 그러면 최댓값은 어떻게 구하는가 하면 당연히 미분해서 그 값이 0인 것을 찾아내면 되겠군요. 즉,  $(\frac{\partial{\mathcal{L}}}{\partial{\theta}}=0)$. 물론 위로 볼록한 우도 함수이어야겠지요. 우도 함수가 변곡점 없이 무한정 발산하는 경우는 없으니까 걱정은 없습니다. 미분의 위대함이겠습니다. 

그러면, 이 이야기를 앞서 이야기 했던 10번 Trial에 7번 Success했던 예를 들어 산수적으로 접근해 보겠습니다. 

조금 더 흥미롭게 각색하자면, 주머니 안에, 카드가 100개가 있는데, 검은 카드와 흰색 카드가 있습니다. 10번을 뽑아 보았더니, 검은 카드가 7번 흰색 카드가 3번 나왔습니다. 그러면 검은 구슬은 전체 구슬 중 몇 개가 있을지 추정해 봅시다. 이걸 MLE로 풀어보자는 얘기입니다. 여기에서 모수θ는 p이겠군요.

자, 그러니까 이것은 Binomial로 확률 분포를 모델링 할 수 있다는데 이의가 없을 것입니다. 

A : 검은 카드 Event, n = 10, p = 검은카드 확률이라고 했을 때 P(A)는

$$P(A) = \dbinom{n}{k} \cdot p^kq^{n-k}  = C \cdot p^kq^{N-k}\Biggr\rvert_{\substack{k=7\\n=10}} = C \cdot p^7 (1-p)^3$$

입니다. 여기에서 우리가 추정하는 모수는 p 이고, C는 Constant입니다.  

결국, 

$$ \hat{p} = \underset{p}{argmax}  (C \cdot p^7 (1-p)^3)$$
우리가 추정하는 모수 $\hat{p}$는 위의 식을 만족하는 p를 구하면 됩니다. 

최대값을 찾을 때는 미분을 하는 것이 정석인데요, 미분을 할 때 특히 power형태의 수식을 미분해야 할 때는 log를 씌우면 모든 power행태가 곱셈으로 바뀌고, 곱셈이 더하기로 바뀌니까 매우 편리한 형태가 된다는 점을 기억하면 언제나 요긴하게 사용할 수 있습니다. 특히 log는 $x_1,x_2$에 대해서 값이 증가할 때, log를 씌운 값도 같이 증가하게 되므로, 최댓값을 찾을 때는 똑같은 결과를 갖습니다. 

Linear function에 log를 취해보면 monotonically increasing 합니다. 이것의 의미가 원래 함수의 최대값을 갖는 점과 log를 취한 함수의 최댓값을 갖는 점은 같다는 뜻입니다. 자연로그 ln으로 취했을 때도 같다는 점도 알고 있으면 Gaussian을 미분할 때 편리하겠습니다. 조금 의심이 드니까, 실제로 그런지 이전에 보았던 Binomial Likelihood를 log를 씌워서 보면 

정말 그렇지요? 미분을 했을 때, 최대값이 log를 씌운 것이나, 아닌 것이나 같을 것입니다. 자 그럼 $\hat{p}$를 구해보면, - 여기에서 p가 모자를 쓴 이유는 추정 값이라는 뜻입니다. -

$ \begin{aligned}\hat{p} &= \underset{p}{argmax} (C \cdot p^7 (1-p)^3) \\ &→ \underset{p}{argmax} (log(C \cdot p^7 (1-p)^3)) =  \underset{p}{argmax} (log(C) + 7\cdot log(p) + 3\cdot log(1-p) )
\end{aligned} $

여기에서 p에 대해서 미분을 한 것을 계산하면,
$\cfrac{d (log(C) + 7\cdot log(p) + 3\cdot log(1-p))}{dp}=0$ 이니까,
$ \cfrac{7}{p} - \cfrac{3}{1-p} = 0$를 풀면 됩니다. 완전 쉬워졌네요. 후후.

결국 p = 7/10 가 됩니다. 오 우리가 처음 10번 중에 7번 검은 카드를 봤는데, 그것이 그대로 전체 비율의 추정 값이 되는군요. 100개 중 70개가 검은 카드일 듯? 하고 추정하는 것이 결론입니다. 이것이 가장 간단한 MLE 문제를 산수를 이용해서 하는 풀이인데, 너무 쉬운 것 아닌가. 하는 의문이 있을 수 있으니, 한 가지 더 해보겠습니다.

아참, 그러고보니, MLE를 할 때, 굉장히 중요한 것이 있습니다. 모든 Observation은 i.i.d라는 점이고, i.i.d이기 때문에 각각의 Observation에 대해서 곱하기 형태의 joint probability를 쓸 수 있다는 점입니다. 먼저 살펴본 예의 카드 뽑기도 각각의 표본을 뽑을 때마다 i.i.d인 Binomial Trial case였습니다. 

예를 들어, Gaussian Distribution에서 모수인 μ를 MLE로 추정해 보시죠. Gaussian Distribution의 pdf는 다음과 같습니다. 지난 번에도 잠깐 이것을 이야기할 기회가 있었는데, Gaussian Distribution의 pdf를 외우고 있으면 그렇게 간지가 날 수 없습니다.라고 믿고 있습니다. 

$$
P(x ; \mu, \sigma)=\frac{1}{\sqrt{2 \pi \sigma ^2}} e^ \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right)
$$

자, 이런 분포를 갖는 데이터에서 9, 10, 11을 Observe했습니다. 이런 경우에 어떤 Gaussian 분포가 이 데이터를 제일 잘 설명할까요? μ에 대한 함수인 Likelihood! 다시 등장

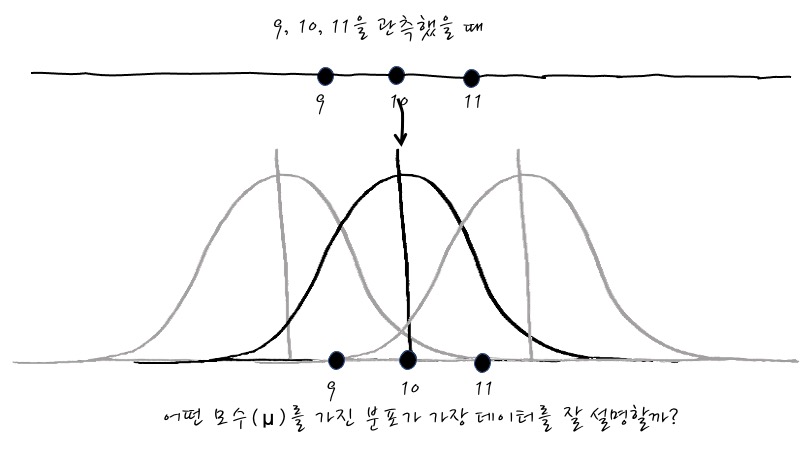
이럴 때, MLE로 모수를 추정하기 위해 3개 Observation에 대한 joint probability를 표현하면, (e의 power를 보기 좋게 exp로 표시해 보겠습니다)

$$
\begin{aligned}
P(9,10,11 ; \mu, \sigma) &=\frac{1}{ \sqrt{2 \pi \sigma^2}} \exp \left(-\frac{(9-\mu)^{2}}{2 \sigma^{2}}\right) \\& \times \frac{1}{ \sqrt{2 \pi \sigma^2}} \exp \left(-\frac{(10-\mu)^{2}}{2 \sigma^{2}}\right) \\& \times \frac{1}{ \sqrt{2 \pi \sigma^2}} \exp \left(-\frac{(11-\mu)^{2}}{2 \sigma^{2}}\right)
\end{aligned}
$$

로 표현할 수 있겠습니다. 오. i.i.d니까 곱하기 형태로 관리할 수 있어서 좀 편리하네요. 

그러면 방금 사용한 log를 씌우는 팁을 다시 사용해서 log를 씌워보겠습니다. 이번에는 e의 power니까 자연로그 ln을 씌우면 e가 모두 날아가겠군요. 

$$
\begin{aligned}
\ln (P(x ; \mu, \sigma))&=\ln \left(\frac{1}{\sqrt{2 \pi \sigma ^2}}\right)-\frac{(9-\mu)^{2}}{2 \sigma^{2}}\\&+\ln \left(\frac{1}{ \sqrt{2 \pi\sigma^2}}\right)-\frac{(10-\mu)^{2}}{2 \sigma^{2}} \\
&+\ln \left(\frac{1}{\sqrt{2 \pi\sigma ^2}}\right)-\frac{(11-\mu)^{2}}{2 \sigma^{2}}
\end{aligned}
$$

이 되겠습니다. 오흥. 조금 쉬워졌네요. 

$$
\begin{aligned}
\ln (P(x ; \mu, \sigma))= 3\cdot \ln \left(\frac{1}{\sqrt{2 \pi \sigma ^2}}\right)-\frac{1}{2 \sigma^{2}}\left[(9-\mu)^{2}+(10-\mu)^{2}+(11-\mu)^{2}\right]
\end{aligned}
$$

자, 이것을 $\mu$에 대해서 미분을 해서 Max값을 찾으면, 

$$
\frac{\partial \ln (P(x ; \mu, \sigma))}{\partial \mu}=\frac{1}{\sigma^{2}}[9+10+11-3 \mu] = 0
$$   

$$ \mu = \cfrac{9+10+11}{3} = 10 $$ 이 되겠습니다. 오, MLE로 추정한 μ를 찾았습니다. 9, 10, 11을 평균 낸 것과 결과가 같군요?

i.i.d가 갑자기 튀어나왔는데, 이것은 Independent and Identical Distribution의 약자인데, 각 데이터를 뽑을 때, 같은 분포에서 서로 독립인 경우를 말하는데요, 각각의 사건은 같은 분포에서 나오고, 각각의 사건은 서로 영향을 미치지 않는다는 뜻입니다.