내 주변에는 어찌된 일인지 중심극한정리를 다음과 같이 이해하고 있는 사람이 많이 있습니다.
어떤 분포이던지, 샘플을 아주 많이 뽑으면 확률분포가 가우시안으로 수렴한다.고 중심극한정리를 설명하고 마는데, 그것 참 편리한 생각이 아닐 수 없습니다. 그렇다고 함은 이 세상의 모든 사건은 가우시안을 따라야 되는데, 잠깐만 생각해도 어, 그런가? 하는 의구심이 고개를 진짜? 하고 드는 건 저뿐인가요?
사실, 중심극한정리는 극한이라는 말 때문에 그런 오해를 뒤집어쓰고 다닌다고 해도 과언이 아닙니다. 세계 곳곳에 이런 사람이 수없이 산재한다고 생각하니 도대체 통계용어는 왜 이렇게 어렵게 지어서 문제를 만드는 건지 참으로 알다가도 모를 일이네요.
제 생각에는 아마도 Binomial(이항) 분포의 n을 많이 키우면 Gaussian(정규)분포가 된다는 것 때문에 이런 오해가 생기는 것이 아닌가 생각도 듭니다.
다시 한번 중심극한정리를 정확하게 정리하면
샘플링을 해서 그 샘플에 대한 평균을 (무한히) 계속 내 보면 그 "평균의 분포"는 "실제 분포와 상관없이" 가우시안 분포이다.
그것이 우리가 흔히 말하는 중심극한정리의 정체입니다.
정리해서 말하면,
n 이 커지면 $ \bar{X}$ 는 평균이 μ이고 분산이 $\frac{\sigma^2}{n}$인 정규분포, 즉 $N(\mu,\frac{\sigma^2}{n})$ 을 따른다고 할 수 있습니다.
이게 중요한 이유는 평균의 분포가 가우시안이니까, 어떠한 분포더라도 평균만은 어느 정도 우리가 잘 예측할 수 있다는 의미입니다. 그러니까, 중심극한정리에서 극한이라는 말에만 집중할 것이 아니라, 평균에 관한 이라는 숨겨진 말을 꼭 되새길 필요가 있다는 점을 다시 한번 생각할 따름이죠. 틀림없이.
실제로 중심극한 정리에 의해 평균의 분포가 정규분포에 가까워 지는 지 확인하는 방법으로는, 모집단(분석의 대상이 되는 집단)에서 n개씩의 샘플을 N회 복원추출한다고 할 때 n이 약 30 이상의 너무 적지 않은 개수이고 시행횟수 N이 많아질수록 매 회 n개씩을 뽑아 만든 평균들을 모아보면, 정규분포를 따르는 것을 눈으로 확인할 수 있습니다. N은 무한히 할 수 없으니까 100~150번 정도라고 할까요. 이 이야기에 대한 어떤 독자의 문제 제기가 있어, 자세한 설명은 마지막에 더 자세하게 정말일까?라는 자세로 원래 취지와 다르게 긴 이야기를 덧붙였습니다.
좀 어려우니까 예를 들어 정리하면, 표본평균분포란, 내가 수집한 표본을 의미하는 것이 아니라 "모집단에서 표본크기가 n인 표본(n=30개)을 여러 번 반복해서 추출(N=200번)했을 때 (즉,$ X_1(n=30),\, X_2(n=30),\, X_3(n=30),\, \cdots X_{200}(n=30)$, 각각의 표본 평균들($Mean(X_1(n=30)),\, Mean(X_2(n=30)),\, Mean(X_3(n=30)),\, \cdots Mean(X_{200}(n=30))$)이 이루는 분포"를 말합니다. 그 표본의 크기가 커질 수록 (보통 n=30 이상), 표본 평균들이 이루는 분포가 모집단의 평균 μ, 표준편차 $\frac{\sigma}{\sqrt{n}}$인 정규분포에 가까워진다는 정리입니다.
그러니까, 표본 평균 분포의 표준편차 - 사실 표준오차 라고 부르는데, 그것은 다음에 더 얘기하기로 해요 -를 구하기 위해서 여러번 표본을 추출한 후 그 평균들을 이용해서 구해야 하는데, 충분한 표본크기(n개의 샘플)만 있다면 그렇게까지 하지 않아도 된다는 의미이기도 합니다. 오.
그러니까, 중심극한정리의 극한은 표본을 한번에 많이 뽑기만 하면 확률 분포가 가우시안의 형태를 띈다는 말은 사실이 아니에요. 오해를 풀어요 우리.
중심 극한 정리를 여러가지 버전으로 정리하면요.
• 표본 평균(sample mean)들이 이루는 분포는 복원추출 횟수가 경우 모집단의 원래 분포와 상관없이 가우시안 분포를 따름.
• 동일한 확률 분포를 따르고 서로 독립인 N 개의 확률 변수의 관찰값의 평균값은 N 이 충분히 크다면 가우시안 분포를 따름.
• N 개의 확률 변수가 어떤 확률 분포를 따르든지 상관없이 N 이 충분히 크다면 그 합은 가우시안 분포를 따릅니다.(Generalized CLT theorem)
오해를 하지 말아야 할 것은 방금 말했듯이 표본의 값을 확률변수로 하는 것이 아니라, 표본의 평균값이나, 합을 확률 변수로 놓으면 그렇다는 사실이에요.
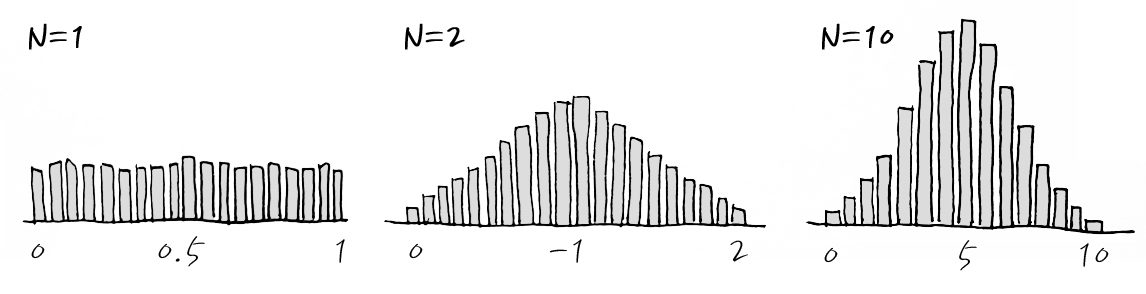
서로 분포가 같고 독립 사건의 경우에도 많이 시도해서 관측치의 합을 내거나, 평균을 내면 가우시안으로 근사할 수 있게 되는데, 심지어 Uniform 분포도 아래와 같이 근사 되는 것을 알고 있으면 조금 더 마음이 편해집니다.
표본의 평균의 경우
표본의 합의 경우
자세히 보면 아래 x축의 범위가 다릅니다. 왜냐하면, 합이니까요.
이걸 -1~1의 Uniform Distribution으로 바꾸고 pdf로 다시 그려보면 이런 식입니다. 조금 더 pdf스러워졌죠. 마지막은 n이 3이상일 때 정도로 이해해 주세요.
Central Limit Theorem의 유래에 대해서 두 가지 설이 있는데, 첫 번째는 George Polya가 1920년대에 발표한 논문에서 가우시안 분포가 확률에서 'central role'을 한다고 썼던 것에서부터 유래한다고 합니다. 게다가 독일 버전(zentraler Grenzwertsatz)으로는 central은 theorem을 꾸미는 말이지 limit을 꾸미는 말이 아니라고 하니, 정확히 표현하면 '아주 중요한 많이 시행했을 때 정리' 정도로 이해하는 것이 그렇게 나쁜 이해는 아닌 것 같습니다. 하지만, 두 번째가 더 의미있는 유래라고 생각하는데, Central은 아~주 예전에 평균을 의미했다고 합니다. 그러니까 "평균에 대한 아주~ 많은 표본에서의 정리" 정도라고 해석하면 더 Make sense한 것 같긴 합니다. 헤헷.
그러면 도대체 중심극한정리를 어떻게 이용할 수 있는가? 하면 뒤에서 분명히 활용과 사례를 들거니까, 그때 한번 유심히 살펴봐요. 중심극한정리가 왜 통계에서 중심이 되는 정리인지 그 위력을 알게 될 것이라 생각합니다.
세상에는 생각보다 많은 것들이 가우시안을 따르지 않는다는 것이 사실입니다. 중심극한정리에 의해서 확률변수의 합은 가우시안을 따른다는 것만이 사실인데, 알려지지 않은 분포의 확률변수를 가우시안으로 가정하기 때문에 결론에 대한 문제가 발생하는 경우가 많습니다. 보통 조금 많은 표본을 뽑았는데, 이게 가우시안을 보이지 않는다고 해서, 중심극한정리에 대한 오해로 어 표본 수가 너무 작은가? 하고 더 많이 뽑아봐야 표본의 크기가 커질수록 원래의 비대칭성 모양이 더 강화되니, 그에 맞는 확률 분포가 있는 것은 아닐까 의심하는 것도 타당한 접근이고, 표본의 크기가 커진다는 것은 어떤 모집단의 분포를 추정하는데 더 믿을 만 하다는 점을 잊지 말아 주세요.
마지막 부분에 문제제기가 있어서 역시나 중심극한정리는 어디서든 늘 말썽이구나 하는 생각이 또 들었습니다. 다시 한번 무엇을 잘못 설명한 것인지 곰곰이 생각하고, 요모조모 따져보았습니다. 비교적 쉽게 설명할 수 있을 것이라 생각했는데, 긴 이야기가 될 수 있을 것 같습니다만, 꽤 흥미로운 이야기가 될 것이라고 생각합니다.
잠시만, 이렇게만 이야기하면 무엇인 문제 제기가 되었는가 궁금할테니까 어떤 이야기였냐면 - 원래 의견을 써 주신 분의 글을 그대로 옮겨서 시작하겠습니다.
『보통 실무에서는 모집단(분석의 대상이 되는 집단)에서 n개씩의 샘플을 N회 복원 추출한다고 할 때 n이 약 30 이상의 너무 적지 않은 개수이고 시행 횟수 N이 많아질수록 매 회 n개를 뽑아 만든 평균들이 정규분포에 점점 가까워집니다. N은 무한히 할 수 없으니까 100~150번 정도라고 할까요."
은 잘못됐습니다. N이 아니라 n이 커져야 그 표본평균의 분포가 정규분포에 가까워지는 것이 맞습니다. n을 가만히 두고 N만 키우면 표본 평균의 분포가 정규분포에 '점점 더 가까워지는' 게 아니라, 정규분포와는 다소간의 차이가 있는 표본 평균의 분포를 점점 더 정확히 묘사할 수 있게 되는 것뿐입니다. n이 결정되는 순간 표본 평균의 분포도 이미 결정되는 것이고, N을 늘려도 그 분포가 정규분포에 더 가까워질 리가 없죠. 더 나아지는 것은 그 분포를 묘사함에 있어서의 정확성이라는 것입니다. 비유하자면 정규분포로부터 떨어진 과녁을 점점 더 정확히 맞힐 수 있게 되는 것이죠. 하지만 n (한 번 표집 할 때 모으는 표본의 크기)을 늘리면 과녁 자체가 점점 정규분포에 더 가까이 간다는 것입니다.』
위의 의견은 정확하게는 무슨 의미냐면, n이 정해지면 정규분포의 분산이 정해지니까, N과 무관하게 이미 확률분포는 가우시안으로 정해졌다는 의미입니다. 적확한 의견이고, 동의할 수 밖에 없습니다.
하지만, 어느 면에서는 중심극한정리에 대한 실무적인 설명을 저렇게 했으니, 읽는 사람은 그럴 수 밖에 라는 생각이 듭니다. 특히 "실무적"이라는 말이 어떤 의미인지를 풀어쓰지 않았던 것은 마치 어떤 여성한테, 밥 먹을래?라고 말해놓고 나중에 그건 널 좋아한다는 말이었어라고 너도 알거라 생각했는데..라는 듯한 마음대로 생각해 버리는 말 같은 그런 것이 아닐까 합니다. 사실 그렇게 받아들일 것이라고 알 턱이 있는가. 라는 점은 다시 한번 잘 생각해 볼만한 주제임에 틀림 없습니다.
그러니까, 그래도 조금은 이 이야기를 다시 한번 풀어보자면,
예를 들어, 극단적인 모집단 1, 2, 3, 4, 5의 5개 원소가 있는 작은 모집단에 대해서 n과 N을 변화시켜가며 그려보겠습니다. 저는 극단적이라는 말을 매우 좋아합니다. 그런 단어를 쓸 기회가 드물어서 아쉬웠는데 이번 기회에 쓸 수 있다니 이야기를 재미있게 진전시킬 수 있을거라 생각합니다.
참고로, μ = 3이로군요.
조금 헷갈릴 수 있는 부분이 있어서, n : 표본의 수, N : 표본 표집 횟수(복원추출횟수) 인 부분을 다시 한번 상기해 주세요.
첫 번째로는 단촐한 n = 10, N = 10
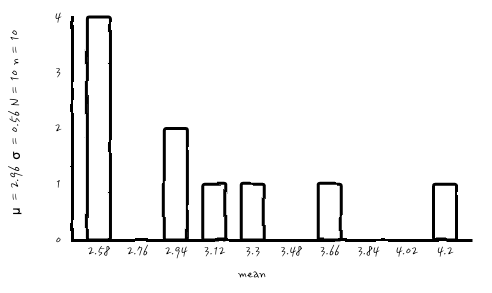
아, 표본수를 10으로 해서 10번 복원 추출해 보았더니, 이게 뭐야 싶습니다.
그래서, N은 고정으로 두고, n이 충분히 크면 가우시안이 된다고 했으니, n을 늘려가면 가우시안이 될런가. 한번 보시죠.
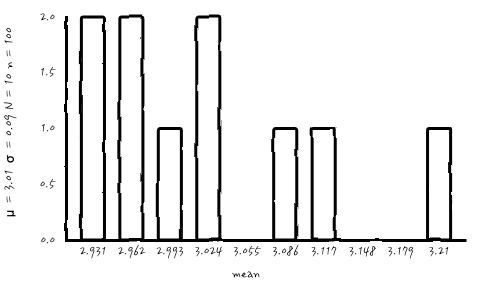
n = 100, N = 10
n = 1000, N = 10
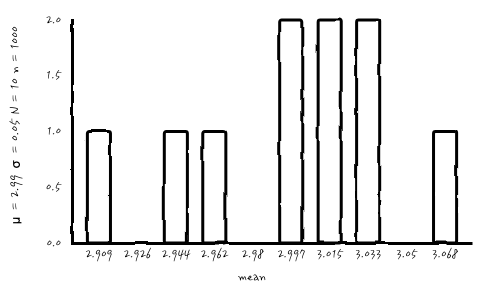
n = 10000, N = 10
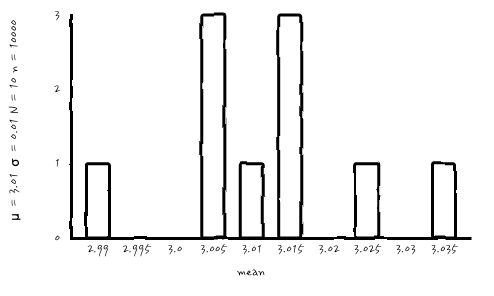
아무래도 복원추출횟수 N이 작다 보니, 표본 개수를 아무리 늘려도 가우시안처럼 보이질 않는군요. 중요한 사실은 가우시안 확률분포는 맞습니다. 가우시안 확률 분포로부터의 outcome이니까요. 하지만, 아무래도 실무적 눈으로 확인이 되지 않습니다. 진짜 가우시안인가?
그러면, n = 10정도의 작은 표본수와 복원 추출수 N을 100 정도로 충분히 키워서 한번 볼까요?
n = 10, N = 100
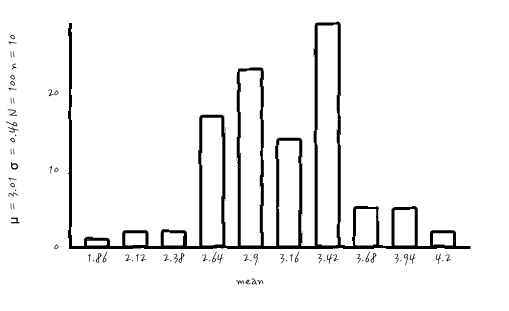
흠. 조금 더 뭔가, 봉긋한 분포가 나왔는데, 그럼 이번엔 신기하니까, N을 더 키우면 어떻게 될지 보자구요. n = 10, N = 1000으로 해보시죠.
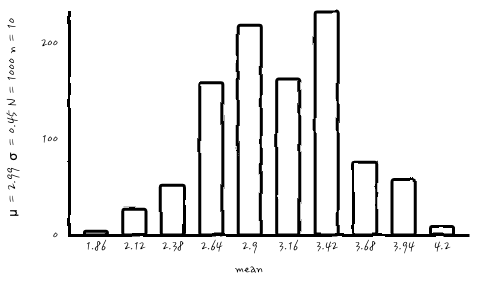
n이 작더라도, N 이 크니까 조금 가운데가 봉긋해 지네요. 그럼 복원추출을 10000번까지!!!
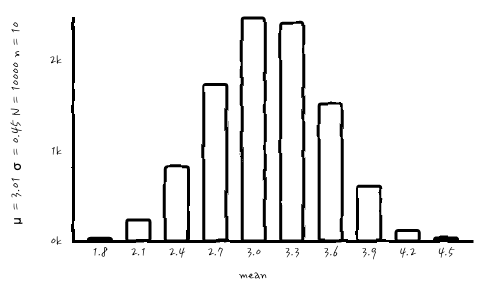
어랏 머죠. 가우시안처럼 보여져 버리네요. 이걸 원한 건 아니었지만, 어쨌든 점점 가우시안처럼 보이네요. 어쨌든 평균의 분포를 제대로 보려면 N이 어느 정도 커야 알 수 있겠군요.
자, 이번엔
n = 100, N = 100 으로 둘 다 키워보면,
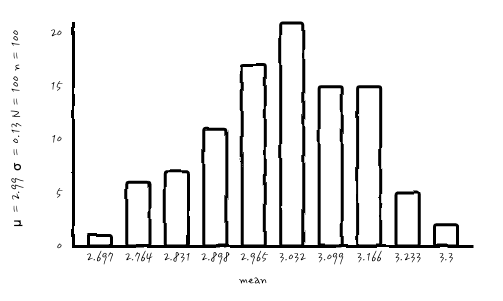
으헷, 이젠 어엿하게 가우시안처럼 보이네요. 와.
그러면, n = N = 1000, n = N = 10000, n = N = 100000으로 해서 한번 볼까요?
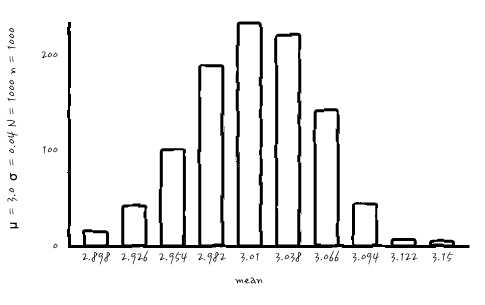
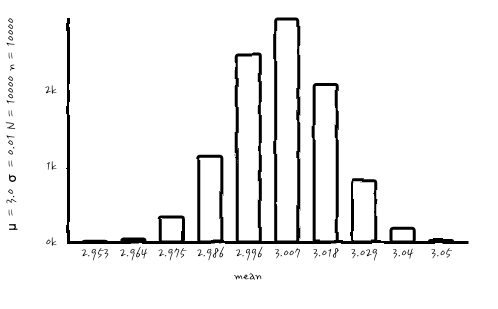
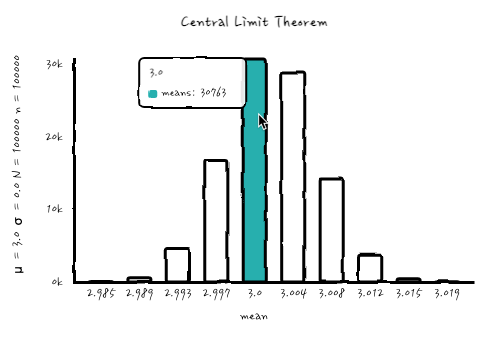
으핫, 이젠 어느 정도 늠름한 가우시안이 되어 버렸습니다. 심지어 마지막의 n = N = 10000인 경우에는 μ = 3이고, σ는 너무 작아서 0.0으로 표시될 정도로 작은 값으로 아주 샤프한 모양새를 보여줍니다. 토막정보로는 n=10000, N=1을 시행해서 평균을 내면 그 평균은 n = N = 10000 분포에서 한 가지 경우가 될 수 있겠습니다. 그러니까, 표본에서 평균을 내는 순간 그것은 중심극한정리에서의 가우시안의 outcome입니다. 이렇게 긴 이야기가 되어 버리다니.
원래의 글을 다시 정리하면,
보통 "실무"에서는 모집단(분석의 대상이 되는 집단)에서 n개씩의 샘플을 N회 복원 추출한다고 할 때 n이 약 30 이상의 너무 적지 않은 개수이고 시행 횟수 N이 많아질수록 n개의 평균들이 정규분포에 점점 가까워집니다. N은 무한히 할 수 없으니까 100~150번 정도라고 할까요.라는 말은 n이 충분히 크면 이미 그 상태에서 가우시안 확률분포를 갖지만, 이것이 진짜 가우시안인지 보려면 N(복원추출 횟수)을 어느 정도 많이 해야 가우시안처럼 보이고, 분석 대상의 데이터로 의미를 알아볼 수 있다. 는 의미로 받아들여주시면 전혀 터무니없는 말은 아니지 않은가.라고 생각합니다.
친절한 데이터 사이언스 강좌 글 전체 목차 (링크) - 
댓글