이제까지는 상관분석을 하기 위한 상관계수를 줄기차게 이야기했으니까, 겉도는 얘기는 그만하고, 상관분석이라는 것을 전격적으로 해봐야 하지 않을까 생각합니다. 실무적으로는 통계량을 보는 것 이외에 데이터가 어떤 느낌인지 확인할 때 가장 유용하게 사용하는 분석방법입니다. 특히 이 느낌에서부터 출발해서 회귀와 머신러닝까지도 다뤄볼 것이니까 이제는 정신 똑바로 붙들고 가야 합니다.
일단, 어느 정도의 상관이 있는지 상관 계수에 따른 상관에 정도를 보면 아래와 같은 정도로 판단하는 것이 일반적입니다.
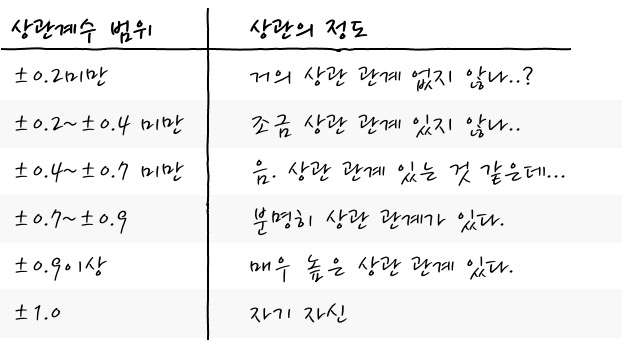
이런 구분이 있다고 해도, 뭐 절대적인 기준은 아닙니다. 그냥 그 정도구나로 생각해 주면 되겠습니다. 그러니까, 실무적으로는 0.4 이상이 되면 어느 정도 관계가 있지 않나 하고 판단하고, 0.9 이상이면 사실상 같은 변수라고 판단해도 무리가 없다고 생각해도 좋지 않을까 합니다. -1 경우 자기 자신은 아니지만 자기 자신에게 -를 붙인 것처럼 봐도 무방하겠습니다.
자, 그러면 바로 앞에서 본 상관계수를 이용해서 상관분석을 한번 해 보겠습니다.
예를 들어, 다음과 같은 데이터가 있다고 합니다. 어느 카페의 김원두 사장님이 매출에 상관관계가 있는 것이 무엇인지 알아내기 위해 열심히 고객의 (평가)Rating 데이터를 모았다고 합니다.
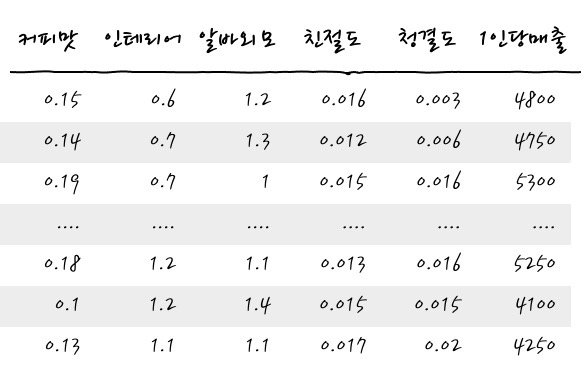
오, 그럴듯하게 잘 데이터를 잘 수집했군요. 이 데이터들이 어떻게 서로 관련이 있을까를 Correlation Analysis상관분석을 통해서 한번 알아내 보시죠. (1인당매출은 해당 답변 손님 1인의 매출입니다)
import padas as pd
df_data.corr() # df_data는 pandas dataframe임
뙇 곧바로 상관분석 결과가 나왔어요. 이미 해 보았으니까 이제는 신기하지는 않군요. 하지만 편리한 세상인 것만은 틀림없습니다.

이 결과를 구하긴 했는데, 결과를 어떻게 보느냐.하면. 보통의 표를 보듯이 행과 열로 보면 됩니다. 대각선으로는 자기 자신과의 상관이기 때문에 1이 나옵니다. 나머지는 당연히 다른 것들과의 상관관계죠. 그러니까, 당연하게도 대각선 1을 기준으로 위쪽과 아래쪽은 같은 값입니다.
이 상관분석표가 늘 눈에 잘 들어오질 않는데, 어떻게 읽으면 좋을지에 대한 팁을 보자면, 여기에서 독립변수와 종속변수를 염두에 두고 이야기할 것인데, 아무래도 회귀분석을 하기 전에도 도움이 되고, 인간의 인식이라는 것이 관심 데이터에 어느 것이 가장 관련이 있을까로 보면 쉽게 이해할 수 있으니까, 그런 식으로 읽어보려고 합니다. - 참고로 종속변수는 결과 y, 독립변수는 입력 x입니다. -

여기에서, 우리가 가장 관심있는 독립변수를 맨 앞에 놓으면 다른 독립변수와의 관계를 한눈에 볼 수 있습니다. 간단하죠. 이 경우에는 커피맛과 다른 값들과의 상관도를 보는 것입니다. 커피맛과 1인당 매출이 꽤 상관관계 높군요. 오. 어떻게 보면 당연한 결과이겠군요. 커피맛이 별로인데, 장사가 잘 되면 그것도 이상한 일이거든요.

그리고, 또 한가지 팁은 우리가 종속변수로 두고 싶은 변수를 맨 밑에 두면 또 편하게 볼 수 있겠죠. 곧 만나게 될 회귀 또는 머신러닝을 하기 위한 상관분석이라면 종속변수가 있다고 가정하고 데이터를 바라보면 보이는 것이 많아진다는 점. 이 경우에는 당연하게 사장님의 의도처럼 고객 1인당 매출을 종속변수처럼 취급한다면 어느 정도 의미 있는 분석적 접근이 되지 않을까 합니다.

쓱 훑어보니 1인당 매출과 커피맛, 알바외모가 양의 상관관계가 있는 것을 알 수 있습니다. 이것 또한 그럴듯한 이야기로군요. 그렇지만 여기에서 알바외모가 튀어나오다니 꽤나 흥미롭군요. 각각의 (독립)변수끼리의 상관계관계를 표에서 읽기에는 여전히 머리가 조금 지끈 거립니다.
자, 그러면 이런 표에서, (독립)변수끼리의 상관관계를 위쪽 값은 어지러우니까 잊자라고 한다면, 아래쪽 값들로만을 이용해서 ㄱ자 모양으로 값을 읽으면 편리합니다. 친절도를 예를 들면 ㄱ자 모양으로 읽는데 가로로 커피맛, 인테리어, 알바외모, 세로로 청결도, 1인당매출과의 관계를 읽는 방법도 있겠습니다. 이건 개인의 기호와 관련이 있으니까 그냥 옆으로 주르륵 읽어도 되지 않을까 합니다. 어쨌든 행이든 열이든 하나 기준을 잡아서 주르륵 읽는다는 것이 리빙포인트입니다.

자, 이제 어느정도 상관분석표를 읽을 수 있게 되었으니까요. 상관계수를 읽어봅시다. 어떤 것들이 서로 상관이 있는지 좀 살펴본다면 바로 전에 본 바와 같이 (커피맛-1인당매출), (알바외모-1인당매출) 정도가 꽤나 상관이 있는 것 같군요. 뭐 어느 정도는 상식선에서 관계가 나온 것 같습니다. - 알바 외모가 1인당 매출에 영향을 미친다니 이걸 데이터로 확인하게 되다니 그냥 그렇지 않을까 정도였는데 말이죠 -. (독립)변수끼리는 작은 관계이긴 하지만 인테리어-청결도가 양의 관계, 알바외모-청결도가 음의 관계를 보이긴 하는군요. -, (독립)변수와 (종속)변수의 관계가 그런 것이 있네요. 오. 이거 뭔가 재미있는 분석이 될 것인지 흥미진진합니다. 알바외모가 좋을수록 청결도가 안 좋다니. 사실은 알바외모라기보다는 알바의 친절도가 아닐까 생각도 드네요. 청결보다는 친절에 더 시간을 많이 써야 하는 것 아닐까? 뭐 그런 정도의 추론입니다.

그럼 지금 하고 있는 것은 통계분석이니까요, 당연히 검정결과 즉, p value도 보면 좋겠는데, 이것은 어떻게 보는가 하면, 다음과 같이 계산하면 간단하게 나옵니다.
df_data.corr(method=lambda x, y : pearsonr(x,y)[1])
pearsonr의 두번째([1]) 결괏값은 p value이기 때문에 corr 분석표에 상관계수 대신에 p value로 채워줍니다.

자, 어떤가요? 이 p value table에서 꽤나 Significant 한 값들은 커피맛-1인당매출, 알바외모-1인당매출이 그렇군요. 음. 일단 대충 상관도가 0.1보다 크면 p value도 유의미하다고 나오는군요. 뭐, 이것도 상식적입니다. 굳이 해석하자면 1인당 매출에 관련하여 상관도가 큰 커피맛과 알바외모가 중요한 요인이 되겠군요. 막상 알바외모와 커피맛의 Correlation이 작아서 다행입니다. `
참고로, r과 p value를 합쳐서 보면 논문등에서 상관계수의 오른쪽 위에 *이 붙어서 나오는 경우가 있는데, *는 95%, **는 99%, ***는 99.9% 유의수준으로 유의하다는 의미입니다.

그러니까, *이 많을 수록 더 Extraordinary 하다는 의미인데요, 이걸 보고 싶다면, 이걸 해주는 자동으로 해 주는 패키지가 있는데, 이미 ANOVA에서도 한번 사용해 봤던 pingouin package입니다.
import pingouin as pg
pg.rcorr(df_raw)

이런 식으로 왼쪽 아래쪽은 r값을 오른쪽 위쪽에는 유의수준을 표시해 줍니다. 아이디어가 꽤 쌈빡합니다요. 편리한 결과의 관리라는 관점에서는 말이죠. - 아이디어가 쌈빡하긴 하지만 여전히 한 번에 보기 어려운 점은 어쩔 수가 없군요 -
자, 그러면 이렇게 보긴 했는데 이제 어쩌란 말인가? 하는 생각이 드는 것이 당연한 의문의 순서라고 생각합니다. 서로 관계가 있다는 것을 알아서 어디에 쓰지.
대충의 그 용도는 보통 회귀분석을 할 때, 회귀만 하면 되는데, 그 전에 상관분석을 하게 되는 경우가 많이 있습니다. 분석 후 어떤 시사점을 얻을 수 있는가 하면 크게는 다음의 2가지 경우가 있습니다.
➊ 독립변수들끼리 너무 서로 상관관계가 큰 경우에 어떤 현상이 일어나는데, 그 어떤 현상이라는 것이 서로 상관관계가 큰 변수끼리 다중공선성을 일으킬 가능성이 매우 높습니다. 여기에서 다중공선성이란 말 자체가 어려운데 독립변수끼리 같이 움직이긴 하지만 당연히 비슷하게 같이 움직이는 독립변수 중에 대표적인 1개 독립변수 하나만 있으면 대충 어떤 식으로 회귀 모델에 그 변수가 기여하는지 알 수 있겠는데, 이것들이 모두 모델에 포함되면 독립변수 하나만 있을 때 보다 그 두 개 변수의 합 때문에 그 변수의 합의 분산이 1개 있을 때 보다 커져버려서 회귀 모델의 계수의 분산을 크게 할 수 있다는 뜻입니다. 그러니까 회귀 분석을 하게 된다면 이런 일이 벌어질 것인가? 에 대한 Intuition을 얻을 수 있는 방법론이라고 생각하면 좋습니다.
➋ 독립변수들이 종속변수와 너무 관계가 없어도 좀 어렵습니다. 어느정도는 관계가 있어줘야 회귀결과에도 반영될 수 있겠습니다.
이게 아주 중요한 시사점이고, 여기에 하나 더 덧붙이면 금상첨화라고 할 수 있겠는데, 각각의 상관계수가 검정을 통해서 유의미한 값인지를 짚어볼 필요가 있겠습니다. 상관계수는 큰데 유의미하지 않으면 보통 표본의 크기가 작아서 그런 것 아닌가? 정도의 Intuition을 가지고 있으면 좋겠습니다. 시사점들이 회귀분석을 하게 된다면, 이라는 가정으로 그렇다고 하긴 했지만 그건 사실 나중에 볼 일이고, 상관분석을 통해 일단 변수들 간의 관계를 아는 것은 무조건 유용합니다.

어쨌든 상관분석을 통해서 얻을 수 있는 교훈은 Feature Extraction, Feature Selection이라는 것을 할 수 있다는 점 입니다. 여기에서 Feature Selection은 적당한 Feature를 고르는 것이고, Feature Extraction이라는 것은 다르게 표현하면, 차원 축소라고도 할 수 있는데, Feature Selection은 데이터중에서 우리가 관심 있는 종속변수 y가 있는 경우에는 y와 대충~ 상관이 적당히 있는 것들만을 - 이것에 대해서는 정답이 없음 - 골라서 거지같이 관련이 적은 컬럼을 삭제하여 독립변수의 수를 줄여 차원을 축소한다는 의미이기도 하고, Feature Extraction의 경우에는 종속변수 y가 없는 데이터라면 PCA주성분 분석을 이용해서 어떤 것이 이 데이터중에서 주 성분인지를 알아내어 독립변수를 합치는 방법으로 차원을 축소하기도 합니다. 여기에서 Feature는 데이터의 컬럼을 의미한다고 보면 되겠습니다. 어렵게 이야기 하긴 했지만 결국 분석을 잘하기 위해 중요한 Data를 고르는 과정이라고 생각하면 됩니다.

보통 Regression을 할 때, 다중공선성을 제거하기 위해서 PCA주성분분석을 통해서 차원 축소를 한다고 주장하기도 하는데, PCA는 종속변수가 없는 경우에 사용하니까, 그다지 의미가 없을 수 있고, 상관분석을 통해 상관도가 큰 (독립)변수를 제거해야 한다는 말도 있지만, 오히려 VIF(Variance Inflation Factor) 분석을 하는 편이 나을 수 있습니다. - 이런 용어를 남발해서 미안합니다만 어차피 나중에 볼 거 지금 그런 게 있구나 정도를 알아두는 것도 좋다고 생각합니다. 말 그대로 변량을 증가시키는 팩터를 찾는 분석입니다. - 하지만, 예측을 목적으로 하는 딥러닝 등을 할 때에는 다중공선성이 뭐다냐? 난 모르겠다고 무시하고 Feature를 마구마구 떄려넣어서 학습 데이터와 모델을 구성하는 경우도 많습니다.

상관분석표를 보는데 pandas의 method를 이용하면 조금 쉽게 결과를 볼 수 있는 방법이 있습니다.
1) df_data.corrwith(df['1인당매출'])
2) df_data['1인당매출'].corr(df_data['알바외모'])
이 두 개가 어떤 식으로 쓸 수 있는 것이냐면
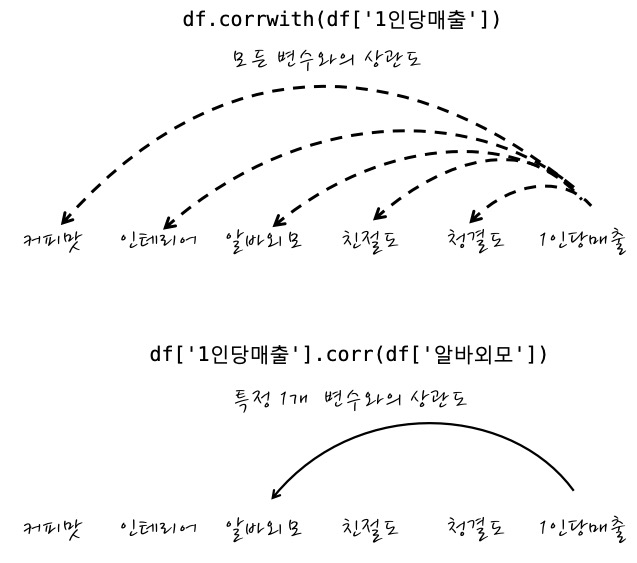
이런 식이고요. df는 DataFrame입니다.
실제 확인해 보면 말이죠,
df_data.corrwith(df_data['1인당매출'])
>
커피맛 0.831680
인테리어 -0.066088
알바외모 0.473430
친절도 0.045661
청결도 -0.184140
1인당매출 1.000000
df_data['1인당매출'].corr(df_data['알바외모'])
>
0.4734297984730023
이런 식입니다. 뭐 이런 방법도 있다 정도의 정보로 드려요.

실제 상관도를 확인하면서 이게 선형인지를 확인하지 않으면 조금 곤란할 수 있으니까, 늘 관심이 있는 변수끼리는 Scatter Plot으로 확인하면 좋습니다. 예를 들어, 1인당 매출과 알바외모가 실제로 선형 관계인지를 Scatter Plot으로 그려보면,
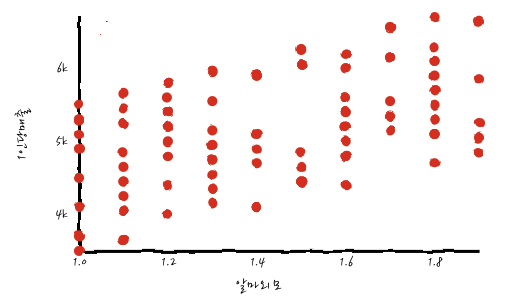
정말 알바외모-1인당매출이 선형 관계를 가지고 있는 것처럼 보이는군요. 다만, 이걸로 예측 모델링을 한다면 초큼 애매할 수도 있겠다는 느낌적인 느낌이 있네요.
 친절한 데이터 사이언스 강좌 글 전체 목차 (정주행 링크) -
친절한 데이터 사이언스 강좌 글 전체 목차 (정주행 링크) - 

댓글