뜬금없이 유전자 알고리즘이라는 걸 이용해서 어떤 문제를 풀어보려고 합니다. 보통 줄여서 유전알고리즘이라고 많이 부릅니다.
유전자 알고리즘이란, 영어로는 Genetic Algorithm이라고 해서 별건 없고 유전자 벡터 모음에 대하여 자연스러운 교배와 진화를 통해서 최적의 해인 유전자 벡터를 구할 수 있다는 뭐 그런 겁니다. 뭔가 좀 있어 보이죠. 조금 더 자세하게 이야기하자면 생물 유전학에서 부터 시작한 생물학적 진화에 바탕을 둔 통계학적 알고리즘이라고 생각하면 좋겠습니다.
이걸 해 두면, 컴퓨터가 어떤 식으로 문제를 풀어가는지를 눈치채는데 도움이 많이 될 것이라 생각합니다.
우선 유전알고리즘이 뭔지부터 좀 보시죠.

유전알고리즘은 이런 식입니다. 그냥 유전자를 진화시키는 것과 비슷한 느낌인데요, Pseudo 코드로 보면 다음과 같습니다.
⓵ 최초의 유전자 집합을 생성 while (True) { ⓶ 유전자 집합을 이용하여 성능을 측정. 만족스러우면 break ⓷ 똑똑한 유전자들을 선발, 나머지 버림 버려진 유전자 자리를 ⓸ 교배 또는 ⓹ 돌연변이 생성 (Mutation) 또는 ⓺ 완전히 새로운 유전자 생성 로 대치 }
이렇게 한 후, 한번 루프를 돌 떄마다 1 세대를 진화했다고 표현합니다. 멋지군요. 잘 보면 똑똑한 유전자를 선발해서 교배하거나 돌연변이들을 만들어내는 것을 몇 세대를 계속하다 보면 가장 좋은 유전자 배열이 된다는 것이 아이디어입니다.
이해를 잘 하기 위해, 돌연변이와 교배에 대해 조금만 이야기하자면,

돌연변이는 우성인자를 선택해서 일부를 조금 바꾸는 것이고요,

교배는 우성인자끼리 딴딴따단~♪ 결혼시키는 것입니다.
어쨌든 아. 그렇군요!라고 해 봤자, 그래서 어떤 식으로 구현한다는 거지? 싶을 테니까 실전적인 코드를 한번 구현하면서 문제를 한번 풀어보겠습니다. 이번에는 본격 코드를 통한 이야기를 좀 하려고 하니, 이를 꽉 물고, 똥꼬에 힘 주세요.
실전예)
여자친구의 휴대폰의 비밀번호 6자리를 풀어보겠습니다. 이건 순전히 웃자고 하는 예니까 심각하게 생각하진 말아 주세요. 후후. 이걸 brute force 하게 막무가내로 눌러서 알아내려면 10의 6 승개만큼 눌러봐야 하겠죠. 100만 번입니다. 뭐 언젠간 알아낼 수 있겠군요. 1초에 한 번씩 하면 최대 23일 정도면 알아낼 수 있겠습니다. 하지만, 이걸 유전 알고리즘을 통해서 최적해를 구해보면 생각보다 쉽게 풀립니다. 놀랍지요?
큰 그림을 이해하기 위해 일단 조금 더 자세한 Pseudo Code를 보면 이렇습니다. 이 유전알고리즘은 여자친구 비밀번호 문제 외에도 계속 재사용가능하도록 설계를 하려고 합니다.
''' 필요 Parameters : 엘리트 랭킹, 확률(mutate, breeding, crossover), 최대 세대, Solution이 가질 수 있는 값 범위 (domain), 전체 Population 수 ''' def 유전 알고리즘 : def 유전자 생성 breeding (vector) : def 돌연변이 mutate (vector) : def 교배함 crossover (vector) : 세대를 거쳐 진화 iteration of generation { 유전자들의 성능에 따라 랭킹을 만들고, 엘리트 랭킹보다 안좋은 것은 버림 확률에 따라 mutate, breeding, crossover를 하여 버린 유전자 집단을 대치 }
이렇게 보니 조금은 코드를 어떤 식으로 짜야할지 그림이 그려지지 않나요. 그런데, 유전알고리즘에 너무 집중한 나머지 진짜 중요한 부분이 있는데 그걸 놓치면 안 됩니다. 그게 뭐냐면 유전자들의 "성능"에 따라 똑똑한 엘리트 유전자들을 고른다는 점입니다. 그러니까 우리는 유전자의 성능을 측정할 수 있어야 합니다. - 사실 여자친구의 비밀번호를 풀어낸다는 설정에서 유일한 비현실적인 부분입니다. 이 성능을 측정할 수 없다면 사실 다 무용지물입니다. 그렇지만 머, 측정할 수 있다고 합시다요. - 어쨌든 유전알고리즘을 이용하여 비밀번호를 입력했을 때 해당 유전자의 성능을 판단하기 위해서 cost라는 걸 정의하는 편이 좋겠습니다. cost란 얼마나 정답과 다른가를 정의한다고 보면 되겠습니다.
Cost를 정의하는 데 더 좋은 방법들도 많이 있겠지만, 입력한 비밀번호와 정답 비밀번호를 각 자리에서 비교하고 값이 틀릴 때에는 +1 cost를 주는 것입니다. 그러니까 모든 자리가 틀렸을 경우 최대 6점이 되겠군요. 그리고 입력한 비밀번호에 대하여 각 자리의 숫자를 검사해서 해당 숫자가 비밀번호 중에 아예 없으면 +3 cost를 추가하는 방향도 괜찮다고 생각합니다. 이렇게 가보시죠.
자, 그렇다면 이제 마음의 준비는 끝났습니다. 후다닥 유전알고리즘을 구현해 보시죠. 실행은 마지막의 find_password()를 보면 되고, 참고로 domain은 유전자가 가질 수 있는 범위입니다. 즉 비밀번호의 범위라고 볼 수 있겠습니다.
import random def geneticoptimize(domain,costf,popsize=200,step=1, mutprob=0.5,elite=0.2,maxiter=1000,crossprob=0.4): # domain range에 들어오지 않으면 clamping def clamp(val, minval, maxval): if val < minval: return minval if val > maxval: return maxval return val # 새로운 유전자 낳기 (Breeding) def breeding(vec) : return [random.randint(domain[j][0],domain[j][1]) for j in range(len(domain))] # 돌연변이 만들기 (Mutate) def mutate(vec): i=random.randint(0,len(vec)-1) mutate=random.randint(0,len(domain)-1) if vec[i] > domain[i][0] and vec[i] < domain[i][1] : # domain에 적당하면 # vec i 번째 값을 step값 만큼 더하거나 뺌 이건 해도되고 안해도 됨. if random.random()<0.5 : mutate = clamp(mutate + step, domain[i][0], domain[i][1]) else : mutate = clamp(mutate - step, domain[i][0], domain[i][1]) return vec[0:i] + [mutate] + vec[i+1:] else : return vec # 교배하기 (Crossover) def crossover(r1,r2): i=random.randint(1,len(domain)-2) # -2를 해 줘야 최소한 1개 남음 return r1[0:i]+r2[i:] # 최초 유전자 집합 생성 pop=[] for i in range(popsize): vec=[random.randint(domain[j][0],domain[j][1]) for j in range(len(domain))] pop.append(vec) # 똑똑한 유전자 개수 설정 topelite=int(elite*popsize) # 진화 루프 (세대) for i in range(maxiter): scores=[(costf(v),v) for v in pop] # (성능, 유전자) 튜플로 관리 scores.sort() # Cost가 낮은 것부터 유전자 Sort ranked=[v for (s,v) in scores] # Cost가 0이면 진화를 멈춤 if scores[0][0] == 0 : break # 똑똑한 유전자 선발 pop=ranked[0:topelite] while len(pop)<popsize: prob = random.random() if prob<mutprob: # 돌연변이 (Mutate) c=random.randint(0,topelite) m = mutate(ranked[c]) # MUTATE pop.append(m) elif prob>1-crossprob : # 교배 (Crossover) c1=random.randint(0,topelite) c2=random.randint(0,topelite) m = crossover(ranked[c1],ranked[c2]) pop.append(m) # CROSS OVER else: # 새 유전자 생성 breeding m = [random.randint(domain[j][0],domain[j][1]) for j in range(len(domain))] pop.append(m) # 현재 1등의 cost 출력 print (scores[0][0], end=" ") print ("".join(map(str,scores[0][1])), end=" ") # 1등의 cost, 세대 출력 print ("".join(map(str,scores[0][1])), end=" ") print (scores[0][0], end=" ") print ("Terminated at Generation %d" %(i+1), end=" ") print (["".join(k) for k in ([str(x) for x in ranked]) ] ) return scores[0][1] # return solution def cost(sol): correct_pwd = "728398" # 정답 여자친구 핸드폰 비밀번호 total_cost = 0 for i in range(len(correct_pwd)) : if correct_pwd[i] != str(sol[i]) : total_cost += 1 if str(sol[i]) not in correct_pwd : total_cost += 3 return total_cost def find_password() : domain = [(0,9)]*6 # 0~9까지의 6자리 비밀번호 solution = geneticoptimize(domain, cost) final_password = "".join(map(str,solution)) find_password()
사실 코드를 이렇게 전부 늘어놓고 보는 것을 별로 좋아하지는 않지만, 그래도 기계는 어떻게 답을 찾아가는가 -학습하는가 -를 보는 첫 번째 코드이기도 하고, 엄청 길지 않으니까, 전체 코드를 한번 보는 것도 나쁘지 않다고 생각합니다.
find_password() 안에서
solution = geneticoptimize(domain, cost)
부분이 중요한데, geneticoptimize가 유전알고리즘으로 최적해를 구하는 것이고, domain이 유전자가 가질 수 있는 범위, cost가 어떤 식으로 cost를 계산할 것인가에 대한 함수정의, solution이 최종 해 - 가장 똑똑한 유전자 -입니다. 이 표현을 잘 기억해 주세요.
어쨌든 find_password()를 통해 유전자를 진화시킨 후에 결과를 보면 조금 놀라운데, 유전자 중 가장 우월한 유전자가 진화하면서 cost가 어떻게 줄어드냐면
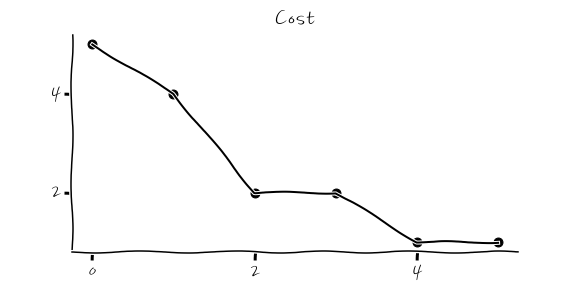
이런 식으로 줄어듭니다. 결국에는 Cost가 0이 되면서 비밀번호를 찾아냅니다. 단 5세대 만에 비밀번호를 찾아냅니다. 놀랍지 않나요? - 매번 할 때마다 달라지긴 하지만 금방 찾아냅니다. - 써프라이즈.

처음으로 코드라는 걸 다뤄봤는데, 할만할 거라 생각합니다.라고 희망적으로 생각해 봅니다.

유전알고리즘을 이곳저곳에 이용해서 설명할 요량이기도 하고, 잘 알아두면 꽤나 유용한 알고리즘입니다. 이번 기회에 잘 알아두고 해를 찾는 컨셉에서 자주 써먹을 계획입니다.
 친절한 데이터 사이언스 강좌 글 전체 목차 (정주행 링크) -
친절한 데이터 사이언스 강좌 글 전체 목차 (정주행 링크) - 

댓글