신뢰수준을 높이면 신뢰구간은 넓어진다. 사기 같은 이야기

통계에서의 신뢰라는 것은 무엇일까 생각해 보는 짧은 이야기. 신뢰한다는 의미는 믿는다는 의미와 정확하다는 의미가 같이 Mingle 되어 있다고 생각합니다. 물론 이건 개인적인 생각일 수 있다는 점이 걸리긴 하지만, 그래도 그런 느낌이나 경향이 있는 것 아닌가 생각합니다. 꼭 그렇지만은 않다고 생각한다고 해서 눈총을 주지는 마세요.

Estimation추정을 하면서 Parameter모수를 구간 추정을 할 때에는 신뢰수준에 의한 신뢰구간이 주요한 추정 결과입니다.

한 가지 재미있는 이야기는 신뢰수준이 95%일 때와 99%일 때, 어느 것이 더 정확한 추정일까요? 일반적으로 정확하다고 함은 precise 하다는 뉘앙스인데 같은 느낌일까요.

일반적인 느낌으로는 예를 들어 신뢰도 95%로 추정한 경우에 10~20 사이에 평균이 들어 있다면 신뢰도 99%로 추정하게 되면 14~16 사이에 평균이 들어 있을 것이다라고 표현해야 할 것 같은데 말입니다. 그게 개인적인 느낌입니다만.

먼저 예를 들었던, 평균 추정 문제를 다시 한번 확인해 본다면 말이죠,

어떤 온도를 측정하는데, 표본평균 20˚C를 관측했던 문제였는데요, (표준오차 5)

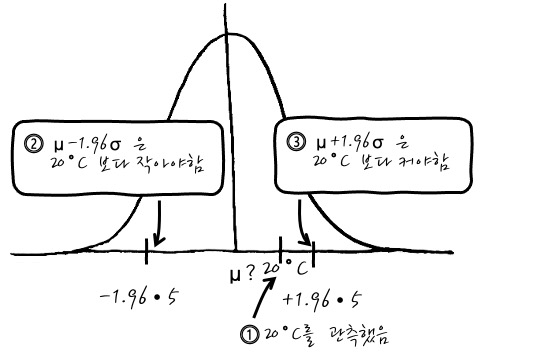
그러니까, 95% 신뢰수준으로 아래처럼 upper bound와 lower bound를 계산해서 예측했었습니다.

$$
\begin{align*}
\mu + 1.96\cdot 5 \geq 20℃ \\
\mu - 1.96\cdot 5 \leq 20℃
\end{align*}
$$

계산해 본 95% 신뢰구간은 $ 10.2 \le \mu \le 29.8 $ 이었습니다.

그렇다면 이걸 99% 신뢰도로 다시 구하게 되면 어떻게 될까요?

$$
P(\mu-2.58 \sigma<\bar{X}<\mu+2.58 \sigma)=99 \% \\
P(\mu-1.96 \sigma<\bar{X}<\mu+1.96 \sigma)=95 \%
$$
이니까,

$$
\begin{align*}
\mu + 2.58\cdot 5 \geq 20℃ \\
\mu - 2.59\cdot 5 \leq 20℃
\end{align*}
$$ 이 됩니다.

계산해 본 99% 신뢰구간은 $ 7.1 \le \mu \le 32.9 $ 가 됩니다.

어? 99%신뢰도로 하면 신뢰구간이 더 넓어지는군요? 왜 때문이죠?

통계에서는 모르는 것 투성이기 때문에 더 정확하게 예측한다는 의미는 더 넓은 범위를 포함해 버리면 예측한 것이 덜 틀릴 가능성이 있다. 확률적인 의미를 따지자면 당연한 얘기입니다만, 뭐 그런 얘기입니다.

이걸 처음에 본 소감은, 아니, 이런 식이면 100% 정확한 방법은 -∞ ~ +∞ 사이에 있다고 하면 되는 것 아닌가? 왜 이렇게 어려운 짓을 하고 있지?라는 뭐랄까 실망감이 있었다고나 할까요? 뭐, 그랬습니다.

하지만, 이런 신뢰구간이지만, 이것을 이용해서, 다른 것들, 특히 검정 같은 것들이 가능해 지니까, 추정은 사기 아닌가.라는 생각을 조금은 잊어버렸으면 합니다.