데이터를 다루려고 보면 통계를 할 때, 확률과 선형대수가 필수라는 이야기를 많이들 합니다. 아니 데이터를 다루는데, 갑자기 웬 선형대수인가라고 생각이 발끈 들지만, 어쨌든 많은 데이터를 한방에 다루기 위해서는 선형대수가 도구로써 의미가 있기 때문이지 정도로 이해하면 좋겠습니다. 게다가 선형대수라고 하면 너무 거창하니까, 그냥 행렬곱과 데이터와 행렬의 관계 정도만 들여다보면 여러모로 쓸모가 있지 않을까 생각합니다.
일단, 행렬이 어려운 이유는 곧바로 계산하기 어렵기 때문인데, 특히 행렬의 곱을 어떻게 해석해야 할지도 막연한데, 곱하는 방법도 만만치 않습니다. 행렬은 테이블을 보기 좋게 정리한 것이 아니라, 연산을 편리하게 하기 위해서 만들어 놓았다는 사실을 알고 있다면 조금은 덜 헷갈리지 않을까 합니다.
행렬은 행과 열로 이루어져 있는 숫자의 뭉탱이인데, 영어로는 행은 Row, 열은 Column입니다. 영어로는 Matrix라고 부르는데, 행렬만큼은 한국어가 훨씬 쉬운 용어가 아닌가 생각합니다. 통계를 하면서 늘 용어가 와닿지 않아서 어려웠는데, 정말 잘 지은 것 같습니다.
행과 열은 이렇게 이루어져 있고요. 무엇이든 행과 열의 순서로 Numbering을 합니다. 호. 심지어는 행렬의 크기를 따질 때도 행의 갯수, 열의 개수 순서로 따집니다.
이걸 머리에 꼭 집어넣고 있으면 매우 편합니다.
일단 이 숫자의 뭉탱이 행렬을 얘기할 때 행렬의 용도에 따라 다르게 바라보면 이해하기가 편한데, 어떤 식이냐면, 데이터는 벡터의 모음라고 생각하고, 그것을 가지고 뭔가 계산을 하기 위한 행렬은 벡터를 변환하기 위한 숫자의 뭉탱이라고 행렬 생각하면 생각하기 편합니다.
일단 벡터가 나왔으니, 벡터는 그냥 데이터 하나라고 생각하면 좋겠습니다. 행으로 이루어져 있든, 열로 이루어져 있든 말이죠.
행이나 열로 데이터를 표현한 것인데요. 간단하죠?
자, 여기에서 행렬을 시작하면 행렬의 곱셈을 시작하면 그나마 쉽게 행렬 연산을 이해하기 좋습니다.
일반적으로, 행렬의 곱은
이런식 인데요. 그래서요? 라는 의문이 생깁니다. 왜 이렇게 어렵게 곱셈을 하는 것인가요? 게다가 보통 행렬의 곱셈을 따질 때, (k×n)×(n×m) 을 계산하면 (k×m) 의 행렬이 나온다고 하잖아요? 이게 머리로는 알겠는데, 금방 그려지질 않거든요.
이걸 빨리 머리속에 그려보는 일을 해 보시죠. 이게 행렬곱을 행렬끼리 곱한다고 생각하면 여간 복잡해지는 것이 아닙니다. 행렬곱이라기보다는 행렬과 벡터의 곱으로 생각하면 훨씬 편리합니다. 특히 행렬을 벡터를 변환시키는 어떤 선형함수라고 생각하면 오히려 쉽게 느껴집니다.
선형대수를 보면 우리 보통
$$\mathcal{L} : \mathcal{R}^n → \mathcal{R}^m $$ 이런 식의 Notation을 볼 때가 있는데, 이것은 n차원의 데이터를 m차원으로 보낸다는 의미인데요. 이 의미는 행렬이 n차원의 입력 벡터를 m차원의 출력 벡터로 만든다고 생각하면 됩니다.
이걸 일반적인 이야기로 이야기 하면,
$$X → Y $$ 화살표 → 이것에는 일정한 규칙이 있고 (행렬), 그 규칙에 의해서 Y로 변경되는 것을 사상이라고 부르고, 사상은 규칙 또는 function(함수)이라고 생각하면 되겠는데, 그러니까 행렬이 함수라고 생각한다는 방식입니다.
그러면 이걸 행렬에서 한번 따져보면 벡터는 n차원의 입력이고, 그 벡터를 행렬을 통해서 다른 차원 m으로 보낸다고 생각하면,
➊ n차원 행벡터를
➋ m개의 열을 가진 행렬에 넣으면
➌ m차원의 행벡터가 나온다.
이런 식이죠. 저는 이걸 기억할 때 누워서 들어가면 누워서 나온다고 기억하고 있는데, 이것이 누군가에겐 도움이 될지 모르겠습니다. 자, 그러면 여기에서 아주 중요한 변형을 소개하는데, 행 벡터가 여러 개 있으면 어떻게 될까요?
그 이야기는 행벡터 k개를 넣는다고 할 때,
➊ k개의 n차원 행 벡터를
➋ m개의 열을 가진 행렬에 넣으면
➌ k개의 m차원의 행벡터가 나온다.
짜잔! 이런 의미입니다. 아하 간단하네요! 그러면 이 행렬의 의미도 살펴봐야 하겠지요? 행렬의 곱셈을 잘 아시겠지만, 입력의 행 벡터에 nxm행렬의 열에 곱해져서 나오지요? 그러니까,
이런 식이 되는 이야기 입니다. 중간의 행렬이 뭔가 입력 벡터의 차원을 한꺼번에 바꿔주는 일을 하는군요. 호.
그러면, 이 행렬은 도대체 어떻게 이루어진 것일까를 한번 잘 살펴보면 좋겠는데요, $w_{11}, w_{21}, w_{31} \cdots w_{n1}$ 의 의미를 잘 살펴보면, 출력의 첫 번째 row를 만들 때, 각각의 입력 행 벡터가 출력 벡터에 얼마나 Contribution 하는 지를 알려줍니다. 그러니까, $w_{11}$은 입력 행 벡터의 첫 번째 데이터가 출력 행 벡터의 첫 번째 데이터에 기여하는 바이고, $w_{21}$은 입력 행 벡터의 두 번째 데이터가 첫 번째 출력 행 벡터에 얼마나 기여하는지를 나타냅니다.
결국,
$$y_1 = w_{11}x_1 + w_{21}x_2 + \cdots + w_{n1}x_n$$
요런 느낌적인 느낌이 되겠습니다.
이렇게 보고 나니, 별거 아니지요? 그냥 행 벡터를 행렬을 통해 다른 차원의 행벡터로 변환시킨다고 보면 좋겠는데요. 방금, 행벡터를 다뤄보긴 했지만, 대부분의 수학적 기법들이 열 벡터를 행렬로 변환시켜 다루는 일이 많이 있어서, 더 중요한 열 벡터와 행렬의 곱셈의 관계를 똑같은 방법으로 다뤄보겠습니다.
기억을 더듬어 보면 회전 행렬 같은 경우에는
$
\begin{equation*}
\begin{bmatrix}
x' \\
y'
\end{bmatrix} =
\begin{bmatrix}
cos\theta & -sin\theta \\
sin\theta & cos\theta
\end{bmatrix}
\begin{bmatrix}
x \\
y
\end{bmatrix}
\end{equation*}
$
요런 식으로 열 벡터를 열 벡터로 변환하는 것들도 많이 있었죠.
행 벡터와 마찬가지로 n차원 열 벡터를 m×n 행렬에 넣으면 m차원 열 벡터가 나온다는 뭐 그런 시덥지 않은 이야기입니다.
이것도 마찬가지로 열벡터를 k개 두면 무슨 일이 일어날까요? k개의 m차원 열벡터가 나오겠군요. 후후
똑같군요. 그러면, 똑같이 m×n 행렬을 조금 더 자세히 살펴볼까요?
아하. 그러면 조금 더 자세하게 행렬을 살펴보면,
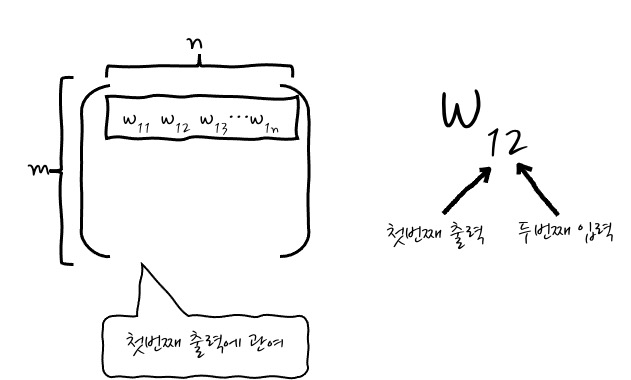
뭐든지 거꾸로 되어 있군요. 조금 어질어질하군요.
$$y_1 = w_{11}x_1 + w_{12}x_2 + \cdots + w_{1n}x_n$$
이런 의미입니다. 후후.
자, 다시 한번 정리하면! - 저는 행 벡터는 엄청 쉬운데, 열 벡터는 좀 어렵더라고요 라고 미리 고백을 해 두면 마음이 편할 것 같습니다 -
이런 모양새인데요. 곱셈에 대해서 기억할 것은 아래의 딱 3개입니다.
- 먼저 입력이 무엇인지부터 빨리 캐치하거나, 설정하여,
⓵ 누워 들어가면 누워 나오고, 서서 들어가면 서서 나온다.
⓶ 누워 들어간 개수만큼 누워 나오고, 서서 들어간 개수 만큼 서서 나온다. 이 의미는 입력 개수와 출력 개수가 같다는 뜻입니다.
⓷ 함수로서의 행렬은 각 열 또는 행이 결과 벡터의 해당 열 또는 행의 계수(Weight/ Coefficient)가 된다.
이렇게 빨리 머릿속에 그려 넣어야 합니다.
직접적인 예로 한번 예를 들면 조금 더 낫겠다 싶어서 한 번만 해보겠습니다.
열 벡터의 경우 3×2 행렬이 있다면 곧바로 2차원 열 벡터를 넣었을 때, 3차원 열 벡터가 나오겠군 하고 곧바로 상상 가능하면 됩니다. 그러니까, 어떤 행렬을 보았을 때에는 재빠르게 입력을 열 벡터나 행 벡터로 고정하고 생각하면 곧바로 답이 보입니다.
$
\begin{equation*}
\begin{bmatrix}
w_{11} & w_{12} \\
w_{21} & w_{22} \\
w_{31} & w_{32} \\
\end{bmatrix}
\begin{bmatrix}
x_1 \\
x_2 \\
\end{bmatrix}
=\begin{bmatrix}
y_1 \\
y_2 \\
y_3
\end{bmatrix}
=\begin{bmatrix}
w_{11}x_1 + w_{12}x_2 \\
w_{21}x_1 + w_{22}x_2 \\
w_{31}x_1 + w_{32}x_2
\end{bmatrix}
\end{equation*}
$
2차원 벡터 입력이 출력으로 3차원 벡터가 되었고, 행렬의 행이 각 출력에 계수가 되었지요?
$
\begin{equation*}
\begin{bmatrix}
w_{11} & w_{12} \\
w_{21} & w_{22} \\
w_{31} & w_{32} \\
\end{bmatrix}
\begin{bmatrix}
x_1 & x_3\\
x_2 & x_4\\
\end{bmatrix}
=\begin{bmatrix}
y_1 & y_4 \\
y_2 & y_5 \\
y_3 & y_6
\end{bmatrix}
=\begin{bmatrix}
w_{11}x_1 + w_{12}x_2 & w_{11}x_3 + w_{12}x_4 \\
w_{21}x_1 + w_{22}x_2 & w_{21}x_3 + w_{22}x_4\\
w_{31}x_1 + w_{32}x_2 & w_{31}x_3 + w_{32}x_4
\end{bmatrix}
\end{equation*}
$
자, 이것은 열 벡터 입력이 2개가 되었을 때 이지요? 그러면 열벡터 출력도 2개가 되겠군요. 잘 보면 행렬의 행이 각 출력의 계수가 된 채로 두 개의 2차원 입력 열 벡터를 2개의 3차원 출력 열 벡터로 만들었습니다. 그냥 그렇고 그런 시덥잖은 이야기입니다.
자, 여기까지 보았으니, 실생활에서 행렬이 어떻게 이용되는지도 한번 봐야 속이 시원해지겠습니다.
예를 들어, 우리가 햄버거와 콜라를 사려고 하는데요, 햄버거와 콜라는 각 3개와 2개를 사려고 합니다. A회사와 B회사에서 어디서 살까 고민하고 있습니다. 각 회사에 대한 총 구매 금액을 한 번에 계산하고 싶다고 한다면 다음과 같이 문제를 생각해 볼 수 있을 것 같습니다.
일단, 입력 벡터는 $(3, 2)^T$로 2차원 열 벡터라고 생각하고요, 이 개수를 전체 구매 금액으로 변환하려면 각각의 살 개수에 가격을 곱해서 더해주면 전체 금액으로 변환되겠습니다. 이때 출력 벡터는 A, B회사에 대한 전체 금액이니까, 2차원 열 벡터가 나오면 되겠군요. 그러면, 2차원 입력에 2차원 출력이니까, 2X2 행렬이 되겠습니다. 호.
오, 그렇다면 여기에서 한 단계만 더 나간다면, 살 개수를 바꿔서도 비교하고 싶다면, 입력 열벡터에 살 개수를 추가해서 계산하면 곧바로 계산이 가능하겠습니다.
아하! 변환시킬 수 있는 행렬은 이런 식으로 구현이 되겠군요. 간단하네요. 그러면 여기에서 행렬의 곱셈을 한단계 더 진화시켜 줄까요?
공룡 공장에서 오늘 아침에 휘발유와 경유 가격을 확인해 보니, 휘발유가 1통당 2000원, 경유가 1통당 1000원이었습니다. 이 공장에는 새 기계와 중고기계가 있고, 새기계와 중고기계는 휘발유와 경유를 넣고 운전하게 되는데, 이때 새기계와 중고기계에 들어가는 시간당 비용을 계산하고 싶다고 합시다.
그러면 입력 열 벡터는 $(2000, 1000)^T$이고요, 변환 행렬은 시간당 소요되는 휘발유와 경유의 개수를 각각 알면 변환 계산이 되겠군요.
아, 그런데 여기에서 끝이 아니고, 오전/오후로 나눠서 총 운전시간을 이용해서 오전/오후에 대한 총 소요 비용을 계산한다면, 시간당 소요되는 비용을 입력 벡터로 오전/오후에 대한 새 기계 중고기계의 운전시간을 알면 전체 소요 비용이 나오겠습니다.
이게 말로 하니까, 조금 어렵지만 결국 행렬 계산은 다음과 같이 할 수 있습니다.
어떤가요? 이렇게 하면 연속적인 행렬곱으로 변환을 계속해서 이어갈 수 있다는 흥미로운 결과를 알 수 있겠습니다.
그러면 조금만 더 익숙해 지기 위해서, 이런 예를 들어보겠습니다.
어느 학교에서 교사 12명과 학생 300명이 오전과 오후로 나누어 미술관을 관람하려고 합니다. 교사와 학생이 오전/오후를 선택한 결과와 관람료는 다음과 같습니다. 총관람료를 계산해 봅시다.
자, 제일 먼저 우리가 입력 벡터를 무엇으로 보면 좋을지 고민해 봅시다. 입력 벡터로는 결국 정상가격을 변환하면 좋겠군요. 정상가격을 입력벡터로 해서 오전 오후의 사람 수를 곱해 전체 비용을 구한 후에, 오전 오후의 할인율을 이용해서 변환하면 최종 전체 비용이 구해지겠습니다.
$$
\begin{equation*}
\begin{bmatrix}
0.9 & 0.95
\end{bmatrix}
\begin{bmatrix}
5 & 140\\
7 & 160\\
\end{bmatrix}
\begin{bmatrix}
5000 \\
3000 \\
\end{bmatrix}
\end{equation*}
$$
행렬이라는 거 매우 흥미롭죠. 어떤 벡터를 변환 행렬을 이용해서 변환시킬 수 있다. 그것이 전부입니다. 여기에서부터 모든 선형대수의 것들이 파생되게 되는 것입니다. 그래서 변환이라는 측면에서 쉬운 변환 행렬들이 무엇이 있는지를 살펴보면
확대(축소), 회전, 한축만 늘리기, 없애기, 3D를 2D로 축소 회전등의 행렬들이 유명한 변환 행렬입니다. 차례로 늘어놓아 보면 이런 것들입니다.
$
\begin{equation*}
\begin{bmatrix}
a & 0 \\
0 & b
\end{bmatrix},
\begin{bmatrix}
cos\theta & -sin\theta \\
sin\theta & cos\theta
\end{bmatrix},
\begin{bmatrix}
a & 0 \\
0 & 1
\end{bmatrix},
\begin{bmatrix}
0 & 0\\
0 & 0\\
\end{bmatrix},
\begin{bmatrix}
cos\theta & -sin\theta & 0 \\
sin\theta & cos\theta & 0 \\
0 & 0 & 1
\end{bmatrix}
\end{equation*}
$
이제까지 이야기를 보면 행 벡터를 변환, 열 벡터를 변환순서로 살펴보았는데, 수학적으로는 열벡터 입력에 열 벡터로 변환 표현이 매우 많습니다.
우리가 다루는 데이터를 보면 각 행(row)이 하나의 벡터를 구성하는 경우가 많은데요. 열(column)은 Feature를 나타내고요. - n개의 Feature는 n차원으로 대치할 수 있겠네요 -
이런 데이터의 한 행을 열 벡터로 만들어서 행렬로 다루는 일이 많은데요, 이런 표 형태의 행을 열벡터로 바꿀 때, Transpose를 써서 다룹니다.
그렇게 되면, W를 변환 행렬, X를 입력 열 벡터로 다룰 수 있게 되어
$$ WX^T $$
의 형태로 표현할 수 있습니다.
이런 데이터를 행렬로 표현하려다 보니, 뭔가 여러 가지 응용문제들이 등장하게 되는데요,
1) 출력 벡터와 입력 벡터를 알고 있다면, 이렇게 만드는 변환 행렬의 원소 값을 추정하는 문제가 있을 수 있는데, 이런 문제가 선형 임베딩, 선형 회귀, 로지스틱 회귀, 딥러닝 등의 응용문제가 있을 수 있고,
2) 데이터를 대칭 행렬로 만들어서 데이터를 분석하는 방법이 있을 수가 있는데, 이런 것들이 주성분 분석, 잠재 의미 분석 등의 응용이 있을 수 있겠습니다.
이외에도 많은 응용들이 있을 수가 있겠습니다.
현상을 행렬로 모델링하려고 보니, 여러 가지 필요한 것들이 나타나게 되는데, Eigen Vector, Inverse 등이 있어야 우리가 일반적으로 다루는 방정식 같은 느낌으로 행렬을 다룰 수 있게 됩니다. 그런 것은 선형대수의 본격적인 내용이 되니. 그런 건 필요할 때마다 둘러보면 좋겠습니다. 휴.
친절한 데이터 사이언스 강좌 글 전체 목차 (링크) - 
댓글