일단 비율이라는 말이 나오면 곧바로 떠올려야 하는 것이 (중심극한정리에 의한) 큰 표본 Binomial의 Gaussian 근사를 떠올려야 합니다. 이미 이전에 자세히 살펴보았으니, 조금은 다시 만나 반갑다는 제법 의연한 마음가짐을 가졌으면 좋겠습니다.
비율을 검정할 때는 $np\ge5, nq\ge5$인 경우의 Gaussian 근사를 활용한 z 검정이구나!라고 떠올리면 됩니다. 왜냐하면 비율을 비교할 때 아주 작은 수의 표본을 보는 경우는 하지 말아야 하지 않을까요? 적당히 큰 표본일 때 비율을 따지는 것이 정상인의 행동 범위라고 생각합니다.
우선 Binomial은 $X_{n,p} \sim B(n,p) \sim N(np, npq)$이고요, 비율에 관한 것들은 모두 여기에서부터 시작한다고 생각하면 틀림없습니다.
이미 살펴보았지만 다시 한번 전개한다면, $X_{n,p}$가 성공 횟수이니까, 이것을 이용해 전체 시행 횟수와의 비율로 나타내어, Gaussian으로 근사한다면,
$$\cfrac{X_{n,p}}{n} = p \sim N\left(p, \cfrac{pq}{n}\right) \\ \because E\left(\cfrac{X_{n,p}}{n}\right)=\cfrac{np}{n} = p, \,\,\,\,\,\,\,Var\left(\cfrac{X_{n,p}}{n}\right) = \cfrac{npq}{n^2} = \cfrac{pq}{n}$$
입니다.
이것만 알면 비율에 관한 한 뭐든지 만사형통입니다. 그렇긴 한데, 이 시점에서 비율에 관련된 통계적 접근은 3가지가 있는데, 이 세 가지에서 분산을 구하는 방법이 조금씩 다릅니다. 논리가 달라서 그런데, 원리는 아주 간단합니다. 구분해서 이야기해 보자면 다음과 같습니다.
⓵ 모비율에 대한 신뢰구간 구하기
⓶ 모비율에 대한 검정
⓷ 두 집단의 비율의 차이 검정
일단, 결론부터 이야기하자면 ⓵⓷ 의 경우와 ⓶의 경우가 분산이 다릅니다.
⓵의 경우에는 표본을 통해서 모비율의 신뢰구간을 추정하는 것이기 때문에 표본의 비율이 분산으로 사용됩니다. $\cfrac{\hat{p}\hat{q}}{n}$죠. 모비율을 모르니까요. 그러니까 모비율을 추정하는 것이겠죠.
⓶의 경우에는 Null Hypothesis가 맞다는 가정으로 표본이 어떻게 관측되었는지 접근하기 때문에 검정하고자 하는 비율(모비율)이 정해지고 그에 대한 분산이 계산되어집니다. $\cfrac{{p}{q}}{n}$죠. 모비율을 특정값으로 가정합니다. 그때의 검정통계량은 $Z = \cfrac{\bar{X}-\mu}{\sigma}$와 똑같은 원리로 본다면, $Z = \cfrac{\hat{p}-p}{\sqrt{\frac{{p}{q}}{n}}}$ 이겠습니다. 1표본 t검정에서는 표본분산을 이용했는데, 1표본 비율검정에서는 가정된 모집단의 비율 p에 의한 모분산$\sqrt{\dfrac{pq}{n}}$을 곧바로 계산할 수 있다는 점입니다. 그닥 다른 이야기가 아닙니다.
⓷의 경우에는 표본을 통해서 두 집단의 비율 차이를 확률적으로 계산하려는 것이기 때문에 표본의 비율이 분산으로 사용됩니다. $\cfrac{\hat{p}\hat{q}}{n}$죠. 두 집단의 모비율을 모르니까 어쩔 수 없습니다.
다시 한번 정리하면
⓵ 모비율에 대한 신뢰구간 구하기 : 모비율 값을 특정하지 못함 → 분산은 $\hat{p}$를 이용함
⓶ 모비율에 대한 검정 : 모비율을 그렇다 치고~ 값을 정할 수 있음 → 분산에 p를 이용함
⓷ 두 집단의 비율의 차이 검정 : 각각의 모비율 값을 특정하지 못함 → 분산에 $\hat{p}$를 이용함
조금 복잡한 것 같지만, 모비율을 특정값으로 특정할 수 있는가 없는가에 따라서 구분이 된다는 것만 이해하면 그다지 어려울 것이 없는 이야기입니다. 일단, ⓵번의 신뢰구간의 추정은 이미 살펴보았으니, ⓶번과 ⓷번의 검정에 대해 살펴보고 직접 검정을 해보는 것이 신상에 이롭겠습니다.
먼저 ⓶ 모비율에 대한 검정을 다시 한번 정리하면, 모비율을 p라 치고, 어떤 비율을 관측했을 때, 과연 그 모비율이 맞을지 검정할 수가 있습니다. 그때의 검정 통계량은 $Z_{stat} = \cfrac{\hat{p}-p}{\sqrt{\frac{{p}{q}}{n}}}$ 입니다. 이것을 이용해서 검정을 하게 되고요,
⓷ 모비율 차이에 대한 검정은 모비율의 차이를 0으로 한 Null Hypothesis를 설정하고 검정하게 되는데, Independent Samples t test에서 했던 평균의 차가 0 인 조건의 분포와 똑같이 취급할 수 있습니다. 당연히 그런 게 있었지 정도는 기억하실 수 있다고 생각합니다.
$$
T=\frac{(\bar{X}-\bar{Y})-\left(\mu_{X}-\mu_{Y}\right)}{\sqrt{\left(\frac{s_X ^2}{n_{X}}+\frac{s_Y ^2}{n_{Y}}\right)}} \sim \mathcal{N}(0,1)
$$
요거를 비율로 대치하면 (표본의 비율로 근사해서, 모자를 쓴 hat은 관측값입니다.)
$$
Z=\frac{(\hat{p_X}-\hat{p_Y})-\left(p_{X}-p_{Y}\right)}{\sqrt{\left(\frac{\hat{p_X}\hat{q_X} }{n_{X}}+\frac{\hat{p_Y}{\hat{q_Y}}}{n_{Y}}\right)}} \sim \mathcal{N}(0,1)
$$
가 됩니다. 여기에서 한 단계 더 나아가 합동비율로 더 간략화하긴 하지만 그 이야기까지는 조금만 이따가 하도록 합시다. 요컨대 비율에 관해서는 평균과 분산을 대치하면 끝납니다. 이게 끝입니다. 평균 비교와 똑같으니까요. 그냥 끝난 거예요.
정리가 끝났는데 말이죠, 너무 짧게 끝나면 너무 없어 보이니까, 예를 들어서 한번 검정을 해보죠. 그러니까 한 번에 모비율의 검정, 모비율차에 대한 검정을 한큐에 다뤄볼까 합니다. 애매하게 길지도 짧지도 않은 이야기가 되겠군요.
먼저 모비율을 불쑥 검정!
사연 : 악어를 키우는 앱이 있는데, 푸시를 통해 새롭고 귀엽고 매력 터지는 악어에 대한 캠페인의 응답률이 국가별 평균과 다른지 여부를 확인하려고 하는데, 푸시를 받은 1000명의 유저중에서 87명이 광고를 받은 후 새롭고 귀엽고 매력터지는 악어를 구매했습니다. 새롭고 귀여운 악어를 구입한 유저의 비율이 국가별 평균 6.5%와 다른지 확인하고 싶습니다.
자, 이런 경우라면 6.5%와 새로 관측한 87/1000이 95%신뢰구간(5% 유의확률) 내에 있는지를 보는 이야기이겠군요. 가설을 세우자면 p=6.5%라고 치고~라는 것으로 척척척하면 되겠습니다.
Null Hypothesis는 p=6.5%이고,
Alternative Hypothesis는 ≠ 6.5%이겠습니다.
그러니까 양측검정이겠군요.
그러면 Null Hypothesis에 의한 p의 분포는 평균 p, 분산 $\cfrac{pq}{n}$인 Gaussian이니까 이를 이용해서 검정할 수 있겠습니다. 그러면 우리가 관측한 1000명 중 87명이 구매한 현상을 보고 기존의 6.5%와 다른지 확인해 봅시다. 즉, 0.087을 목격한 것이죠.
일단 관측치에 따른 표준화된 검정통계량은 $Z_{stat} = \cfrac{\hat{p}-p}{\sqrt{\frac{pq}{n}}} =\cfrac{87/1000-0.065}{\sqrt{\frac{0.065(1-0.065)}{1000}}}=2.82$ 입니다.
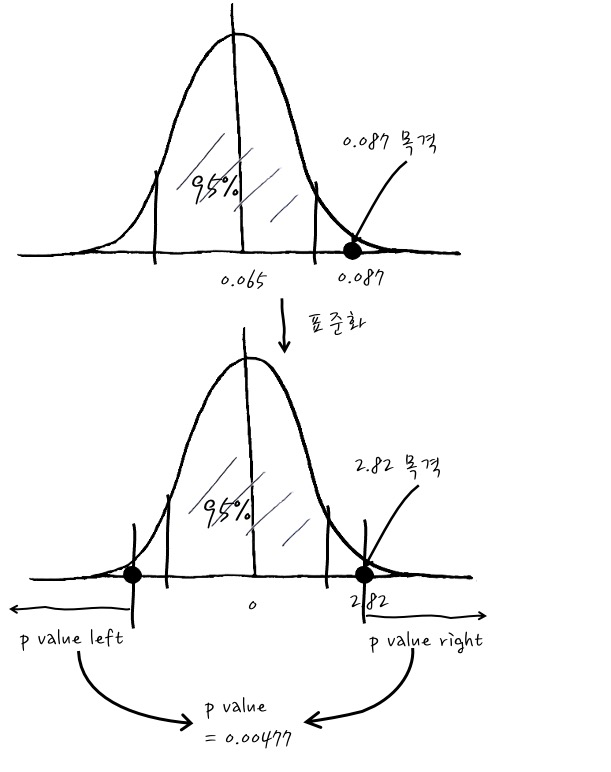
이걸 계산해 보면 관측치가 신뢰구간 2.5%의 바깥쪽에 있고, p value가 0.477%로써 유의확률보다 많이 작군요. 그러니까, Null Hypothesis를 기각할 만한 증거를 발견! 했다고 결론을 맺으면 정확한 이야기입니다. 그러니까 결국 차이가 나는군요!라는 결론입니다.
후후 별거 아니군요.
이걸 statsmodel 패키지의 proportions_ztest를 이용해서 구하는 과정을 한번 해본 다면,
import scipy
from statsmodels.stats.proportion import proportions_ztest
import math
p = 0.065
q = 1-p
n = 1000
nobs = 87 # Number of OBservationS
p_hat = nobs/n
q_hat = 1-p_hat
z_stat = ((p_hat-p)/(math.sqrt(p*q/n)))
pstat, ppval = proportions_ztest(nobs, n, p, "two-sided", prop_var=p)
print("z_stat : %f"%(z_stat))
print("p value two-sided : %f" %((1-scipy.stats.norm(0, 1).cdf(z_stat))*2))
print("z_stat statsmodel : %f"%(pstat))
print("p value two-sided statsmodel : %f"%(ppval))
z_stat : 2.822021
p value two-sided : 0.004772
z_stat statsmodel : 2.822021
p value sstatsmodel : 0.004772
z_stat, p value two-sided는 통계량과 p value를 직접 계산한 결과이고, pstat, ppval은 statsmodel의 패키지의 검정을 이용한 것입니다. 결과가 똑같습니다. 호오-
검정 원리만 안다면, 통계 소프트웨어의 도움을 받으면 의자에 턱 앉아 머리를 텅 비워놓은 채로 제 편에서 멋대로 쓱쓱 앞으로 나아가 주니 무척 편합니다.
그러면, 이번엔 모비율 차이에 대한 검정을 볼까요? 모비율 차이 검정을 가장 잘 쓸 수 있는 예시가 바로 A/B 테스트입니다. 이거야 말로 통계를 활용한 간단한 분석의 꽃이죠. 이미 이전에 신뢰구간을 활용한 A/B테스트를 한번 본 적이 있습니다. 그때는 비율이 아니라 평균의 비교라서 평균의 신뢰구간이 서로 겹치는 지를 간단하게 확인했지만, 이번에는 평균이 아니라 비율입니다. 사연을 들어볼까요?
사연 : 코끼리 밥 주기 앱을 서비스하는 우리 회사는 이번에 하는 앱 설치 마케팅 캠페인의 효과를 A/B테스트를 통해 측정하려고 합니다. 새로운 캠페인 중 A 안은 50명이 랜딩페이지에 왔다가 20명이 앱을 설치했고, B 안은 추적을 해 보니, 200명이 랜딩페이지에 도착 후 120명이 앱을 설치했습니다. 자, 이런 경우에 B 캠페인이 앱 설치도가 더 좋다는 주장을 지지하는지 한번 보시죠! - 사실 이거는 너무 차이가 커서 굳이 검정할 필요가 있을까 싶지만 실제로 B안이 A안보다 효과가 있었는지에 대한 분석은 어떻게 하는지 보겠습니다. -
$$Z=\frac{(\hat{p_B}-\hat{p_A})-\left(p_{B}-p_{A}\right)}{\sqrt{\left(\frac{\hat{p_B}\hat{q_B} }{n_{B}}+\frac{\hat{p_A}\hat{q_A}}{n_{A}}\right)}} \sim \mathcal{N}(0,1)
$$
이때 분산이 표본의 분산으로 계산된다는 점은 주의해 주세요. 관측치 $\hat{p}$를 이용해서 분산을 계산합니다. 모분산을 특정할 수가 없으니까요. 이게 정석이긴 한데, 이것을 또 한 번 Simplify 하는 경우가 있습니다. 어떤 식이냐면 $\hat{p_A}, \hat{p_B} \sim \hat{p_0}$ 형태로 공통표본비율(합동표본비율)로 한번에 퉁쳐서 Simplify하는 경우인데요, 이 경우는 $p_0 = \cfrac{count_A+count_B}{n_A+n_B}$로 전체 발생건수/ 전체 표본수로 간략화해서 계산하기도 합니다. 그닥 크게 차이 나진 않지만 시험용으로 공부한다던지, statsmodel proportions_ztest는 이런 Simplify 버전을 계산을 하기 때문에 알고 있으면 편리하겠습니다. 물론 정식으로 계산한 값과 조금 차이가 날 수 있습니다. 그러니까 결국
$$Z=\frac{(\hat{p_B}-\hat{p_A})-\left(p_{B}-p_{A}\right)}{\sqrt{\hat{p_0}\hat{q_0} \left(\frac{1 }{n_{A}}+\frac{1}{n_{B}}\right)}} \sim \mathcal{N}(0,1)$$
이런 식의 간략 버전이 있습니다. 이 간략 버전과 원래 버전 무엇이 맞는가를 고민할 필요가 전혀 없습니다. 뭐 그런 게 있었는데? 정도만 기억하면 어떨까 합니다.
이제는 기계적으로 가설을 세우고 검정에 돌입해 보겠습니다.
각각의 A안과 B안에 대하여, $\hat{p_A}=20/50=0.4, n_A=50, \hat{p_B}=120/200=0.6, n_B=200$ 입니다. 0.4와 0.6의 대결이군요.
Null Hypothesis는 $p_B - p_A \le 0$이고,
Alternative Hypothesis는 $p_B - p_A > 0$으로 가설을 설정하면, Null Hypothesis로 분포를 결정할 수 있고, Alternative Hypothesis로 새로운 캠페인이 효과적이었다는 주장을 포함할 수 있겠군요.
그때의 Null Hypotheis가 참일 때의 검정통계량은 $p_B-p_A=0$로 설정한 분포에서의 관측값이고, 공통 비율$p_0 = \cfrac{20+120}{50+200}=0.56$입니다. 공통표준편차는 $\sqrt{0.56\times(1-0.56)\left(\frac{1}{50}+\frac{1}{200} \right)}=0.0784\cdots$ 입니다.
$Z_{stat} = \cfrac{0.6-0.4}{0.0784\cdots} = 2.54\cdots $ 가 되겠습니다.
이걸 statsmodels를 이용해서 검정을 해 보겠습니다.
from statsmodels.stats.proportion import proportions_ztest
import numpy as np
# 이거는 직접 계산
count_b = 120
count_a = 20
n_b = 200
n_a = 50
p_a = count_a/n_a
p_b = count_b/n_b
p_0 = (count_b+count_a)/(n_b+n_a)
prop_var = math.sqrt((p_0*(1-p_0)/n_a + p_0*(1-p_0)/n_b))
z_val = (0.6-0.4)/prop_var
print("z_stat : %f"%(z_val)) # 직접 계산
print ("p_val : %f"%(1-scipy.stats.norm(0, 1).cdf(z_val))) # 직접 계산
# 이거는 statsmodel 이용해서 검정
count = np.array([count_b, count_a])
nobs = np.array([n_b, n_a])
stat, pval = proportions_ztest(count, nobs, alternative="larger")
print("z_stat statsmodels : %f" %(stat)) # 라이브러리 이용
print("p_val statsmodels : %f " %(pval)) # 라이브러리 이용
> 직접 계산값
z_stat : 2.548236
p_val : 0.005413
> statsmodel 결과값
z_stat statsmodels : 2.548236
p_val statsmodels : 0.005413
결과를 보시면 직접 계산한 것과 statsmodels를 이용한 것이 같은 결과를 내지요? 호오. 자, p value를 보면 0.05보다 훨~씬 작군요. 그러니까 5% 유의수준 (95% 신뢰수준)으로 두 비율(B-A)의 차이가 0보다 작거나 같다라는 Null Hypothesis가정 아래 B안이 아주 큰 증거를 발견했으므로 귀무가설 기각! 그러니까 B안이 전환율이 더 좋다. 고 말할 수 있겠습니다. 뭐 이런 스토리입니다.

그런데, proportions_ztest()를 이용할 때 꼭 알아야 할 것이 있습니다. proportions_ztest(관측횟수, 표본크기, 모비율, 대립가설, 귀무가설의 분포 계산을 위한 비율) 을 설정할 수 있게 되어 있는데, 이 중에서 모비율의 검정을 할 때 귀무가설의 분포 계산을 위한 비율을 아무것도 안 주면 (또는 False) 주어진 표본을 이용하여 계산해 버려서 통계량이 생각한 것과 다르게 나옵니다. 처음에 다룰 때 당황하지 않으면 좋겠습니다.
 친절한 데이터 사이언스 강좌 글 전체 목차 (정주행 링크) -
친절한 데이터 사이언스 강좌 글 전체 목차 (정주행 링크) - 

댓글