설마 범주형 독립변수도 회귀가 가능한가요? - Dummy Variable

이제까지는 연속형 독립변수를 이용해서 회귀를 했었잖아요? 회귀 분석을 할 때 늘 연속형 독립변수만 있는 것은 아니잖아요? 예를 들면 남/여, 학년, 혈액형, MBTI 뭐 이런 것들이거든요. 이런 변수는 숫자로 나타나 있는 값이 아니니까 회귀분석에 사용하기 애매합니다. - 아니 이런 것도 회귀를 한다니.. 적당히라는 것을 모르나 봅니다... -

자, 이럴 때 범주형 변수를 숫자형 변수로 만들어서 회귀를 할 수 있습니다. 어떤 식이냐면 데이터의 범주를 1, 0으로 Feature를 늘려서 보는 것입니다. 이게 먼 소리인가 하면, 예를 들어 다음과 같은 데이터가 있다고 해 보시죠. 한번 자세히 쓱 봐주세요.

 

이 데이터에는 성별과 혈액형이 범주형 데이터입니다. 이해하기 편하게 일단 성별 Feature를 Dummy Variable로 만들어 보시죠. 어떤 식이냐면  남/녀 이렇게 2가지 성별이 있겠죠. 2가지 성별을 1과 0으로 잘 표현하는 방법이라는 게 별게 있겠습니꽈. 이런 겁니다. 

'

 

이런 식으로 성별이 남자인 경우에는 성별_남자만을  1로 나머지는 0, 여자인 경우에는 성별_여자만 1로 나머지는 0으로. 이런 식으로 표현할 수 있겠습니다. 이런 식으로 숫자로 나타낼 수 있으니까, 결국 회귀분석을 할 수 있겠습니다. - 참고로 이렇게 범주형 변수를 1/0 형식으로 만들어 주는 행위를 One Hot Encoding이라고 합니다 - 이런 One Hot Encoding 한 변수를 Dummy 변수라고 합니다. 

그런데, 여기에서 조금 조심해야 할 부분이 있겠는데, 이렇게 모든 범주를 고려해서 Dummy 변수를 만들어주게 되면 어떤 문제가 생기느냐 하면 또 그놈의 완벽한 다중공선성이라는 것이 발생합니다. 이게 무슨 말이냐면 

예를 들어, 성별_남자, 성별_여자를 모두 감안해서 회귀를 하게 되면 
$$ y = b_0 + b_{1}x_{man} + b_{2}x_{woman} $$ 

이런 회귀식을 구하게 될 텐데, 남자와 여자의 관계는

$$x_{man} + x_{woman} = 1$$ 의 관계를 갖습니다.

그러니까, 
$$ x_{woman} = 1 - x_{man}$$
이런 식의 관계식이 성립합니다. 

흠. 자, 그럼 원래 회귀식에 이걸 넣어보면

$$\begin{aligned} 
y &= b_0 + b_{1}x_{man} + b_{2}x_{woman} \\&= b_{0} + b_1(1-x_{woman}) + b_2 x_{woman} \\&= (b_0 + b_1) + (b_2-b_1)x_{woman} 
\end{aligned}$$ 

이렇게 정리되겠습니다. 이렇게 되면 성별 중 여자 하나로 회귀식이 풀리게 되고, 원래 분석하려던 계수들이 섞여 버려서 나누어 분석할 수 없게 엉망이 되어 버릴뿐더러, 혹시라도 행렬을 이용하여 회귀를 풀게 되면 Determinant가 0이 되어버립니다. 이거 보면 엇? 다중공선성 그거 맞죠? 우리가 원래 설명하려던 계수들 설명을 못하게 되는 현상. 바로 전까지 이거 때문에 엄청 고민했었는데 여기서 또 속을 썩이네요. 털썩.

$$ x_{woman} = 1 - x_{man}$$

이런 식으로 독립변수가 서로 선형관계를 맺게 되면 안 된다는 거요. 으흠~ - 이렇게 Dummy Variable이 다중공선성을 띄여서 문제가 발생하는 것을 유식한 말로 Dummy Trap이라고 합니다. -

그러면 어떻게 해요? 

 

이런 식으로 여자냐 아니냐 1개로 구분해서 하면 딱 좋습니다. 0이면 당연히 여자가 아니다. 그러니까 남자를 뜻하겠죠. 이러면 Dummy 변수로 인한 다중공선성 따위는 잊어버려도 되니까요. 말 그대로 성별이 0일 때는 남자, 1일 때는 여자로 해석하면 됩니다. 
그렇다면 혈액형은 4가지 종류나 되는데 이건 어떻게 하면 좋을까요? 

 

이때도 마찬가지로 혈액형 A일 때를 제외하고 만들면 됩니다. 모두 0일 때는 A이니까요. (A형이 해석의 기준이 되겠습니다)

그런데, 다중공선성 운운하면서 다중공선성을 고려해서 Dummy 변수를 만들어야 한다고 이야기 하긴 했는데,  그렇다면 A형 1, B형 2, O형 3, AB형 4 이런 식으로 정하면 되지 않나요? 하는 의문이 생길 수가 있을 텐데, 이렇게 정하게 되면 값에 대해서 크기에 따라 순서가 생기게 되고, 순서가 생기게 되면 회귀를 할 때 이 크기가 의미를 갖게 됩니다. 범주라는 것은 그런 의미가 아니니까, 모두 따로따로 만들어서 그런 순서가 생기지 않도록 만듭니다. 후후.

결국에 Dummy 변수라는 건 모든 값이 0인 경우를 기준으로 하면 다른 범주들과 기준범주를 비교할 수 있겠습니다. 
자, 이제 범주형 데이터를 Dummy Variable로 만드는 방법에 대하여 알았으니까 해석방법을 통해 의미도 알아야 하겠죠.

가장 중요한 점은 Dummy는 범주형 데이터이기 때문에 회귀식의 기울기에는 관여하지 않고, y절편에 관계합니다. 

어떻게 그러냐고요? 

 

이럴 때, x₁이 Dummy인 경우라고 생각해 보면 x₁이 1이면 x₁의 계수 b₁만큼, x₁이 0이라면 x₁의 영향력이 없어지므로 x₁이 0일 때와 1일 때의 차이만큼 Shift가 되기만 하고 기울기에는 영향이 없습니다. 지금은 1개의 Dummy변수에 관련하여 보았는데, 이게 혈액형의 경우처럼 여러 개라면 그 개수만큼 y절편의 Shifting 생길 것입니다. 매우 간단간단합니다. 그러니까 x₁을 성별이라고 생각한다면 남성과 여성이 b₁만큼 차이가 난다고 해석하면 되는 겁니다. 후후.

결국 기준 더미 변수로부터 0이 아닌 Dummy의 계수만큼 차이가 난다는 의미로 해석을 하면 되겠습니다. 

그러면, 이 Dummy 변수라는 것을 알게 되었으니까, Dummy 변수가 포함된 회귀를 한 후에 그 결과를 해석할 수 있어야 하겠습니다. 회귀분석은 많이 해봤으니까 건너뛰고요, 결과 해석만 해 보도록 하겠습니다. 예시 분석 결과를 보고 해석 고고.

 

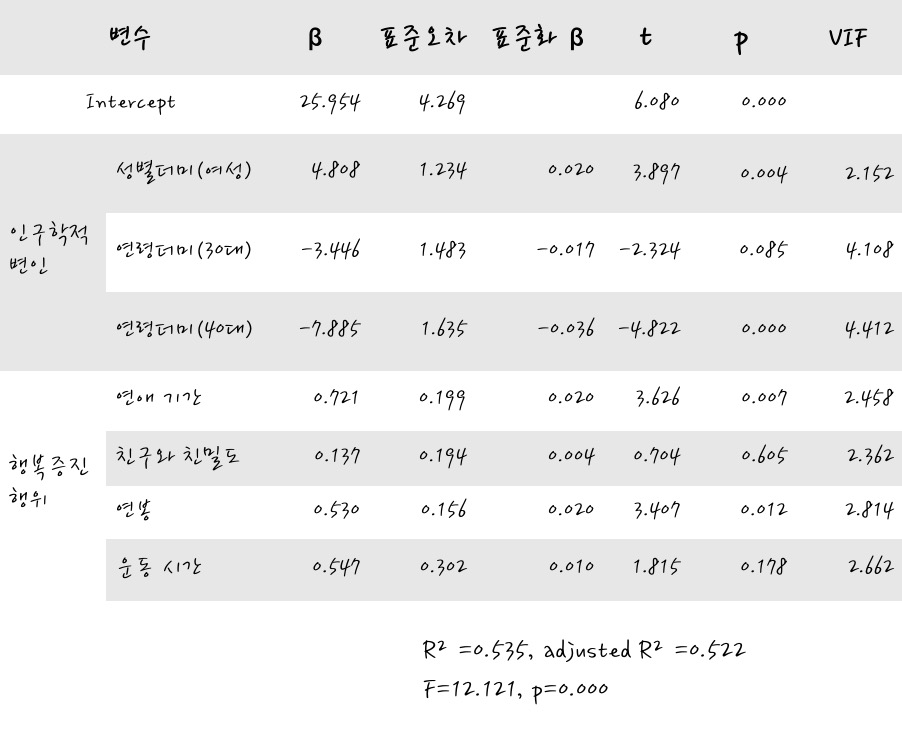
이 결과는 종속변수가 자신의 행복도, 연령 Dummy에서 기준 Dummy변수는 20대인 회귀분석의 결과입니다. 

회귀식으로 이야기한다면,

$$\begin{aligned} y_{happy} = b_0 &+ b_1 x_{woman} + b_2 x_{age30} + b_3 x_{age40} \\ &+ b_4 x_{dating} + b_5 x_{friendship} + b_6 x_{salary} + b_7 x_{excercise} \end{aligned}$$

이런 회귀식으로 이해하면 좋겠습니다. 자, 회귀 결과 분석표를 보면서 차근차근 해석해 보시죠.  

⓵ 결정계수와 수정 결정계수를 를 보니 꽤 높군요? 0.535, 0.522. 회귀식 설명력이 꽤 높습니다. 

⓶ F검정 결과가 유의합니다. F통계량이 12.121로 꽤 큽니다. 확률적으로 의미 있는 회귀 분석 결과라고 생각합니다. 

⓷ VIF를 보니 문제가 될 만큼 큰 크기의 변수가 보이질 않네요. 정말 다행입니다. 모형에는 다중공선성이 발견되지는 않았습니다. 그렇지만 참고로 Dummy 변수의 VIF가 큰 경우에도 Dummy 변수가 우리가 꼭 분석해야 하는 범주형 변수라면 그대로 두고 해석해야 합니다. 

⓸ 계수의 유의성을 참고해서 해석해 보면, 더미(독립)변수는 여성, 30대 연령이 유의했고, 나머지 독립변수 중 유의한 것들은 연애기간, 연봉입니다. 그렇다는 이야기는, 여성과 남성의 행복도의 차이가 나고요,  20대(기준)와 40대의 행복도가 차이가 납니다. 30대의 경우에는 계수가 유의하지 않아 기준연령인 20대와 차이가 난다는 증거를 발견하지 못했다고 생각하면 됩니다. 그리고 연애기간, 연봉에 따라 얼마나 행복도에 영향을 끼치는지 자신감을 가지고 이야기할 수 있습니다. 

⓹ 그러면 이 분석결과를 영향력을 보려면 표준화된 계수와 함께 보면 상대적인 영향력을 잘 설명할 수 있겠습니다. 40대가 -0.036으로 부정적으로 큰 영향을 주었으며, 다음으로 여자 인가 와 연애기간이 0.02, 연봉이 0.02의 순으로 영향을 미칩니다. 종합해서 해석하면 여자이고, 연애기간과 연봉이 클수록 행복도가 높아지고, 나이로 본다면 40대라는 나이는 20대에 비해 행복감에 부정적인 영향을 준다고 해석할 수 있겠습니다. 

⓺ 구체적으로 실제값의 변화를 해석해 보면, 여성이 남성에 비해 4.808 정도 더 행복했고, 20대에 비해 40대가 7.885 정도 덜 행복합니다. 연애기간은 1 단위 (1년) 늘때마다 0.721 행복해 졌고, 연봉은 1단위 (100만원)이 늘 때 마다 0.530 만큼 더 행복해졌습니다. 

분석 결과가 정말 현실적이군요. 연봉이 클수록 행복도가 높아지고, 

어떤가요? 별거 아니죠? 헤헤.

참고로 pandas Dataframe에는 이런 Dummy Variable을 자동으로 만들 수 있는 방법이 제공되는데, 그게 pd.get_dummies(data=df, columns=['성별', '혈액형'] 이런 식으로 해 주면 자동으로 컬럼을 분석해서 Dummy를 만들어 줍니다. 이때 drop_first=True를 추가해서 넣어주면 아예 첫번째 값을 0으로 해서 전체범주-1 개의 Dummy 컬럼을 만들어주긴 하는데, 이게 first의 reference값이 무엇인지를 사용자 마음대로 지정할 수가 없는 불편함이 있긴 합니다. 그래서 그냥 first drop을 하지 않고, dummy를 만든 후에 reference 컬럼을 drop 해 버리는 방식을 사용합니다. 후후.

지금까지 독립변수가 범주형과 양적변수를 경우를 따져봤는데, 반대로 종속변수가 범주형 Dummy변수라면 어떻게 될지도 궁금해지는군요. 예를 들어 어떤 사람이 결혼을 할지(1) 안 할지(0)에 대한 의사결정을 하려고 한다면. 이러한 의사결정은 임금, 교육 수준, 상대방 외모와  같은 여러 양적변수로 부터 영향을 받을 것인데, 이걸 그냥 OLS회귀분석을 해 버리면 여러 가지 문제가 있을 수가 있습니다. 이런 경우에는 지금까지와는 다르게 로지스틱회귀(Logistic Regression)라는 걸 하는데, 분류하고도 연결이 됩니다. 흥미진진한 - 흠 - 다음 이야기 예고편이었습니다.