지금까지 계속 뭔가 수학적으로 최대/최소값에 목 매고 있는 것 아닌가?하는 생각이 들었다면 정확하게 짚었습니다. Cost 최소화 때문이라도 매우 중요한 이야기가 되는데, 어쨌든 그런 걸 구하다 보면 최대 최소값을 구하는 데 있어서 어떤 제약 사항이 있는 경우가 당연히 있지 않겠습니꽈.
보통은 어떤 제약사항에 대하여 최대 최소값을 구하는 방법이라는 게 제약사항과 관심함수의 접선과 접점을 구하면 간단하게 최대 최소값을 구할 수 있잖아요?
예를 들면,
$x^2+y^2=1$의 조건 하에서 $f(x,y) = x+y$의 최대. 최소값을 구하려고 한다면, 보통은 원을 그려놓고, x+y=c는 y=-x+c 를 계속 움직여서 접점 두개를 찾은 후에 그때의 c값의 최대값, 최소값을 구하게 될 텐데요. 이렇게 저렇게 두비둡둡룰루랄라 접선의 방정식을 구하면 $y=-x \pm \sqrt{2}$ 가 됩니다. 생각은 쉬운데, 이런 쉬운 경우에도 막상 계산해 보면 상당히 복잡합니다.

음. 이걸 다른 방식으로 바라보게 되면 조금 더 쉬운 방법이 있다는 건데요, 그게 바로 라그랑주/라그링지/라그랑쥬/라그랑쥐 승수법이라는 겁니다. 이게 좀 이름에 대한 발음이 여러 가지이기도 하고, 이 개념이 쉬운 듯 하지만 한방에 이해하기 좀 어려운데 어쨌든 중요한 파트는 승수법입니다. 이 방법이 앞뒤 없이 유용한 것이 3차원 이상의 차원이 되면 접선을 구해서 최대, 최소값 계산하기가 정말 만만치가 않습니다. 여튼 매우 유용하니까, 알아두면 최대 최소값 구할 때 어딘가에는 잘 써먹을 것이고, 아는 척하기에도 참 좋습니다. 라그랑(주,지,쥬,쥐)는 사람이름이니까 제대로 발음해야 하겠습니다만, 걍 가장 많이 알려진 라그랑주 승수법이라고 표기하겠습니다. 라그랑(주,지,쥬,쥐)님 이해해 주세요.
라그랑주 승수법에 대해서, 설명을 보다 보면 이게 왜 알듯 알듯 모르게 되는 거냐면, 구하려는 함수와 제약 함수의 접점에서 구하려는 함수와 제약 함수의 Gradient가 평행하다?로 설명을 설렁설렁한 후에 뭐, 그렇죠? 라면서 간단한 듯이 설명하다 보니 왜 그렇게 되죠? 라며 머리를 긁적이게 되는데, 이제부터 그것이 왜 그런지 이야기를 늘어놓도록 하겠습니다.
여기에서 중요한 점은 최대 최소를 구하기 위해서 접선 또는 접평면을 구하면 최대 최소값을 구할 수 있다는 사실은 변하지 않습니다. 이번에는 처음 시도하는 구분법인데 좀 있어 보이게 STEP을 3단계로 나눠서 차근차근 들여다보도록 하겠습니다.
STEP 1! 우선은 Gradient가 무엇인지를 알아야 하겠군요.
일단, Gradient의 정의가 뭔지 알고는 시작해야 하니까, 일단 정의를 적어는 놓고 그 의미를 살펴보도록 하겠습니다. Gradient는 역삼각형∇으로 표시하고 델타라고 읽습니다. 기호의 원래 이름은 나블라입니다. 다변수 함수에서의 정의는,
$$\nabla f = \left(\cfrac{\partial f}{\partial x_1},\cfrac{\partial f}{\partial x_2},\cfrac{\partial f}{\partial x_3}\cdots\cfrac{\partial f}{\partial x_n}\right)$$
이고요, 예를 들어 f가 x, y, z의 3 변수 함수라면,
$$\nabla f(x,y,z) = \cfrac{\partial f}{\partial x}i + \cfrac{\partial f}{\partial y}j + \cfrac{\partial f}{\partial z}k = \biggl \langle \cfrac{\partial f}{\partial x}, \cfrac{\partial f}{\partial y}, \cfrac{\partial f}{\partial z }\biggr \rangle$$
가 되겠군요. 각 변수 성분에 대한 편미분 벡터가 나옵니다. 벡터에 대해서 여러 가지 표현법이 있어서 여러가지 표현해 봤는데, 알면 신상에 좋습니다.
어쨌든 이게 어떤 다변수 함수를 Gradient를 하게 되면 다변수의 평면에 벡터가 나옵니다. 이 벡터가 나온다는 점에 주목해 주시고요. Gradient를 하면 미분도 하고 그러니까, 접선과 그것의 기울기가 생각나지 않겠어요? 게다가 많은 설명들이 가장 급한 쪽을 가리키는 벡터라는 표현을 많이 쓰다 보니까 이게 오해를 좀 낳습니다. 어떤 식으로 이해하는 경우가 많냐면, 다음처럼 어떤 점에서 더 높은(값) 쪽으로 가장 가파른 방향의 접선 벡터 아닌가? 하고 느껴지는 경우가 많습니다.

하지만 땡입니다. 이렇게 이해하면서부터 모든 오해가 시작되기 때문에 그레디언트를 수월하게 이해하기가 어렵습니다. 어떤 3차원 도형(2 변수)에서 특정 점에서의 Gradient는 접선처럼 되는 것이 아니라, 가장 가파르게 변하는 방향의 벡터를 x, y 평면에 Projection하는 것 입니다. 그러니까 x,y 평면바닥에 딱 붙어 있고, 위쪽으로의 f(x, y) 방향벡터성분이 없습니다.

요컨대, 요걸 순서대로 들여다보자면,
① x, y 두 개의 2 변수 함수입니다.
② f(x, y)가 특정 값을 갖는 점을 Level Curve라고 합니다. 등고선이라고도 하죠.
③ 그 Level Curve위에 어떤 점에서의 그레디언트는 말이죠, 더 높은 쪽을 가리키는 가파른 접선 벡터를 찾아서
④ xy평면으로 Projection 한 벡터입니다.
그러니까, ②번 등고선을 기준으로 잘라놓고, 하늘에서 보면 이런 식입니다.

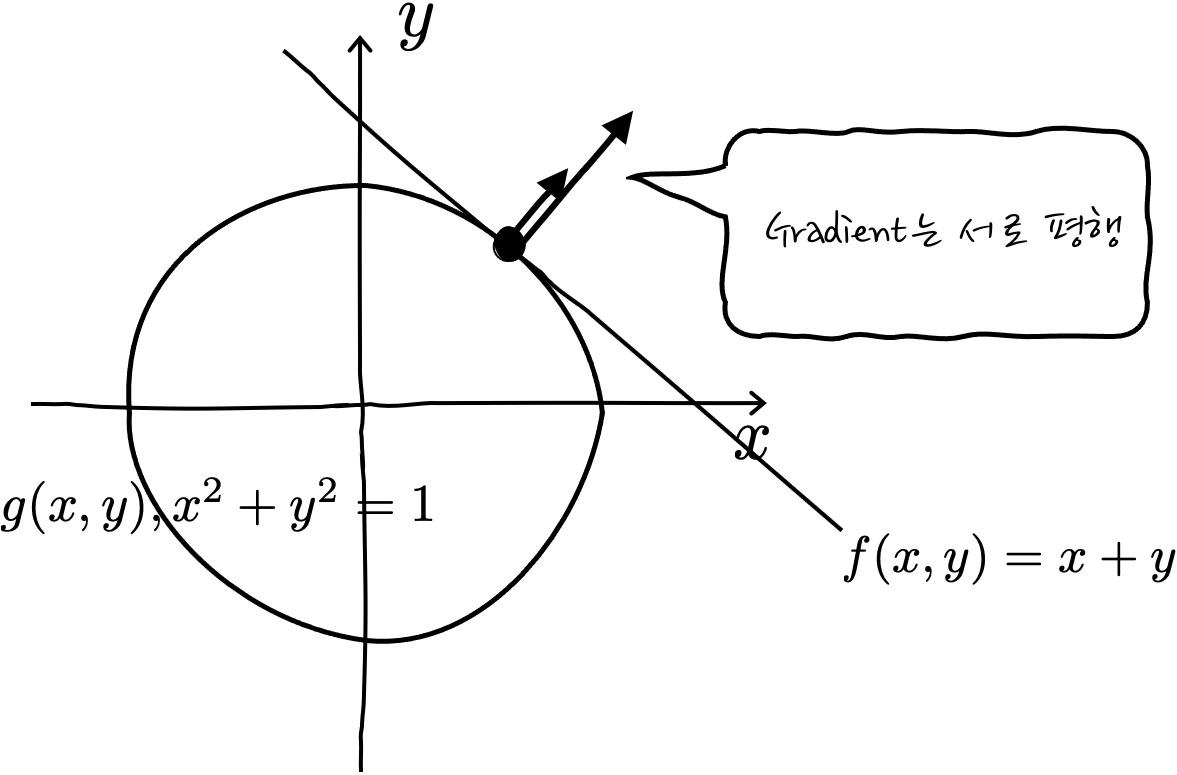
그렇군요. 그러면 예를 이용해서, 몇 가지 연습을 해 봅시다. $x^2 + y^2 = 1$ 의 Gradient는 어떻게 생겼을까요?
원의 방정식을 그려놓고 보았을 때 Gradient는 원의 바깥쪽을 가리키게 됩니다. 엥 왜죠?

이상하게만 느껴질 수 있는 건데, 왜 Gradient가 바깥쪽을 가리키는지 감이 오나요? 이게 Gradient가 x, y 평면으로 Projection 해서 보면 아주 쉽게 이해가 되는데요, $f(x,y) = x^2 + y^2$ 를 그려보면 항아리 모양으로 인데요, 항아리는 반지름이 커질수록 f(x, y)가 더 큰 값이 됩니다.
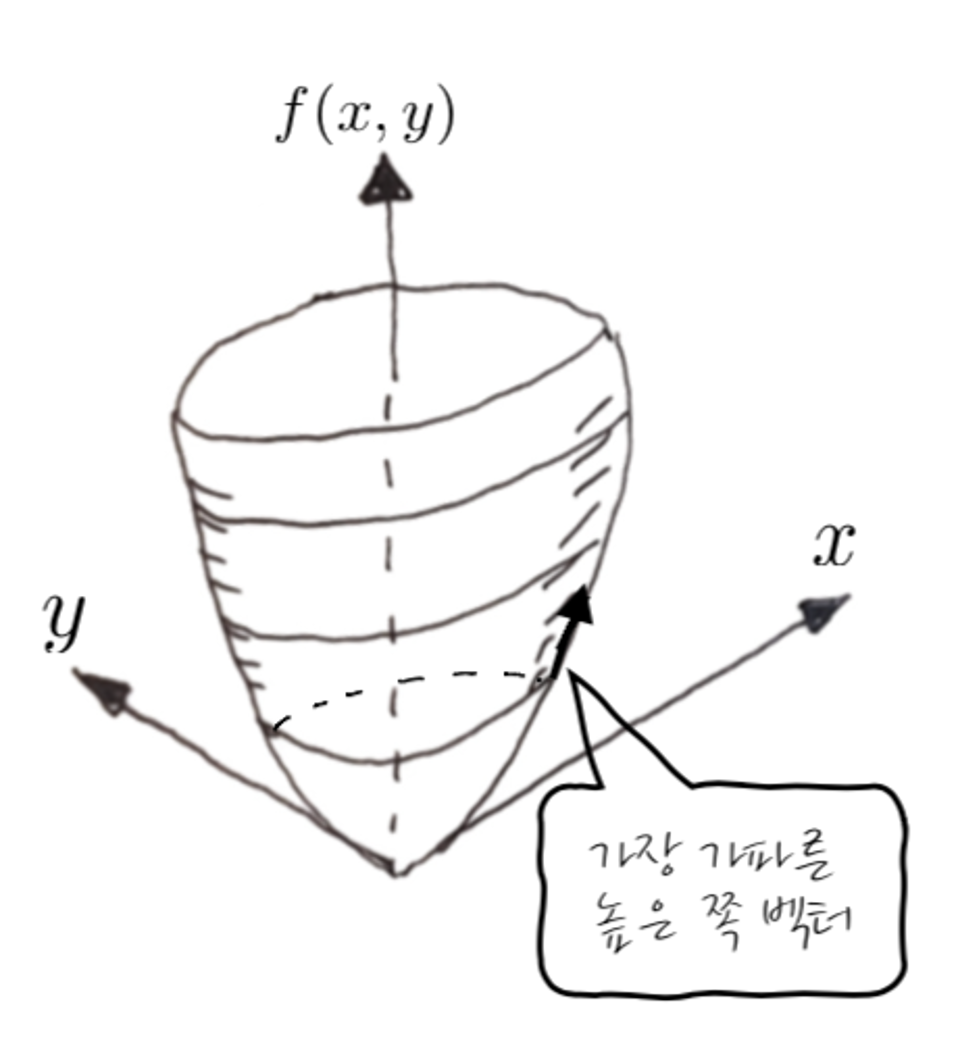
그러니까, 높이 C에서 등고선을 뙇 잘라서 xy평면을 향해 하늘에서 보면, 어느 점에서건 원의 바깥쪽을 가리켜야만 항아리 f(x, y)에 대해서 증가하는 방향이 됩니다. 호옿 그렇군요! 알겠죠? 아항!
실제로 계산해 봐도 $\nabla f(x,y) = <2x, 2y>$ 잖아요? 이 벡터들을 그려보면 xy평면에서 원의 바깥쪽을 가리킵니다.
그러면, 직선에 대해서도 한번 볼까요? 예를 들어서 $f(x,y) = x + y$에 대해서 한번 생각해 보자면 - 등고선이 f(x, y)=0인 경우를 보면

이런 식으로 생겼습니다. 왜 이런 식으로 Gradient가 생겼는지 상상이 되나요? 후훟. 사실상 이 직선도 f(x, y)=0에서의 등고선, 즉 y=-x+C에서 C가 0일 때의 등고선일 뿐, f(x, y) 측면에서 보면 약간 기울어진 평면이 되겠습니다.
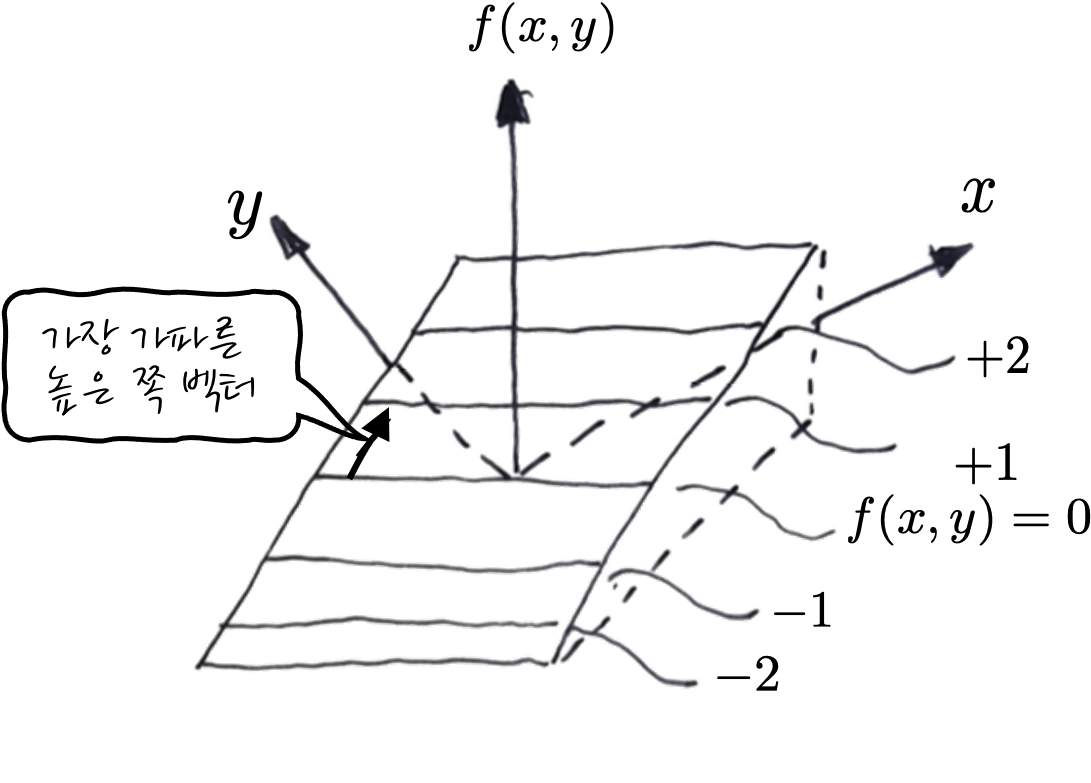
잘 보면 지면 뒤쪽으로 오르막 평면인 셈입니다. 그러니까, f(x, y)가 커지는 오르막 방향으로 Gradient가 생기는 것이 맞는 이야기 겠죠! Gradient를 계산해 보면 $\nabla f(x,y) = <1,1>$ 이잖아요? 아핳. 이제 Gradient 정도는 이해가 잘 되지 않았나 싶습니다. 다음은 긴 이야기니까, 이 정도에서 잠시 화장실에 다녀오셔도 좋습니다.
STEP 2! Gradient가 뭔지는 알았고, 이제 원래의 취지를 달성하기 위해서 두 함수의 공통접선을 구하면 되겠는데 말이죠, 이때, 어떤 함수의 특정한 점에서 접선벡터와 Gradient는 수직Perpendicular합니다. 이 점이 매우 중요한데, 이 성질 덕분에 공통접선벡터를 직접 구하지 않아도 공통 Gradient를 구하면 자연쓰럽게~ 접선과 접점을 구할 수 있게 됩니다. 아니, 근데 왜 공통접선벡터를 안 구하고, Gradient를 고려하는가 하면 공통접선벡터를 구하는 것보다 특정한 점에서 Gradient를 구하는 것이 훨~씬 쉽기 때문입니다. 접선은 dx, dy, dz 모두 전미분을 해야 하지만, Gradient는 ∂x, ∂y, ∂z의 편미분만 하면 되거든요.
자, 그러면 접선벡터와 Gradient가 도대체 왜 수직 하는가가 궁금하게 되는 것이 당연할 텐데요, 어떤 등고선을 고정하기 위해 딱 어떤 Constant로 Fix, 즉 f(x, y, z) = C라고 했을 때, 다변수 함수의 연쇄법칙을 슬쩍 살펴보면, f의 변화율은 각각의 편미분을 이용해서 계산할 수 있습니다. 다변수 함수의 연쇄법칙은 말이죠,
$df(x,y,z) = \cfrac{\partial f(x,y,z)}{\partial x}dx + \cfrac{\partial f(x,y,z)}{\partial y}dy + \cfrac{\partial f(x,y,z)}{\partial z}dz $ 이잖아요? 이게 다변수 함수의 연쇄법칙인데요, f(x,y,z) = C로부터 시작하면 df(x,y,z) = 0 이 됩니다. 결국,
$df(x,y,z) = \cfrac{\partial f(x,y,z)}{\partial x}dx + \cfrac{\partial f(x,y,z)}{\partial y}dy + \cfrac{\partial f(x,y,z)}{\partial z}dz = 0$ 가 되고요, 이걸 벡터의 dot product 형태로 쓰게 되면
$\left(\cfrac{\partial f(x,y,z)}{\partial x}, \cfrac{\partial f(x,y,z)}{\partial y}, \cfrac{\partial f(x,y,z) }{\partial z}\right)
\cdot (dx, dy, dz) = 0$ 로 쓸 수 있겠죠.
즉, $\nabla f(x,y,z)\cdot (dx, dy, dz) = 0$로 표현할 수 있습니다. 이렇다는 이야기는 Gradient와 접선벡터(전미분)가 서로 직교한다는 뜻입니다. 오, 그렇군요.
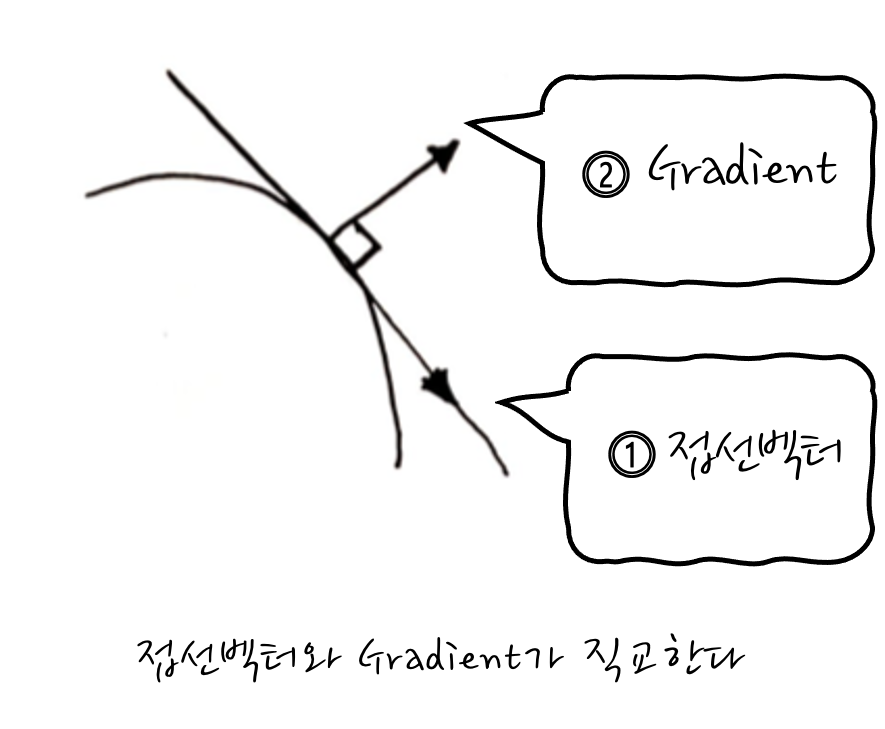
자, 이제 다 왔습니다. 어떤 두 개 함수가 만난다는 것은 접선을 공통으로 공유하기 때문에, Gradient도 공유합니다. 공통 Gradient는 크기가 다를 뿐 같은 벡터라는 이야깁죠. 즉 두 개의 Gradient는 평행합니다. 자, 이제 공통접선을 구하느라고 고생하지 말고 서로 평행인 Gradient를 최대한 이용해 보자고요.
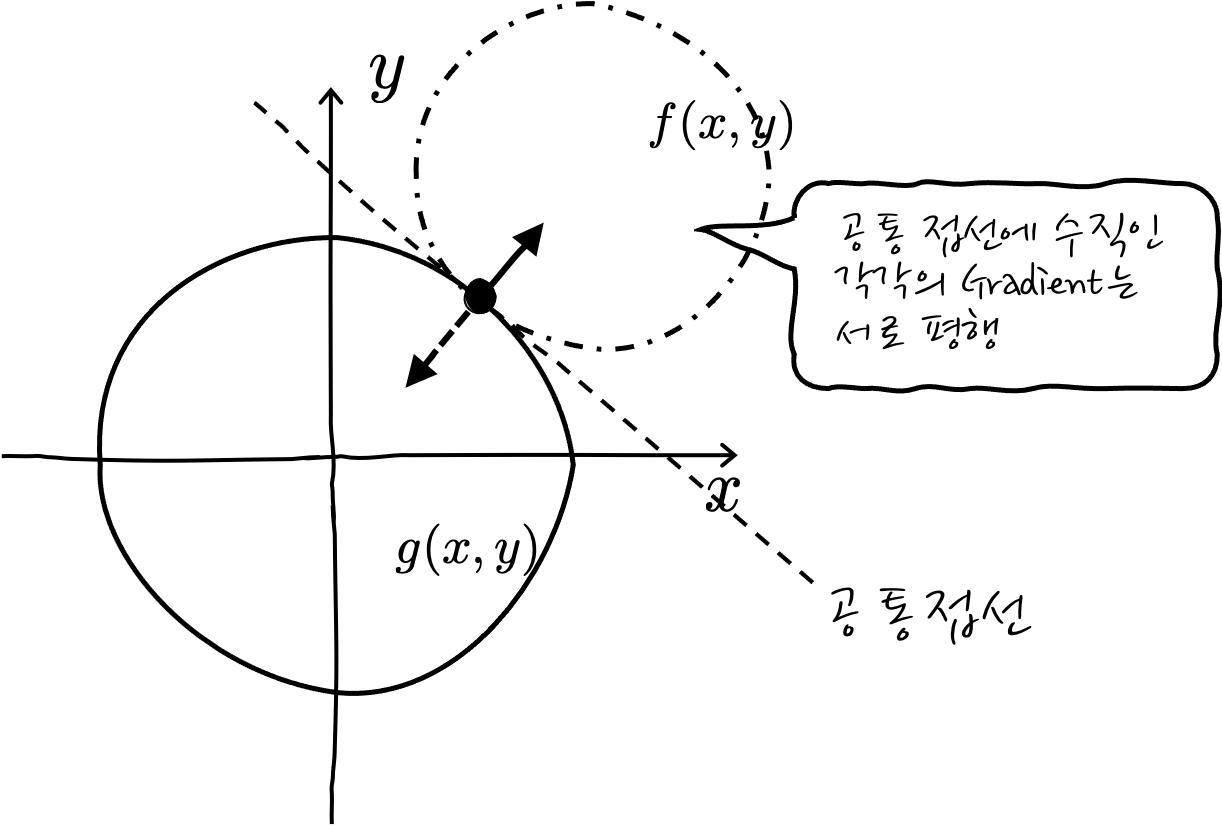
f(x)와 g(x) 두 함수가 있을 때, 접점에서의 두 함수의 Gradient가 평행하다고 표현할 수 있는데, "이것이 바로 라그랑주 승수법의 정체입니다" 일반적으로 $\nabla f = \lambda \nabla g$ 라고 표현합니다. 여기에서 λ가 라그랑주 승수입니다.
자, 그럼 이런 걸 어디에 써먹느냐 하면, 서론이 너무 길어서 잊어버렸을지도 모르겠지만, 최대, 최소값을 구하는 이야기를 하던 중이었잖아요? 어떤 제약사항이 있을 때, 주어진 함수의 최대, 최소값을 구할 때 써먹습니다. 후후.
처음에 들었던 예를 다시 들어서 문제를 하나 풀어보면 어떨까 합니다.
f(x, y) = x+y 일 때, x²+y²=1 조건하에 f(x, y)의 최대 최소값은? 이라는 문제를 풀어보시죠.
참고로, 이럴 때 일반적인 notation으로는 조건, 제약사항등의 함수를 g로 표현을 많이 합니다. 이유는 없고, 그냥 그렇습니다. 췟. 이 문제에서는 원의 방정식이 제약사항 g(x, y)로 표기가 되고요, 이런 문제를 영어로는 "Find Max(min) of f, s.t g"라고 표현하기도 합니다. 여기에서 s.t는 subject to의 약자이고, 어떤 제약에 대하여라고 해석합니다. such that으로 읽기도 하는데, 뭐 어떤 제약에 대하여라는 건 달라지지 않으니까 별 상관없지 않을까 하는 생각입니다.
자, 그러면 g(x, y)를 x,y평면에서 보기 위해서 x² + y² -1 = 0으로 두면 f(x,y)=0인 x,y평면에서 반지름이 1인 원을 볼 수가 있겠고요,
자, 이제 라그랑주 나와라.
$$\nabla f = \lambda \nabla g$$
이 문제에서는 x,y의 2 변수니까,
$$\nabla f(x,y) = \lambda \nabla g(x,y)$$ 로 표현할 수 있겠습니다. 여기에서부터 시작해서 계산해 보면,, <1,1> = λ <2x, 2y>가 되잖아요? 자, 이때 $x = \frac{1}{2 \lambda}, y=\frac{1}{2 \lambda}$ 가 되고요, 그리고 이때의 x, y는 g(x, y)와 f(x, y) 위에 있을 거잖아요?
그러니까, 이걸 대입해서 풀면,
$\cfrac{1}{4 \lambda^2} + \cfrac{1}{4 \lambda^2} = 1$ 이고요, 결국 $\lambda = \pm \sqrt{2}$ 이 되고, 결국 최종 접점은 $x = \frac{1}{2 \lambda}, y=\frac{1}{2 \lambda}$ 에 대입하게 되면, $\left(\cfrac{1}{\sqrt{2}},\cfrac{1}{\sqrt{2}} \right), \left(-\cfrac{1}{\sqrt{2}},-\cfrac{1}{\sqrt{2}} \right)$ 이렇게 구할 수 있습니다. 요 두 점이 두 개의 접점이 됩니다. 그러면 f(x, y)의 최대/최소값을 구해야 하니까, 넣어보면 최대값은 $\sqrt{2}$, 최소값은 $-\sqrt{2}$ 가 됩니다. 오, 아까 본거랑 답이 같군요? 이렇게 풀어보니까, 후후. 쉽죠?라고 생각해 주세요.
STEP 3!
어쨌든 이렇게 풀면 되는데, 이걸 좀 더 있어 보이게 표현하는 방법이 있습니다. 어떤 식이냐면,
라그랑쥬 함수를 $\mathcal{L} = f + \lambda (c-g) $ 이런 식으로 정의하면,
이때, $\nabla \mathcal{L} = 0, \cfrac{\partial \mathcal{L}}{\partial \lambda}=0$ 를 풀면 됩니다. 네?
이게 왜 이러냐면, - ∇f = λ∇g를 다시 한번 자세하게 늘어놓으면 -
$$
\begin{aligned}
& \nabla f = \lambda\nabla g \rightarrow \nabla f - \lambda\nabla g =0 \rightarrow \left.\begin{array}{rl}
\frac{\partial f}{\partial x_1}\left(x_1, \ldots, x_n\right) & -\lambda \frac{\partial g}{\partial x_1}\left(x_1, \ldots, x_n\right) = 0 \\
\frac{\partial f}{\partial x_2}\left(x_1, \ldots, x_n\right) & -\lambda \frac{\partial g}{\partial x_2}\left(x_1, \ldots, x_n\right) =0 \\
\vdots \\
\frac{\partial f}{\partial x_n}\left(x_1, \ldots, x_n\right) & -\lambda \frac{\partial g}{\partial x_n}\left(x_1, \ldots, x_n\right) =0 \\\\
g\left(x_1, \ldots, x_n\right) & =c
\end{array}\right\}\\
\end{aligned}
$$
요런 연립방식을 푸는 것과 같습니다. 이때 $\mathcal{L}\overset{\Delta}{=}f+\lambda (c-g)$로 정의를 하면 마지막 행의 $g\left(x_1, \ldots, x_n\right) =c$를 $\cfrac{\partial \mathcal{L}}{\partial \lambda} = \cfrac{\partial(f+\lambda(c-g))}{\partial \lambda} = c - g = 0$로 표현할 수 있겠습니다. 오. 그러면 이 연립방정식을
$$
\begin{aligned}
\left.\begin{array}{l}
\frac{\partial \mathcal{L}}{\partial x_1}&=\frac{\partial f}{\partial x_1}-\lambda \frac{\partial g}{\partial x_1} &= 0 \\
\vdots \\
\frac{\partial \mathcal{L}}{\partial x_n}&=\frac{\partial f}{\partial x_n}-\lambda \frac{\partial g}{\partial x_n} &= 0 \\\\
\frac{\partial \mathcal{L}}{\partial \lambda}&=\cfrac{\partial (f+\lambda(c-g))}{\partial \lambda} = c-g &= 0
\end{array}\right\} \rightarrow \nabla_{\bar{x}, \lambda} \mathcal{L}_{\bar{x}, \lambda} = 0
\end{aligned}
$$
요런 식으로 λ를 포함해서 Gradient를 한꺼번에 표현할 수 있겠습니다. 결국 간단하게 만들면,
$\nabla \mathcal{L} = 0$와 $\nabla \mathcal{L}_{\lambda} = 0$를 연립하는 것이므로, 라그랑주승수를 Gradient에 포함해서
$\nabla \mathcal{L} = \nabla (f+\lambda(c-g))= \nabla f + \nabla \lambda(c-g)$ 로 한 줄로 이걸 정리할 수 있으니까 이걸 라그랑주 공식처럼 사용하기도 합니다.
풀었던 예시를 다시 한번 이런 식으로 써 보면, f(x, y) = x + y, c-g(x, y) = 1-(x²-y²) 이고,$\nabla \mathcal{L}=\nabla(f+\lambda(c-g))=0$ 이므로
$$
\nabla \mathcal{L}=\nabla(f+\lambda(c-g))=\left[\begin{array}{l}
\frac{\partial}{\partial x}\left( x+y+\lambda\left(1-(x^2+y^2)\right)\right) \\
\frac{\partial}{\partial y}\left( x+y+\lambda\left(1-(x^2+y^2)\right)\right) \\
\frac{\partial}{\partial \lambda}\left( x+y+\lambda\left(1-(x^2+y^2)\right)\right)
\end{array}\right]=\left[\begin{array}{c}
1-2 \lambda x \\
1-2 \lambda y \\
1-x^2-y^2
\end{array}\right]=\left[\begin{array}{l}
0 \\
0 \\
0
\end{array}\right]
$$
을 푸는 것과 같습니다. 결국 이렇게 하면 접선을 구하기 위해서 어려운 길을 가지 않더라도 Gradient를 이용해서 쉽게 접점을 구할 수가 있고, 그러니까 최대, 최소값을 구할 수도 있겠습니다. 아항. 이제는 이해했다는 표정만 지으면 모든 것이 다시 평화로워질 것입니다.

마지막으로 3 변수일 때를 보면, 이제는 f(x, y, z)가 되고요, 3 변수가 되다 보니 등고선이 3차원으로 나타나게 됩니다.
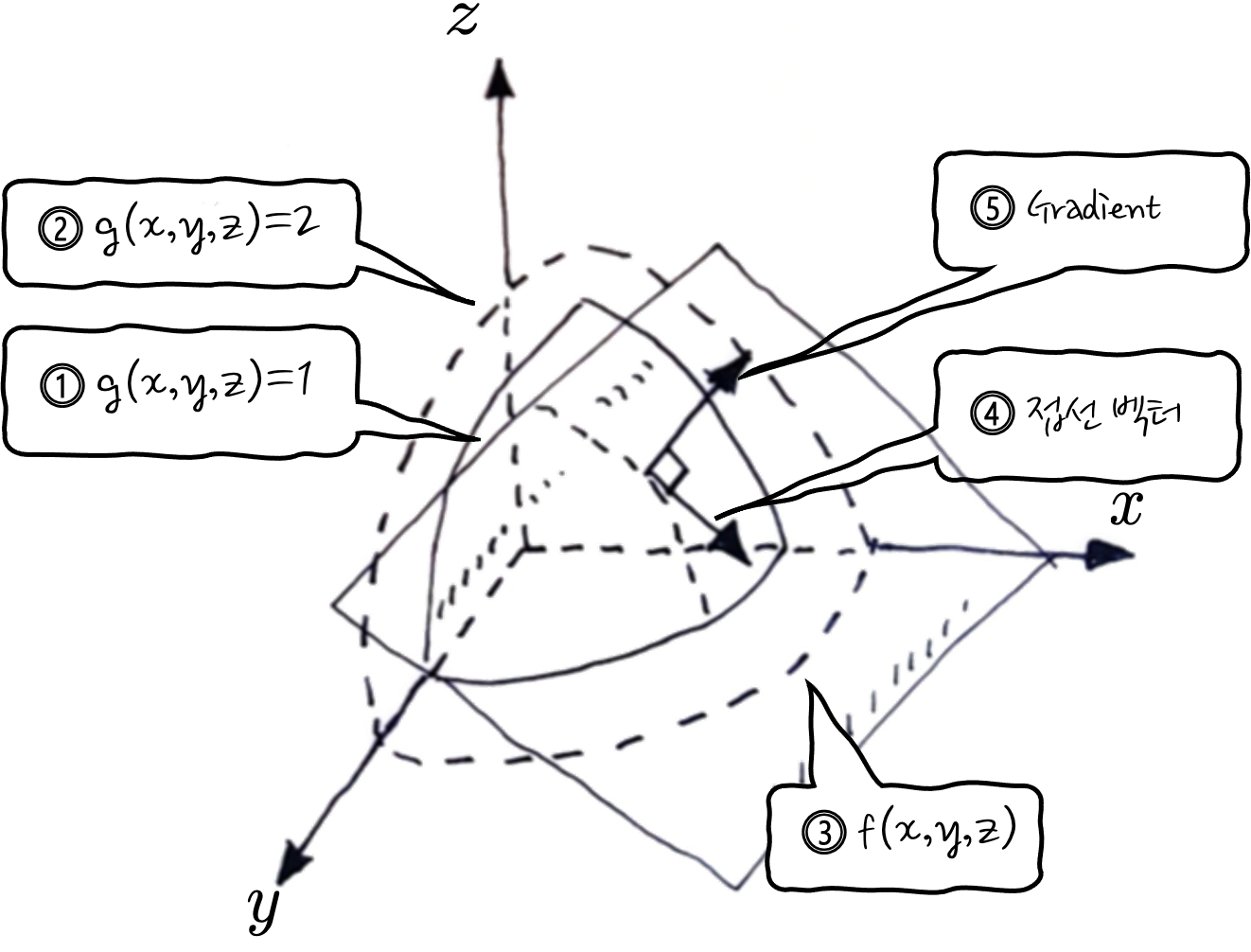
①과 ②는 g에 대한 3차원의 등고선입니다. 참고로 ②의 g가 더 큰 값의 등고선입니다.
③ 최대 최소값을 구할 f입니다.
④ 기울기를 나타내는 접선벡터입니다.
⑤ 접선벡터에 수직하고 중심에서 바깥쪽을 향하는 것이 g의 Gradient 벡터입니다. 왜 바깥쪽이냐 하면 g=1에서 g=2의 등고선 방향을 가리킬 테니까요. 이때 f의 Gradient는 ∇g//∇f 이겠죠. 머
3 변수에서는 우리가 처음에 상상했던 느낌이 좀 살아나는데, 등고선이 3차원(x, y, z)이다 보니까 등고선과 등고선 사이에 가파른 정도에 Gradient가 3차원으로 그려집니다. 이때 f(x, y, z)와의 공통 Gradient를 이용하면 접선을 찾을 수 있습니다. (사실은 접선이라기보다는 접평면이라고 봐야 하겠군요)
이제서야 아아 라그랑주 승수법이라는 게 이런 거구나 하는 실감이 듭니다.

그런데 제약사항이 여러 가지인 경우도 있을 수 있잖아요? 그럴 땐 말이죠, n개의 제약사항이 있다면,
$\mathcal{L}(x, \lambda) = f(x) + (\lambda_1 (c_1-g_1 (x)) + \lambda_2 (c_2-g_2 (x)) +\cdots+\lambda_n (c_n-g_n (x))$
이런 식으로 라그랑주 방정식을 만들어 놓고 Gradient 해서 문제를 풀면 됩니다.

여기에서는 라그랑주 승수법에 대하여 원리를 설명하느라 라그랑주 승수법이 먹히는 조건이 있는데, 그것은 특별하게 이야기하지 않았습니다.
 친절한 데이터 사이언스 강좌 글 전체 목차 (정주행 링크) -
친절한 데이터 사이언스 강좌 글 전체 목차 (정주행 링크) - 

댓글