관측한 데이터만으로 (비모수적으로) 확률분포 추정해서 만드는 방법

내가 관측한 데이터의 분포로부터 확률 분포를 만들어 보고 싶은데, 어떠한 사전 정보나 지식 없이 측정으로만 맨바닥부터 만들려면 어떻게 해야 하는지에 대한 궁금증이 있을 텐데, 조금 이상하지만 그런 방법이 있습니다. 그것을 얘기하다 보면, "음 그렇군" 정도로 넘어갈 수 있을 테니, 조금은 안심입니다. 이런 추정방법을 비모수적 밀도 추정 방법 - Non Parametic Density Estimation이라고 합니다. 

확률분포를 Estimation하는 방법에는 Histogram을 이용해서 추정하는 방법이 가장 간단한데, 이때 Histogram은 bin size 때문에 그 정밀도가 많이 떨어집니다. 많이 봤겠지만요, 막 계단이 생겨 보이거든요. 그리하여 Kernel Density Estimation(KDE)이라는 방법으로 확률분포를 재구성하는 방법을 쓰는데, Kernel Function이라는 것을 이용해서 분포를 Estimation 합니다. Kernel이라는 용어는 발음이 참 근사하다고 생각합니다. 한국어로 번역하면 보통 핵이라고 번역을 하는데 핵 맵다 핵 멋있다 할 때의 매우 강함의 정도를 나타내는 핵이 아니라 원자핵이라던가 세포핵 등의 어떤 것의 중심이라는 뜻 입니다만, 실제 의미는 핵심 함수, 기본 함수, 기저 함수의 뜻에 가깝습니다. 가장 마음에 드는 것은 기저 함수라는 단어인데, 왜냐하면 이 함수를 basis(단위)로해서 합을 표현해서 전체를 표현하고, 또 이 basis(단위)로 분해할 수 있다라는 그런 컨셉이기 때문입니다. 혹시 도움이 될지 모르겠지만, Convolution이라든가, Fourier Transform, Laplace Transform등에서 basis로 사용되는 지수함수를 Kernel이라고 생각하면 조금 이해가 더 잘 될 것 같긴 합니다만  

일단, KDE에서 Kernel function이라는 것은 원점을 중심으로 대칭이고, 면적이 1인 Non-negative 함수로 정의되고요, Gaussian, Uniform 함수 등이 대표적인 커널 함수들입니다. 일단 면적이 1이라는 것은 곱해서 적분을 한다면 특정한 구간만 남기고 나머지 구간을 남기지 않는다는 의미이기도 합니다. 마치 filter같은 의미인데, - 그러고 보니, kernel자체는 filter의 의미도 갖는군요. Convolution에서 filter의 의미를 갖습니다 - 여튼 이 의미는 나중에 더 살펴보기로 하시죠.

참고로  Kernel Function에는 요런 것들이 있습니다. 

딱 봐도 Uniform Kernel 일 때가 가장 간단하니, 이것을 이용해서 KDE를 이해해 봅시다. 

4, 5, 5, 6, 12, 13, 13, 13, 14, 14, 15, 16, 17
Observation이 있다고 하면, bin size를 1로 놓았을 때,

데이터는 이런 식 이겠군요. 히스토그램은 전체 느낌을 알 수는 있지만 여전히 딱딱하군요.

그러면 w=4라고 했을 떄, (w는 Kernel 함수의 Width, Window size라고도 합니다), Window를 1씩 Sliding 하면서 개수를 세어보면 어떨까요.

이런 식인데, 이걸 그려보면 이렇습니다. 

왠지 조금은 더 부드러워졌다고나 할까요.

이 아이디어를 차용해서, 다음과 같이 산수적인 접근을 좀 해보겠습니다. 일단 우리가 w를 계속 Sliding 하는 것을 이걸 수식으로 잘 나타내면 다음과 같은데요, 일단, Uniform Distribution은 $f(x) = \cfrac{1}{b-a}$ 인데요, 높이가 $\cfrac{1}{b-a}$ 이고, 아래 변이 b-a 이면 됩니다. b-a = w, 높이를 1/w로 바꿔서 생각해 봅시다. 

그러면 이걸 방금 우리가 했던 방식대로 Window를 구성할 수 있는데, $-\cfrac{w}{2} \sim \cfrac{w}{2}$ 사이에서는 값이 있고, 아닌 경우 값이 0인 경우인데, 모든 x에 대해서 이걸 고려하자면, $x-\cfrac{w}{2} \sim x+\cfrac{w}{2}$ 에서만 높이 1/w의 값을 갖고, 나머지는 0이 되는 형태로 만들면 Uniform이 됩니다. Kernel 함수를 수학적으로 다시 표현해서 접근한다면,

$K(x)=\left\{\begin{array}{ll}\cfrac{1}{w} : & \left|x-x_{i}\right|<\cfrac{1}{2}w \quad i=1, \ldots, n \\ 0 : & \text { otherwise }\end{array}\right. = \left\{\begin{array}{ll}\cfrac{1}{w}: & \cfrac{\left|x-x_{i}\right|}{w}<\cfrac{1}{2} \quad i=1, \ldots, n \\ 0 : & \text { otherwise }\end{array}\right.$

오, 그럴듯하네요. 자, 직접 계산해 보면 뭔가 나올 테니 한번 보시죠. 아까는 w=5의 경우에 따져봤는데, 이번에는 w=4인 경우로 계산해 보시죠. x=3에서 w=4인 경우에 계산의 편의상 $\cfrac{1}{w}$를 빼고 Sliding을 따져보면,
(데이터는 4, 5, 5, 6, 12, 13, 13, 13, 14, 14, 15, 16, 17 이었었었습니다)

$K\left(\cfrac{|3-4 \mid}{4}\right)+K\left(\cfrac{|3-5|}{4}\right)+K\left(\cfrac{|3-5|}{4}\right)+\ldots+K\left(\cfrac{\mid 3-17|}{4}\right) \\= K(1/4) + K(2/4) + K(2/4) + \cdots + K(14/4)$
$ = 1 + 0 + 0 + \cdots + 0 = 1$   
$\because \cfrac{|x-x_i|}{w} < \cfrac{1}{2} $이외에는 모두 0이니까요.
요렇게 Kernel 함수를 구성하면 되겠습니다. 오호, 이렇게 하면, 3의 주변에는 1개 정도의 데이터가 관찰되었겠군요.라고 읽어주시고요. 그 정도의 밀도라고나 할까요.라고 이해해 주시면 좋겠습니다. 

이해를 돕기 위해서 x=4에서도 한번 볼까요? (w는 4로 같아야겠지요)

$K\left(\cfrac{|4-4 \mid}{4}\right)+K\left(\cfrac{|4-5|}{4}\right)+K\left(\cfrac{|4-5|}{4}\right)+K\left(\cfrac{|4-6|}{4}\right)+\ldots+K\left(\cfrac{\mid 4-17|}{4}\right) \\= K(0) + K(1/4) + K(1/4) + K(1/2) + \cdots + K(13/4)$
$ = 1 + 1 + 1 + 0 \cdots + 0 = 3$   

4 주번에는 3개 정도 데이터가 있군요.


자, 그럼 모든 관측 데이터 $x_i$에 대해서 합을 구하니까 1개의 x에 대해서, 

$\sum\limits_{i=1}^{n}\cfrac{1}{w} K\left(\cfrac{\left|x-x_{i}\right|}{w}\right)$ 로 나타낼 수 있겠습니다.  

그리고, 모든 $x_i$에 대해서 합을 구했으니까, n으로 나눠서 크기를 평균을 내서 보자구요. 

$\sum\limits_{i=1}^{n} \cfrac{1}{wn}K\left(\cfrac{\left|x-x_{i}\right|}{w}\right)$ 

여기에 이어 모든 x에 대해서 합을 구하려면 

$\sum\limits_{x}^{all \, x} \sum\limits_{i=1}^{n} \cfrac{1}{wn}K\left(\cfrac{\left|x-x_{i}\right|}{w}\right)$

요렇게 표현할 수 있겠습니다. 호, 그렇군요. 
이걸 그래프로 보면, 아까랑 그린 비슷한 형태가 나옵니다. 

 

이게 Uniform을 Kernel로 한 Kernel Density Estimation KDE입니다. 별거 아니죠.

자, 그러면 Kernel을 이번에는 Uniform대신에 Gaussian으로 하게 되면 어떻게 될까요?

각 Gaussian의 Sliding 값들의 합이 되겠군요. Uniform과 같은 원리인데 더 부드러운 곡선 형태의 Estimation이 되겠습니다. 

$K(u) = \cfrac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}u^2}$ 를 Kernel function으로 쓰게 되면, $\cfrac{1}{nw}\sum\limits_{i=1}^{n}\cfrac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}(\frac{x-x_i}{w})^2}$가 됩니다. 지수 함수의 지수 안에 들어갈 절댓값은 제곱했으니까 없어지고요.

결국 결과는 이런 식이 되는데, 꽤나 부드러운 Density Function이 되겠습니다. 부드러운 Density를 보여줄 순 있습니다. 사실 그다지 쓸모 있는지는 저는 잘 모르겠습니다만. 데이터만 가지고 분포를 Estimation 했다는 뭐 그런 의미를 갖겠습니다. 

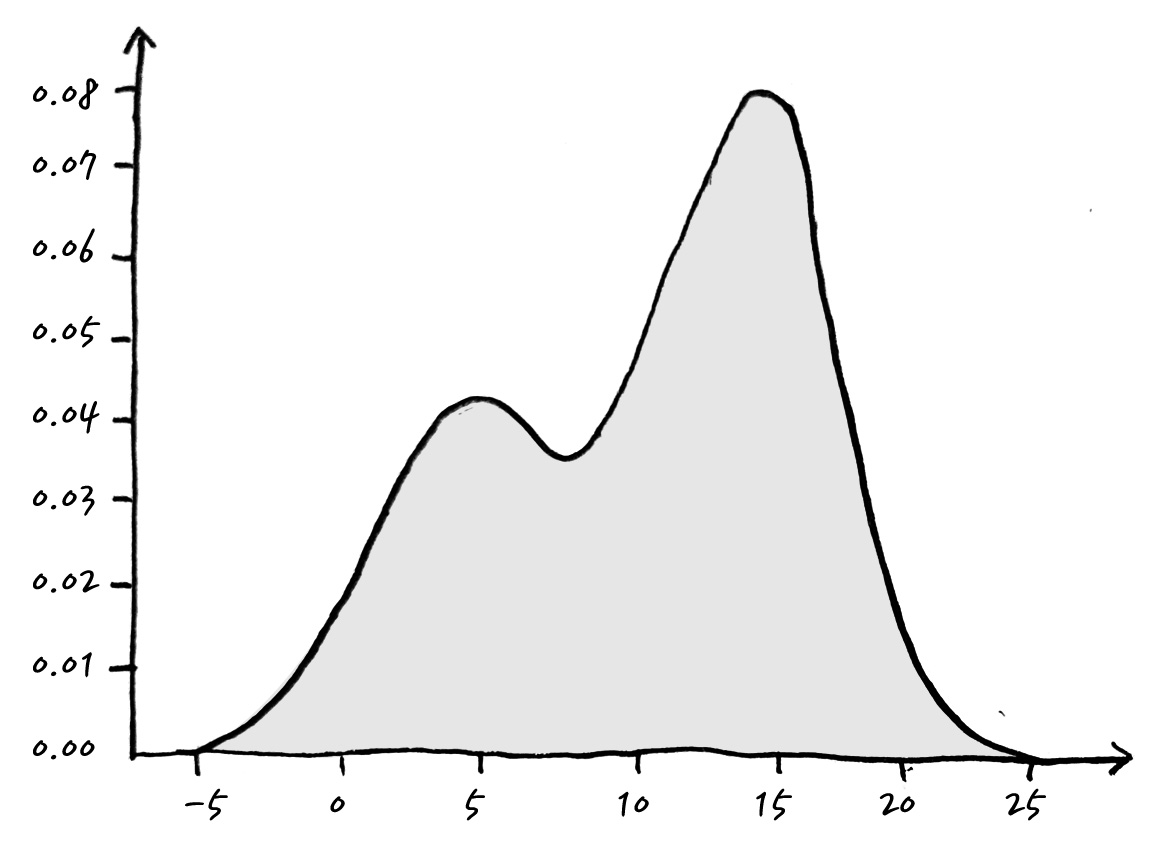
짠! 꽤나 그럴듯한 pdf가 만들어졌군요! 이렇게 함으로써, Observation으로 부터 대충 이렇게 생겼을 것이다 하는 pdf를 비모수적 방법으로 만들어 낼 수 있습니다. 


확률분포를 추정하기 위해 얼마나 많은 고급 테크닉들이 - 통계 공부를 꽤 한 후에 알게 되는 - 사용되는지 이것만 봐도 알 수 있으리라 생각합니다. 하지만, 너무 걱정하지 않아도 됩니다. 이제부터 알면 되니까요. 그런 걱정은 집어치워도 되지 않을까 합니다. 

Gaussian Kernel을 이용할 때, 적당한 Window Size로 잘 정해야  Estimation 할 수 있을 것 같은데,  $w = \left( \cfrac{4\sigma^5}{3n}  \right)^{\frac{1}{5}} ≒ 1.06\sigma n ^ {-\frac{1}{5}} $ 이렇게 계산하면 된다고 하는데, 어떻게 이런 연구결과가 나왔는지는 참으로 알 수 없습니다만, 그런대로 꽤 쓸모 있는 정보인 것 같습니다.