정보이론의 정보를 일반적으로 설명할 때에는 다음과 같은 설명이 주를 이룹니다. 정보는 놀람의 정도 그러니까, 놀라운 일일수록 큰 정보랍디다. 아니, 나는 아무리 큰 정보라도 별로 안 놀라는데...? 싶습니다. 심장이 쫄깃 거릴 정도면 아주 큰 정보인가 싶은데, 어쨌든 놀랄수록 큰 정보라는 말이 무슨 말이냐 하면 예측 못할수록 놀랍고, 큰 정보라는 의미랍니다. 그렇다면 이 예측이 어렵다는 것은 어떻게 측정할 수 있을까 하면, 발생할 확률로 측정이 가능하답디다. 발생할 확률이 작을수록 놀랍고 정보가 크다라는 말과 같다고 합디다. 음. 괜찮은 설명이긴 한데.. 아! 그렇구나 하는 느낌이 없습니다. 만.
왜 이게 잘 모르겠냐면, 일반적인 한국인에게 어떤 사건이 정보량이 크다는 말은 이 정보가 유용하다는 말이라고 생각하니까요. 즉, 정보량이 많다고 함은 유용함이 가득하네? 라는 의미로 통하게 되니까 정말 헷갈릴 수밖에 없다고요. 결국에는 그런 식으로 표현할 수도 있겠구나 싶기도 한데, 어쨌든 처음 이걸 맞닥트렸을 때에는 좀 어렵게 느껴집니다.
자! 그럼, 정보는 말이죠~ 이런 겁니다.
나올 수 있는 모든 사건의 조합중 어떤 사건이 벌어졌는지 맞추기 위한 질문을 하고 난 후, 답변으로 받는 것이 정보입니다. 즉, 질문을 하고 얻는 답변이 정보입니다. 맞죠? 정보. 이때의 정보는 예/아니오 로만 구성됩니다.

어떤 것을 맞추기 위해 질문을 많이 해서 답변(정보)을 많이 얻어야 하면 큰 정보, 질문을 적게 하고 답변(정보)을 적게 얻어도 되면 적은 정보입니다. 같은 맥락으로 이걸 양으로 따진다면, 질문을 많이 해야 해서 얻어야 하는 답변(정보) 개수가 많아야 하면 정보량이 많다. 질문을 적게 해도 돼서 얻어야 하는 답변(정보)의 개수가 적어도 되면 정보량이 작다고 말할 수 있겠습니다.
결국 정보는 얻어내는 답변이고, 정보량은 답변수입니다. 이렇게 생각하면 일적으로 생각하는 정보와 느낌이 비슷하게 됩니다.
지금 방금 말한 그대로 정보에 대해서 정보량을 측정하게 되는데, 예/아니오로 답해야만 하는 질문을 해서 몇번 만에 어떤 사건이 벌어졌는지 알아낼 수 있겠는가? - 다른 말로는 불확실성을 모두 해소할 수 있는가? - 에 대한 것인데, 불확실성을 해소한다는 의미를 되짚어 보면, "예"라는 정보는 정보를 얻은 사람에게 어떤 불확실성을 제거해 줍니다. 가능한 두 선택지 가운데 어느 하나가 답이라는 것을 알게 되기 때문입니다. 물론, "아니오"라는 답도 불확실성을 제거해 주는데 답이 질문에 대한 반대편이 답이라는 것을 알 수 있기 때문입니다. 캬.
자, 이렇게 질문을 해서 정보를 얻은 횟수를 몇 번? = 몇 bit라는 식으로 bit 단위로 정보량을 측정합니다. 정보량은 이 질문과 답변을 통해서 어떤 일이 벌어졌는지 알아 낼 수 있는 최소의 답변(정보)의 수라고 할 수 있겠습니다.
여기에서 한가지 짚고 넘어가야 하는 점은
질문의 횟수 = 답변(정보)의 횟수라는 점인데, 뭐 당연한 이야기겠죠. 여러 다른 설명등에서는 질문수를 기준으로 따지는 경우가 많습니다만.
정보량을 어떤 식으로 측정하는지 예를 보면 쉬운데, 특별히 더 얻기 어려운 정보가 없는 경우를 먼저 한번 보시죠. 한마디로 모든 사건이 Uniform 한 확률을 가질 때의 경우입니다. 주사위가 최적의 케이스겠군요.
주사위를 던지는데, 주사위 눈이 4이었다는 것을 알아내 보시죠. 어떻게 하면 좋을까요? 사실 예/아니오로만 답할 수 있기 때문에 반씩 쪼개기 전략이 가장 유효합니다. 자, 가봅시다.
질문1) 3보다 크거나 같나요? 예
질문2) 5보다 작거나 같나요? 아니오
질문3) 4보다 크거나 같나요? 예
답 : 4
보통 이런 식으로 4가 나왔는지 알아내겠죠? 이게 바로 반씩 쪼개기 전략입니다. 흠. 별거 아니죠? 질문을 3번 하고 정보를 3개 얻어서 답을 맞히는데, 사실 모든 다른 경우의 수 1, 2, 3, 5, 6에 대해서도 3번의 정보를 얻으면 맞출 수 있습니다.
이게 주사위로 하려니까, 경우의 수가 많아져서 4까지 있는 정사면체 주사위로 바꿔서 한번 보시죠.

A, B, C, D 어떤 면이 나왔는지 알아맞추기 위한 정보 획득 전략도 마찬가지로 반씩 쪼개기로 접근하면 됩니다.

자, 이게 반씩 쪼개서 보니까 2개 질문이면 모든 정보를 획득할 수 있겠군요? 이것의 의미는 2개의 경우(예/아니요)를 갖는 정보를 2번 질문해서 정보를 얻으면 모든 사건을 맞출 수 있다는 의미입니다. 다른 말로는 2번 만에 불확실성을 모두 제거한다는 의미인데, 말은 어렵지만 그림으로 보면 불확실성을 제거한다는 의미를 쉽게 이해할 수 있습니다.

자, 어쨌든 이걸 있어보이게 표현해 보도록 하시죠.

모든 경우가 같은 확률을 가진다면 계속 반쪽으로 쪼개는 전략을 이런 식으로 표현할 수 있겠습니다.
그러면 이것은 2가지 중 하나를 선택하는 경우는 1번 질문하면 2가지로 경우가 나뉘고, 2번 질문하면 4가지로 경우가 나뉘니까, 질문이 추가될 때마다 전체 경우의 수는 2배가 됩니다. 이렇게 따지면 좀 불편하니까 log를 이용해서 표현해 보면,

이런 식으로 표현될 수 있겠습니다. 그러면, 질문수(=답변수)는 정보량이라고 했으니까

이렇게도 표현할 수 있겠습니다.
이걸 확률로 표현할 수가 있겠는데, 그 확률이라는게 모두 같은 확률이기 때문에 1을 전체 경우의 수로 나누면 확률이 됩니다. 즉, 다음과 같은 식으로 접근해 볼 수 있겠습니다.

그러니까, 확률로 확실하게 표현해 주면

이런 식이 되겠군요. 이제부터 정보량을 I로 표기하면!

이런 식으로 있어보이게, 멋들어지게 표현할 수 있겠습니다.
먼저 A, B, C, D 모두 같은 확률일 때는 A, B, C, D모두 0.25 확률이니까 어느 경우라도 $I(x) = -log_2 {\cfrac{1}{4}} = 2$ bit입니다. 질문-답변(정보)가 2회잖아요? 그림의 계산결과와 같군요.
자, 여기에서 우리가 Uniform한 경우라고는 했지만 확률로 정보량을 표시하기 시작했잖아요? 그러면, 사건들이 Uniform 하지 않은 경우에는 어떤 일이 벌어질까요? 여기서부터 매우 중요한 정보획득에 대한 사고방식을 똑같이 적용하는데, 이걸 어떤 식으로 정보를 얻을 수 있는지를 보면 반씩 나눠서 질문하는 전략이 다시 똑같이 적용될 수 있습니다. ★ 이 생각 방식이 매우 중요합니다.
자 이번엔 변형문제로, 좀 특별한 주사위가 있다고 칩시다.

이런 식의 A,B,C,D가 나올 확률이 다른 주사위인데, 이건 어떤 식으로 질문을 해서 정보를 얻으면 좋을까요?
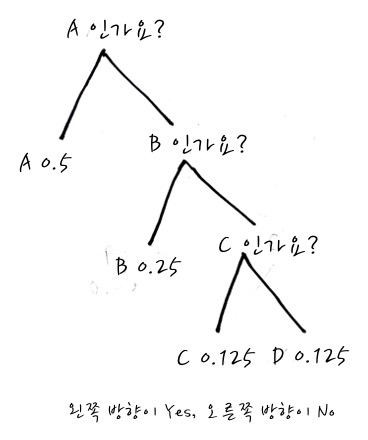
이때에는 굳이 AB인가요로 나누지 않고, A와 BCD로 나누어서 알아보는 전략을 취하는 편이 낫습니다. 불확실성이 제일 많이 제거되는 방향으로 하는 것이죠. 나머지도 B와 CD로 나누면 0.5와 0.5로 나뉘게 되니까 효율적이겠죠.
자, 정보량을 측정하기 위해 질문수를 보면
A : 1 bit
B : 2 bit
C : 3 bit
D : 3 bit 가 되겠지요?
당연한 이야기지만, C와 D가 정보량이 더 크군요? 확률도 작고요. 후후.
요컨대, 사람의 성격에 따라 다르겠지만, 특히 한방을 노리는 사람의 경우, 확률이 더 작은 경우에 더 정보량이 크니까 더 중요하고 그것부터 확인해봐야 하겠다는 느낌도 있을 수 있는데, 실은 더 확률이 크고, 즉, 정보량이 작아 자주 출현하는 것을 찍어서 맞출 가능성이 더 큽니다. 불확실성이 작거든요. 그러니까

정보량이 크면 그 정보는 알아내기에 더 불확실하다는 뜻일 뿐입니다. (더 많은 질문을 해서 답변(정보)을 얻어야 한다는 뜻입니다) 또 다른 말로는 더 많은 정보를 얻어야 한다는 것은 확률이 작다는 말이기도 합니다.
그런데, 이야기가 여기에서 끝나면 정보량이란 그런 거구만. 상식으로 알고 있으면 참말로 좋아요하고 끝나면 좋을 텐데, 세상이 그렇게 녹록하지는 않습니다요. 이렇게 확률이 서로 달라서 정보량이 각기 다를 때 이 전체 경우의 수에 대한 평균 정보량을 구하면 이게 엔트로피 Entropy라는 겁니다. 아~ 평균적으로 이 정도의 질문(답변정보)이 필요하구만 이라고 생각하고, 그 정도의 평균적으로 불확실하구먼 이라고 간주하면 되겠습니다.
엔트로피는 평균이니까 다음과 같이 구할 수 있겠습니다. - 이걸 노리고 바로 전에 평균을 살펴보았는데, 조금 도움이 되길 바라겠습니다. -
$$ H(x) = \sum I(x) P(x) = -\sum \left(log_2{P(x)}\right) P(x) $$
그러니까, 각각의 정보량에 그에 해당하는 확률을 곱하면 이게 엔트로피입니다. 아니, 엔트로피라는 용어가 참으로 멋지긴 한데, 이걸 왜 하나 싶죠. 그냥 하는 건 아닐 테니, 더 자세하게 음미해 볼 필요가 있지 않을까 생각합니다.
엔트로피의 의미는 정보량의 평균이니까 정보량과 마찬가지로 클 수록 전체적으로 봤을 때에 얼마나 불확실성이 크냐, 예측하기 어렵냐, 얼마나 정보가 많이 필요하냐의 의미와 같습니다. 불확실성의 평균의 측정이니까요.
그런데, 더 재미있는 사실은 엔트로피는 최대값이 있다는 것입니다. 이게 평균정보량-엔트로피를 볼 때 자주 보게 되는 그래프인데요, 잘 보면 최대값이 있죠.
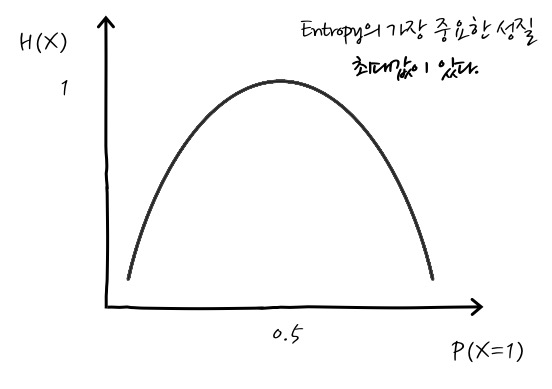
그러면, 언제 최대값을 갖느냐 하면 모든 사건에 대한 확률이 같을 때 엔트로피가 최대가 됩니다. 이것은 라그랑주 승수법 - 휴, 이럴 줄 알고 라그랑주 승수법을 미리 살펴봤으니 얼마나 다행인지 모릅니다. - 으로 최대값을 구할 수가 있습니다. 간단하게 언급하자면, 제약사항은 확률의 합이 1 임을 적용해서 $- \sum \limits_{i} \left(log P(x_i)\right) P(x) + \lambda\left(\sum\limits_{i}P(x_i) -1\right)$ 을 풀면 됩니다. - 결론만 이야기하자면, 모든 확률이 같을 때 최대이고요, 4면체 주사위가 모두 같은 확률일 때를 예로 계산을 해보면
$ 2 \times - log_2 \cfrac{1}{4} + 2 \times - log_2 \cfrac{1}{4} + 2 \times - log_2 \cfrac{1}{4} + 2 \times - log_2 \cfrac{1}{4} = 2$ bit이고요,
4면체 주사위가 예시와 같이 다른 확률일 때에는 이미 계산해 둔 것을 이용해서 계산해 보면,
$ \begin{aligned} & P(A)\times I(A) + P(B) \times I(B) + P(C) \times I(C) + P(D) \times I(D) \\ = & 0.5 \times 1 + 0.25 \times 2 + 0.125 \times 3 + 0.125 \times 3 \\ = & 1.75 \end{aligned} $
즉, 1.75bit 입니다.
그쵸? 서로 다른 확률일 때의 엔트로피가 모두 같은 확률일 때 보다 더 작습니다. 이 이야기는 확률이 서로 다를 때에는 질문을 잘해서 정보를 잘 얻으면 더 쉽게 맞출 수 있다는 의미입니다.
다른 의미로는 엔트로피는 뭔가 "불확실해서 뭔지 모르겠다"는 것이니까, 어느 정도로 모르겠는지 불확실성을 수치로 나타낸 것이라고 생각하면 편리할 수 있겠습니다. 엔트로피가 크면 알아내기 어렵고, 엔트로피가 작으면 알아 좀 수월하다. 뭐 그런 셈입니다.
극단적 예시를 들자면 동전에서 앞면 1만 나오는 있다면 이 경우에는 항상 1이 나오므로 엔트로피가 0입니다. 전혀 불확실하지 않으니까요. 이런 의미로 엔트로피에 대한 설명을 다음과 같은 그림으로 설명하는 경우가 많은데요,
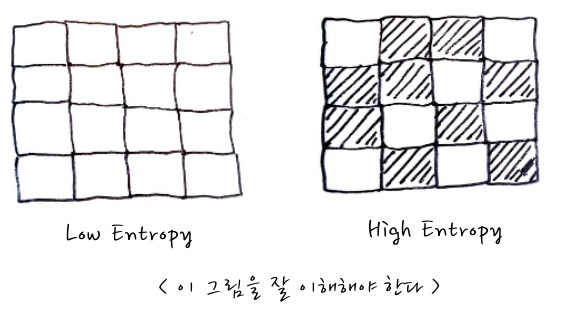
이 그림을 설명할 때, Low Entropy는 불확실성이 적은 경우, 즉, 예측하기 쉬운 경우, High Entropy는 불확실성이 큰 경우, 즉, 예측하기 어려운 경우를 비유하면서 설명하거든요. 음. 그렇군 싶은데, 그림을 정확하게 이해해 보자면, 다음과 같이 이해해야 합니다. 이 Entropy그림은 사건들의 결과를 늘어놓고 보면 결국 이런 식으로 보인다는 뜻입니다.
이 그림은 각 사각형들을 사건의 Slot이라고 생각하고 이 사건이 계속 발생하면 결과적으로 어떤 모양새가 될 것인가로 이해하면 좋겠습니다.
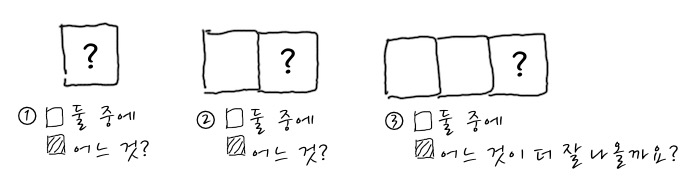
각 사각형에서 첫 번째 칸, 두 번째 칸, 다다다닥 계속적인 사각형이 연속되었을 때, 만일 흰색이 나올 확률이 0.9, 검은색이 나올 확률이 0.1일 때 각 칸에서 무엇이 더 많이 나올까요? 당연히 흰색이 많이 나오겠죠. 이 경우가 Low Entropy입니다. 정보량의 평균, 엔트로피가 더 작다는 의미이고요. 만일 흰색이 나올 확률이 0.5, 검은색이 나올 확률이 0.5라면 High Entropy입니다. 평균정보량이 최대입니다. 뭐가 나올지 모르겠다는 의미입니다. 그런 의미에서라면 이런 식의 사건을 계속적으로 관찰했을 때 다음과 같은 결과가 나온다는 것입니다.
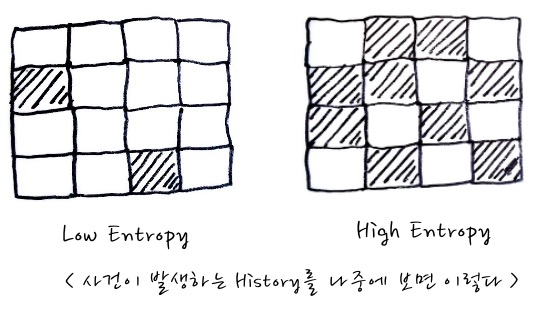
그러니까, 사건 발생을 잘 관찰하면 말이죠, Low Entropy인지 High Entropy인지, 즉 예측하기 쉬운 편인지, 예측하기 어려운편인지를 알 수 있다는 의미입니다. 엔트로피가 클수록 전반적으로 무질서해 보이겠죠.
이런 이야기를 어디에 써먹을꺼냐 하고 물어본다면 "이걸 알게 되어서 행복하다면 지금까지는 OK"입니다.라고 할 수도 있겠고, Entropy 크기에 따라 뭔가를 판단하는 데 사용하기도 하는데, 예를 들면 의사결정나무 모형등에서 Entropy가 크면 불순도가 크다고 판단하기도 합니다. 그건 차차 그런 걸 만나게 되면 다시 이야기하도록 하시죠.

다시 한번 정보를 정리하자면 불확실성이 커서 정보를 많이 얻어야 하는 것은 확률이 작습니다. 이럴 때 그 사건은 정보량이 크다고 표현한다는 점 잊지 않았으면 합니다.

정말 긴 이야기가 되었지만, 다른 어려운 말은 다 잊고, 정보량이 클 수록 불확실하다. 그러므로, 평균정보량 즉, 엔트로피도도 마찬가지다. 고 생각하면 가장 손쉽게 이해할 수 있겠습니다.

지금은 밑이 2인 로그를 다뤘는데 그 이유는 일반적으로 정보를 저장 / 통신하는 전자기기의 데이터는 2진수로 이루어져 있기 때문에 bit로 측정하기 위해서 그렇습니다. 하지만 bit로 측정하지 않고, 어느 정도의 불확실한 양이 많냐를 따질 때에는 굳이 2인 로그를 다루지 않고, 자연로그도 사용합니다.

섀넌님께서 이 정보이론을 구축했는데, 굳이 정보를 예/아니오의 bit로 따진 이유는 메세지를 압축할 때 어떤 식으로 압축을 해야 더 작은 메세지로 압축할 수 있겠는가에서부터 시작했기 때문입니다.

섀넌님께서 최초에 통신에 적용한 정보이론을 정리할 때에는, 주어진 정보를 통신하거나 기록하는데 최소한 몇 비트의 데이터가 있으면 좋을까 하는 문제에 대하여, 필요 없는(여분의) 부분을 제거한 본질적인 정보의 양으로 엔트로피로 정의했습니다. 원래의 정보를 잃지 않게 데이터압축을 하려고 할 때에는, 그 압축의 한계가 엔트로피가 되는 것을 증명했고요. 즉, 아무리 이상적인 데이터 압축을 하더라도 Entropy이하로는 압축할 수없고, Entropy 이하로 압축한 경우에는 원래의 정보를 제대로 복원할 수 없다는 것을 증명했습니다.
 친절한 데이터 사이언스 강좌 글 전체 목차 (정주행 링크) -
친절한 데이터 사이언스 강좌 글 전체 목차 (정주행 링크) - 

댓글