확률분포들의 족보에 관한 관계 보고서

사실 요즘 들어 족보가 무슨 의미가 있는가. 족보라는 단어 조차 들어 본 지 오래되었네요. 보통 족보라는 건 씨족의 혈연관계를 체계적으로 나타내는 것이고, 체계적이다 못해 심지어 이름도 돌림자를 따라서 대충 비슷한 느낌이 드는 것이 보통인데, 확률 분포는 돌림자도 없고, 아무렇게나 이름 지어진 것 같은 들쑥날쑥한 족보라서 머리에 딱 들어오지는 않지만, 그래도 이렇게라도 확률분포들끼리의 관계성을 정리하면 조금 더 확률분포가 친근하게 느껴질 수가 있지 않을까 생각합니다. - 사실 다시 한번 생각해 보면 분포들이 어느 날 갑자기 나타나서 누군가가 정리한 것이 아니라, 오랜 세월에 걸쳐 발견되거나 제안될 때 그때그때 이름을 붙이다 보니, 그렇게 된 것 같다고 생각합니다. 조금은 누군가 정리해 줬으면 더 좋았을 텐데 말이죠 -

확률분포의 족보를 대충 그려보면 다음과 같습니다.

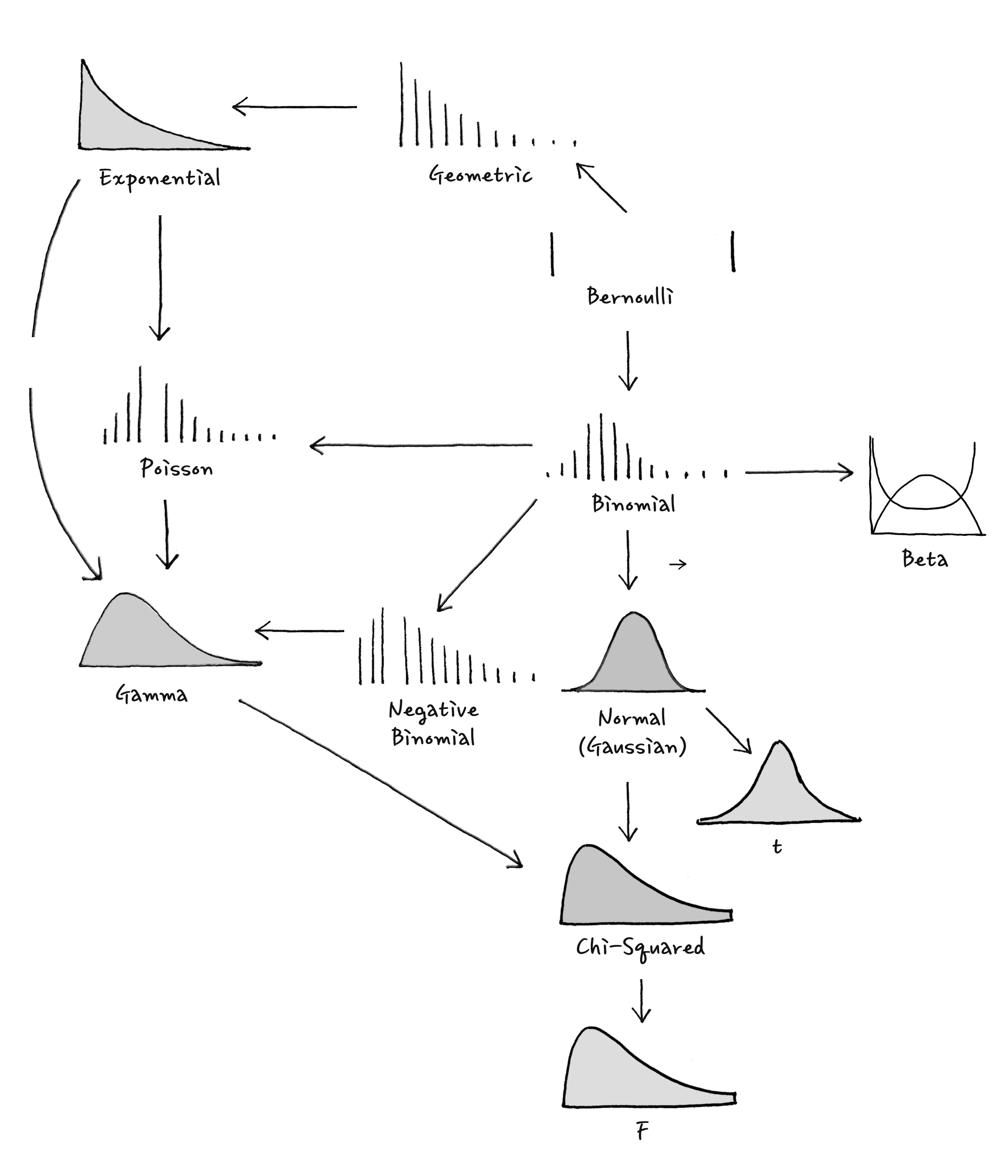
음 그려놓고 보니까, 주요한 분포들이 대단히 많이 있지는 않군요. 그래도 이런 확률분포들이 어떤 관계를 갖는지를 정리하기 위해서 확률분포들을 다시 한번 족보로 정리하면 머릿속이 맑아질 것 같습니다. 관계를 잘 보기 위해서 번호를 붙여보겠습니다.

➊ 이 모든 족보의 시작은 Bernoulli분포로부터 시작됩니다.  Beroulli분포는 성공/실패로만 이루어져 있는 분포입니다.

➋ Binomial이항분포는 n번의 시행 횟수 중에 p의 확률을 가진 사건의 발생수가 확률변수입니다. 이 분포는 성공/실패로만 이루어져 있는 Bernoulli확률변수의 합입니다. 중요한 점은  사건의 발생수가 확률변수입니다.

참고로, Hyper Geometry초기하분포는 p의 확률을 가진 사건의 발생수가 확률변수이며 Binomial과 똑같습니다만, 비복원인 경우입니다. 그러니까, 이미 발생한 것은 다시 발생하지 않는 경우입니다. 예를 들어 주머니에서 공을 꺼내는 경우인데, 공을 꺼낸 후에 공을 다시 넣지 않고, 꺼내는 경우입니다. -초기하분포도 적률생성함수가 초기하함수꼴을 갖고 있는데, 초기하함수의 특수한 꼴이 기하함수이기 때문에 초기하함수라고 (그러니까 슈퍼기하함수?) 불린다는 아연실색한 이유로 초기하분포로 불립니다. 분포의 네이밍의 이유는 정말  그럴만한 이유가 있지만 상상 못 할 이유로 가득 차 있습니다-

➌ Gemetric기하분포는 이항분포와 비슷한데, 성공확률이 p인 사건이 첫 번째 발생하기 바로 직전까지의 횟수가 확률변수입니다. 그러니까 마지막이 성공인 확률변수입니다.

➍ Exponential지수분포는 기하분포에서 처음 성공할 때까지의 횟수인 n을 극소하게 시간의 개념으로 나눠서 n→∞를 취함으로써 (여기에서 무한대란 매우 잘게 쪼갠다는 의미입니다.) 다음 성공이 있을 때까지의 시간을 확률변수로 취급하는 분포입니다. Poisson포아송 분포와 마찬가지로 λ를 Parameter로 갖습니다. 참고로 Exponential지수분포는 정해진 발생 확률을 처리합니다만, - 족보에는 나와 있지 않습니다만,- Weibull와이불분포는 시간에 따라 발생 확률이 증가하거나 감소하는 것을 다룸으로써. 더 일반적인 케이스를 다룹니다.

➎ Negative Binomial음이항분포는 r번 성공까지의 "시도 횟수"가 X확률변수입니다. 그러니까, 이항분포는 시행 횟수가 고정되어있고, 성공 횟수가 확률변수인 반면에, 음이항분포는 성공 횟수는 정해져 있고 특정 시도 횟수에 그 성공 횟수가 나올 확률인 셈이죠. 그런데 말이죠, 가끔 엄청 헷갈리게 r번째 성공까지의 실패 횟수를 음이항분포로 설명할 때도 많은데, 이 경우는 Y=X-r 로 변환해서 생각했을 때 Y도 똑같은 분포를 나타내는데 이럴 때 실패 횟수로 표현할 수도 있습니다.

➏ Poisson포아송분포는 이항분포에서 n→∞의 형태로서, 이항분포를 연속형으로 만들었다고 보면 됩니다. 하지만 n과 p를 쓰지 않고, 평균 발생률은 λ = np를 이용해서 계산합니다.

➐ Binomial이항분포가 시행을 많이 하면 Gaussian정규분포가 됨은 이미 살펴보았듯이, 아주 중요한 사실입니다.

➑ t분포는 평균추정에 사용되는데, 일반적인 모분산을 모를 때 표본평균의 분포를 말합니다. 표본이 많아질수록 Gaussian에 근접합니다. 표본이 많아진다는 말은 자유도가 높아질수록이라는 말과 같습니다.

➒ χ²분포는 정규분포들의 제곱합의 분포입니다. 제일 간단한 설명이군요.

➓ F분포는 분자, 분모가 모두 제곱 합으로 표현되는데, 그때의 검정 통계량은 보통 F-분포를 따른다고 보면 되는데, 보통 통계에서 사용되는 제곱의 합은 χ²분포의 비율의 형태로써, 서로 다른 χ²분포의 비율입니다. 보통 통계에서는 분산의 비로 많이 이용됩니다.

⓫ Gamma감마분포는 Exponential지수분포의 일반형인데, n번 사건이 발생할 때까지의 시간이 확률변수입니다. 마치 Negative Binomial음이항 같은 느낌입니다. 대기시간의 모던한 모델로 많이 사용됩니다.

⓬ 마지막으로 Beta베타 분포는 성공과 실패의 비율에 대한 확률 분포인데, 이미 살펴보았듯이, Bayesian 확률분포에서 conjugate prior사전결합분포입니다. 조금 있어 보이는 용어가 하나 출현하는데 conjugate prior. 어 뭔가 어감이 좋습니다. conjugate prior의 뜻은 Bayesian에서 사전확률과 사후확률이 같은 분포를 가질 때 conjuate prior라는 용어를 씁니다.

이제까지 살펴본 관계를 다시 그려보면 다음과 같습니다. 조금 더 자세해졌군요. 그다지 예쁘거나 섹시하지는 않지만, "나쁘지 않아"라는 마음으로 도움이 되었으면 좋겠습니다.