초간단 선형대수. 초간단!이라고 생각해 주세요.
선형대수는 선형 공간에 대한 것들을 문자로 대신해서 표현한 수학의 한 영역입니다. 그렇다면 행렬이 어떤 역할을 하는 것인가?라고 생각하면 행렬이 어떤 입력 벡터에 대한 선형변환이라고 생각하고 그에 대한 체계를 설명한다고 보면 되겠고, 한 가지 더 위대한 사실은 그런 선형 변환의 구현체인 행렬은 주어진 데이터와 곱셈을 함으로써 그 데이터의 차원을 바꾸는 것을 할 수 있다는 점입니다.라는 라고 이야기해 봤자 너무 거창하니까 아주 기초적인 내용을 다루기 위해 다음과 같은 4가지 이야기를 하고 넘어가는 것이 어떨까 합니다.
ⓐ 행렬은 변환임
ⓑ 행렬의 Eigen Value, Eigen Vector는 행렬의 변환에 대한 항등원 비슷한 것임
ⓒ 행렬의 변환에 의한 기존 좌표계의 기저Basis 변환
ⓓ 행렬은 그 자체로 데이터를 설명한다 ★ 매우 중요
이라는 순서로 초간단 선형대수를 살펴볼까 합니다.
ⓐ 행렬은 변환임
일단 정의부터 써 보자면, - '선형대수"라고 하기엔 너무 거창하고 간단한 "행렬곱" 정도의 이해' 편에서 보았던 행렬의 곱은 다른 측면에서 보면 결국에는 벡터(입력)의 선형 변환입니다. 즉, 행렬은 입력 벡터를 변환한다입니다. 어떤 행렬에 (1,1)을 넣으면 (3,7)로 변환되는 예를 보면 이런 식입니다.
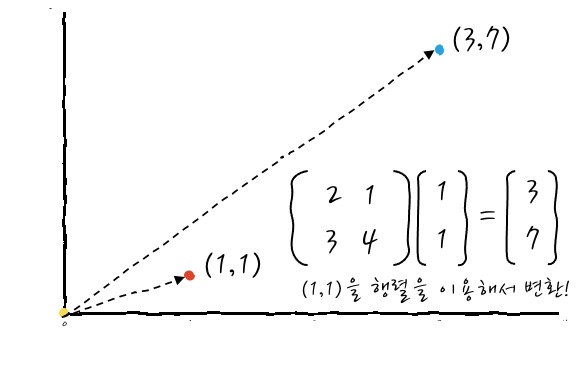
(1, 1) 벡터 1개의 예를 보면 이렇게 보이는데, 아예 가로 0~1 세로 0~1 범위의 사각형에 가득찬 데이터를 이 행렬을 통해서 변환시키면

이런 식으로 변환됩니다(새로운 Vector Space로 변환!). 음 그렇지 그렇고 말고! 하고 무릎을 탁 치고 그냥 넘어갈 수도 있겠지만, 여러 가지 행렬 자체가 가지는 기하학적인 의미를 안다면 머릿속에 행렬을 그리기 편하니까, 여러 가지 의미를 알고 지나가는 것이 여러모로 편리하겠습니다.
ⓑ 행렬의 Eigen Value, Eigen Vector는 행렬의 변환에 대한 항등원 비슷한 것임
제일 먼저 Eigen Vector와 Eigen Value가 무엇인지 조금 살펴볼까 합니다. Eigen Value와 Eigen Vector를 이해하기 위해, 방금 이야기한 행렬이라는 것이 어떤 (입력) 벡터를 선형 변환하는 함수와 비슷하다는 사실을 잘 이해하고 있다면 그닥 다른 이야기가 아니니까 가벼운 마음으로 고고씽.
변환 예에서 보았듯이 입력 벡터(1,1)가 행렬을 통해서 (3,7)로 변환됩니다. - 이제부터 이 선형 변환을 하는 행렬 A는 다음의 행렬을 이용하도록 하겠습니다.
$$
A =
\begin{bmatrix}
2 & 1 \\
3 & 4 \\
\end{bmatrix}
$$ -
자, 그러면 Eigen Vector라는 것을 수식으로 정의할 때 다음과 같이 정의하는데요, 한번 해 봅시다.
$$ Ax = \lambda x \,\,???? $$
이런 관계를 만족하면 x를 Eigen Vector라고 하고요 λ를 Eigen Value라고 한다고 합니다. 이게 수식으로 쓰면 어렵긴 한데, 이 의미를 해석하면, A변환에 대해서 어떤 x vector는 A로 변환했을 때, λ배만큼 크기만 변하고 벡터 자체는 변하지 않는다는 뜻인데, 그걸 만족하는 x를 A행렬에 대한 Eigen Vector, λ를 Eigen Value라고 부릅니다. 이게 처음에 보았을 때는 그게 뭐 별거인가 싶은데, 굉장히 큰 의미를 담고 있더라라는 뭐 그런 반전 아닌 반전이 기다리고 있겠습니다.
자세한 의미는 조금 뒤에 보고, 아주 간단한 Eigen Vector와 Eigen Value를 구하는 것을 쉬어가는 느낌으로 한번 보시죠.
$$ Ax = \lambda x$$ 이니까,
$$ Ax = \lambda I x \\
Ax - \lambda I x = 0 \\
(A-\lambda I)x = 0 $$ 로 식을 정리할 수 있겠습니다.
이때 혹시라도 $(A-\lambda I)$가 역행렬을 가질 수 있다면 $ x = (A-\lambda I)^{-1}0 = 0 $가 되고, x=0 이어야만 하니까, x벡터는 0 벡터가 될 수밖에 없습니다. 그러니까 이때는 우리가 x가 0이 아닌 해를 가져야 하니까 (해가 무수히 많더라도) $ (A-\lambda I) $는 역행렬을 갖지 못해야 합니다. 그래야 $(A-\lambda I)x = 0$를 직접 풀어서 해를 구할 수 밖에 없게 되거든요. 역행렬을 가질 수 없으려면 조건이 $ det |(A-\lambda I)| = 0 $ 이거든요? 이걸 풀면 λ를 구할 수 있고 그 λ에 어울리는 벡터를 구할 수 있겠습니다. (이런 경우 λ는 유일하고, 그것을 만족하는 벡터 x는 무수히 많습니다)
$$
A =
\begin{bmatrix}
2 & 1 \\
3 & 4 \\
\end{bmatrix}
$$ 라고 했으니까, 요걸 실제로 연습문제 풀 듯이 드르르르륵 해보면,
$$
\begin{aligned}
&\begin{bmatrix}
2 & 1 \\
3 & 4 \\
\end{bmatrix}
\begin{bmatrix}
x_1 \\
x_2 \\
\end{bmatrix} =
\lambda
\begin{bmatrix}
x_1 \\
x_2 \\
\end{bmatrix} \\
&\begin{bmatrix}
2 & 1 \\
3 & 4 \\
\end{bmatrix}
\begin{bmatrix}
x_1 \\
x_2 \\
\end{bmatrix} =
\lambda
\begin{bmatrix}
1 & 0 \\
0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
x_1 \\
x_2 \\
\end{bmatrix} \\
&\begin{bmatrix}
2 & 1 \\
3 & 4 \\
\end{bmatrix}
\begin{bmatrix}
x_1 \\
x_2 \\
\end{bmatrix} =
\begin{bmatrix}
\lambda & 0 \\
0 & \lambda \\
\end{bmatrix}
\begin{bmatrix}
x_1 \\
x_2 \\
\end{bmatrix} \\
&\begin{bmatrix}
2 & 1 \\
3 & 4 \\
\end{bmatrix}
\begin{bmatrix}
x_1 \\
x_2 \\
\end{bmatrix} -
\begin{bmatrix}
\lambda & 0 \\
0 & \lambda \\
\end{bmatrix}
\begin{bmatrix}
x_1 \\
x_2 \\
\end{bmatrix}
=0\\
&\begin{bmatrix}
2-\lambda & 1 \\
3 & 4-\lambda \\
\end{bmatrix}
\begin{bmatrix}
x_1 \\
x_2 \\
\end{bmatrix}
=0\\
&\operatorname{det}\left( \begin{bmatrix}
2 & 1 \\
3 & 4 \\
\end{bmatrix}-\lambda\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\right)=0 \\
&\operatorname{det}\left[\begin{array}{cc}
2-\lambda & 1 \\
3 & 4-\lambda
\end{array}\right]=(2-\lambda)(4-\lambda)-1 \cdot 3 = 0 \\
& \lambda ^2 -6 \lambda + 5 = 0\\
&(\lambda-1)(\lambda-5)=0 \\
&\therefore\lambda = 1 \,\, or \,\, 5
\end{aligned} \\
$$
이런 간단한 중학교 수학 소인수 분해 과정을 거쳐서 Eigen Value가 1이거나 5인 것을 찾아냈습니다. 헤헤.
자, 그러면 위 식에 고유값을 넣어서 그 식을 만족하는 (x₁, x₂) 벡터를 구하면, 그 고유값의 짝꿍인 고유 벡터가 됩니다. 자 이제부터 λ=1, λ=5일 때 두 가지를 차례대로 보면,
$$
\left[\begin{array}{cc}
2-\lambda & 1 \\
3 & 4-\lambda
\end{array}\right]\left[\begin{array}{l}
x_1 \\
x_2
\end{array}\right]=\left[\begin{array}{l}
0 \\
0
\end{array}\right]
$$
1) λ = 1 일 때,
$$
\begin{aligned}
&\begin{bmatrix}
2-1 & 1 \\
3 & 4-1 \\
\end{bmatrix}
\begin{bmatrix}
x_1 \\
x_2 \\
\end{bmatrix}
=0\\
& x_1 + x_2 =0 \\
&x_1=-x_2 \\
&\therefore (1, -1)
\end{aligned}
$$
수많은 x₁, x₂중 가장 다루기 편한 크기의 벡터를 임의로 정해 보면 (1, -1)이고요
2) λ = 5 일 때,
$$
\begin{aligned}
&\begin{bmatrix}
2-5 & 1 \\
3 & 4-5 \\
\end{bmatrix}
\begin{bmatrix}
x_1 \\
x_2 \\
\end{bmatrix}
=0\\
&-3 x_1 + x_2 =0 \\
&x_2=3 x_1 \\
&\therefore (1, 3)
\end{aligned}
$$
수많은 x₁, x₂중에 가장 다루기 편한 크기의 벡터를 임의로 정해 보면 (1, 3)입니다.
이렇게, Eigen Value (1, 5) / Eigen Vector ((1, -1), (1, 3))의 pair를 찾아냈습니다. 자, 열심히 찾아내긴 했는데, 이걸 구해서 어디다 쓰냐 그것이 문제로다.라는 질문에 직면하겠습니다. 처음에 언급했던 정의에 의한 접근을 잘 보시면 어떤 변환 행렬 A에 대해서 (1,-1)과 (1,3)는 λ만큼 크기만 바뀌고 방향은 그대로라는 의미니까요. 자, 진짜 그런가 확인해 보죠 머. (1, 3), (1, -1)를 A로 변환해 보면,

어, 뭔가 A행렬에 의해서 (1, 3)는 (5, 15)으로 (1, -1)은 (1, -1)로 - 크기는 다르지만 - 같은 방향을 가진 벡터로 변환됩니다. 참고로 아까 보았던 Eigen Vector가 아닌 (1,1)은 완전히 다른 방향과 크기의 (3,7)로 변환됩니다.
하나씩 자세히 들여다보면,

행렬 A의 Eigen Vector (1,3)은 행렬 A에 의해서 짝꿍 Eigen Value λ=5 만큼 크기만 변합니다. 호.

행렬 A의 Eigen Vector (1,-1)은 행렬 A에 의해서 같은 방향이면서 짝꿍 Eigen Value λ=1 만큼 크기만 변합니다. 호. - 말이 조금 이상하긴 하지만 어쨌든 변환 후의 벡터는 1배 하여 (1,-1)이 되어 원래와 같은 같은 벡터가 되겠습니다 -
그러니까 Eigen Vector는 행렬 A에 의해 방향이 변환이 되지 않는 항등원 같은 Vector인 셈입니다.
조금 더 이해를 돕기 위해서 Gaussian Random Noise Data를 만들어서 이걸 행렬 A를 이용해서 변환해 보겠습니다.

이런 데이터를 변환시키면,
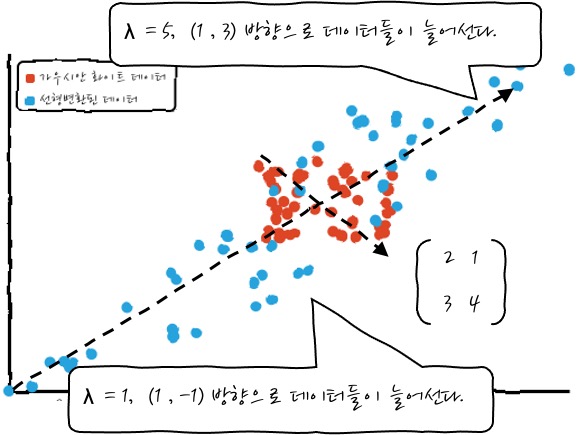
이런 식으로 어떤 방향을 가지고 변환됩니다. 오.
이것이 어떤 의미를 갖는가 하면, A를 통해서 데이터를 변환하게 되면 Eigen Vector들의 방향으로 데이터들이 늘어나서 자리하게 되는데, 이 방향이 Eigen Vector 방향에 Eigen Value 크기 방향입니다. 오. 그렇군요. 이거 신기하군요.
ⓒ 행렬의 변환에 의한 기존 좌표계의 기저 Basis 변환
행렬이 하는 짓을 또 다른 측면에서 바라보면 기저Basis의 변환이라고 할 수 있습니다.
이게 무슨 말이냐면,
어떤 입력 벡터를
$$
\begin{bmatrix}
x_1 \\
x_2 \\
\end{bmatrix}
$$
라고 했을 때 이 입력 벡터는
$$
\begin{bmatrix}
x_1 \\
x_2 \\
\end{bmatrix}
= x_1 \begin{bmatrix}
1 \\
0 \\
\end{bmatrix} + x_2 \begin{bmatrix}
0 \\
1 \\
\end{bmatrix}
$$
으로 다시 쓸 수 있거든요? (1,0), (0,1) 기저의 선형 조합으로 말이죠.
그러면,
$$
\begin{aligned}
A
\begin{bmatrix}
x_1 \\
x_2 \\
\end{bmatrix}
&= A \left(x_1 \begin{bmatrix}
1 \\
0 \\
\end{bmatrix} + x_2 \begin{bmatrix}
0 \\
1 \\
\end{bmatrix}
\right) \\
&= x_1 A \begin{bmatrix}
1 \\
0 \\
\end{bmatrix} +
x_2 A \begin{bmatrix}
0 \\
1 \\
\end{bmatrix}
\end{aligned}
$$
으로 다시 쓸 수 있겠습니다. 이것은??? 수평방향의 기저(1,0)를 A변환한 후에 x₁배, 수직방향의 기저(0,1)를 A 변환한 후에 x₂배 한 것과 같군요?? 그렇다는 이야기는 수평방향의 기저를 변환! 수직방향의 기저를 변환! 하는 이야기인데요. 자 보세요.
$$
\begin{aligned}
&= x_1 \begin{bmatrix}
2 & 1 \\
3 & 4 \\
\end{bmatrix}
\begin{bmatrix}
1 \\
0 \\
\end{bmatrix} +
x_2 \begin{bmatrix}
2 & 1 \\
3 & 4 \\
\end{bmatrix}
\begin{bmatrix}
0 \\
1 \\
\end{bmatrix} \\
&= x_1 \begin{bmatrix}
2 \\
3 \\
\end{bmatrix} +
x_2 \begin{bmatrix}
1 \\
4 \\
\end{bmatrix}
\end{aligned}
$$
어라? (1, 0)이 (2, 3)로, (0, 1)이 (1, 4)으로 변경됩니다. 이 이야기는! (2, 3)와 (1, 4)은 A에 의해 변환되는 벡터의 기저가 된다는 뜻입니다. 호! A에 의해서 변환되는 모든 벡터는 이 새로운 기저 Basis의 선형 합으로 나타낼 수 있다는 뜻입니다.
결국 A를 통해서 Basis 변환이 되는데,
$$
\begin{bmatrix}
x_1 \\
x_2 \\
\end{bmatrix}
= x_1 \begin{bmatrix}
1 \\
0 \\
\end{bmatrix} + x_2 \begin{bmatrix}
0 \\
1 \\
\end{bmatrix} \rightarrow A \rightarrow
x_1 \begin{bmatrix}
2 \\
3 \\
\end{bmatrix} + x_2 \begin{bmatrix}
1 \\
4 \\
\end{bmatrix}
$$
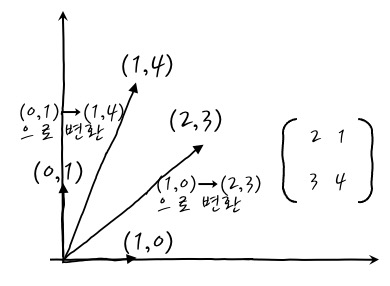
이렇게 다른 변환된 기저의 선형합으로 벡터가 변환된다는 것이죠.
이거 그림으로 보면 조금 느낌이 오는 부분이 있는데! 무엇이냐 하면, 새로운 기저가 행렬의 각 '컬럼'이라는 점입니다. 와 어???

우아앗??? 와 이거 엄청난 정보로군요? 각 basis가 새로운 basis로 변환될 때 행열의 열들과 같군요. 덤덤하게 받아들이는 척하지만, 속으로는 꽤나 놀랍다고 생각합니다. 이렇게 basis가 새로운 basis로 변환되면 새로운 basis의 선형합으로 나타낼 수 있는 공간이 새로 생깁니다.

새로운 Basis로 인하여 공간이 조금은 찌그러져 보입니다만, 어쨌든 이것은 조금은 찌그러진 새로운 공간으로의 변환입니다. 이 새로운 공간에 대한 모든 정보를 행렬 A가 모두 품고 있습니다.
그러니까, A 행렬에 관련한 데이터는

결국 요런 모양새가 되겠습니다. 모두 (1,4) (2,3)의 선형 조합 Linear Combinationdm로 표현이 가능한 데이터들이 되겠습니다. 요.
ⓓ 행렬은 그 자체로 데이터를 설명한다 *매우 중요
이제까지 본 것을 종합해 보면 행렬은 어떤 벡터 데이터를 변환시키는 일을 하게 되는데, 결국에는 행렬과 관계된 벡터의 분포 즉, 모양새를 이미 설명하고 있다고 보면 됩니다.
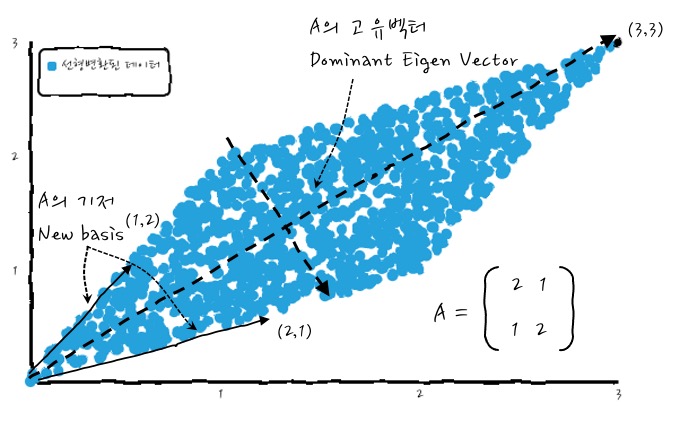
이제까지 살펴본 행렬 A에 대하여 A로 인하여 가질 수 있는 데이터의 모양새는 새로운 기저Basis와 Eigen Vector, Eigen Value를 개념적인 느낌적인 그림으로 설명하기 위해서 합쳐서 보면 대~충 이런 느낌적인 인상을 가질 수 있겠습니다.

이런 모양새가 되겠습니다. 이때 고유값중 가장 큰 값을 갖는 것을 Dominant 하다고 합니다. 이 경우에는 5가 되겠군요. 이런 식으로 새로운 Basis와 Eigen Vector를 합쳐서 보면 뭔가 행렬이 데이터를 설명한다고 볼 수 있겠군요.
더 마음에 와닿도록 종합해서 본다면, - 이것은 가로축이 0~1, 세로축이 0~3으로 uniform distributed 한 데이터를 변환하면 (데이터중에 (1,3) Eigen Vector를 포함하면) 예쁘게 변환되는 것을 볼 수 있습니다.

새로운 기저Basis, Eigen Vector 등을 한눈에 볼 수 있고 이것들이 데이터의 분포를 설명할 수 있겠다고 느꼈다면 그것으로 안심입니다. 많이 왔군요.
자, 그러면 실습을 할 수 있도록 조금은 특별한 경우의 행렬을 가지고 Eigen Value와 Eigen Vector를 구해보도록 하죠.
여기에서, 특별한 경우라는 것은 모든 Element가 양수이고, 대칭 행렬(Symmetry)인 경우의 행렬을 다뤄볼 것인데, 이런 걸 양의 정부호 행렬이라고 합니다. 곧 다룰 PCA를 이해하는데 도움이 되니까 그렇다고 생각해 주세요. 레츠히릿.
$$
\begin{bmatrix}
2 & 1 \\
1 & 2 \\
\end{bmatrix}
$$
요런 행렬인데요. 모두 양의 숫자로 이뤄져 있고, Symmetry 하죠? 자, Eigen Value와 Eigen Vector를 구해야 하겠는데, determinant가 0이어야 하니까 $\lambda_1 + \lambda_2 = 4$이고요, $\lambda_1 \cdot \lambda_2 = 3$ 이니까, Eigen Value는 1, 3이 되겠습니다. 이때의 각각의 Eigen Vector는 (-1, 1), (1, 1)로 구할 수 있겠죠. 아까는 편리한 대로 다루기 편한 크기를 정했었는데, 이 벡터의 크기를 1로 만드는 정규화라는 것을 하게 되면 조금은 표준 느낌으로 Eigen Vector를 정할 수 있겠습니다. 이 정규화를 하게 되면 벡터의 길이가 최대 1이 됩니다. $$ x_1 = \cfrac{1}{\sqrt{2}}
\begin{bmatrix}
-1 \\
1 \\
\end{bmatrix} , \,\,\,\,\
x_2 = \cfrac{1}{\sqrt{2}}
\begin{bmatrix}
1 \\
1 \\
\end{bmatrix}
$$
Eigen Value가 3일 때가 Dominant Eigen Vector이고요. 이걸 파이썬으로 드르르륵해 보면, numpy의 linalg.eig(행렬)를 이용해서 간편하게 구할 수 있습니다.
import numpy as np
m = np.array([[2, 1], [1, 2]])
e, v = np.linalg.eig(m)
이렇게 하면, e(eigen value)와 정규화된 v(eigen vector)를 구할 수 있는데,
e :
array([3., 1.])
v :
array([[ 0.70710678, -0.70710678],
[ 0.70710678, 0.70710678]])
이런 결과를 얻습니다. 이때 주의할 점은 Eigen Vector의 쌍을 읽을 때 행으로 읽으면 안 되고, 열로 읽어야 합니다. 이거 이거 매우 주의해야 하겠군요. 이제까지 손으로 풀어본 정성이 무색할 정도로 간단하군요. 자, 그럼 변환!
u = np.random.uniform(0, 1, (2, 1200))
ret = m @ u # @는 행렬곱임.
이렇게 하면 0~1 사이의 x, y쌍 랜덤 데이터를 만들어 내는데, 요걸 m을 이용해서 변환을 하면 어떻게 되느냐! 하면, 짠!
오, 그렇군요. 그러니까, 데이터와 행렬을 같이 보면 새로운 기저도 보이고, Eigen Value와 Vector가 확실하게 잘 보입니다. 생각보다 긴 이야기가 되어버렸는데, 일단 행렬이 데이터를 이미 설명하고 있다. 그러니까, 행렬을 보고 데이터를 상상할 수 있다는 점만 새겨두어도 큰 수확이라고 생각합니다.

선형대수 상식 1개. 행렬식, Determinant가 0인 경우에 대하여 기하학적인 측면에서 이해. 일단 행렬의 Determinant가 무슨 의미인지부터 보면 좋겠습니다.

일단 어떤 행렬의 Determinant는 행렬의 Basis를 변으로 갖는 평행사변형의 면적입니다. 이 면적으로 행렬의 크기를 정해서 사용하는데요, 행렬의 절대값이라고 보면 좋겠습니다. Determinant의 절대값은 선형 변환의 크기를 나타내고, 부호는 변환되는 데이터의 모양의 보존 여부를 의미합니다.
변환된 면적 = |det(A)| 변환 전 면적
으로 생각하면 좋습니다. 참고로 이게 3차원 이상이 되면 개념상 부피의 개념이 됩니다.
Determinant가 0이라는 의미는 이 면적이 0이라는 뜻이겠습니다. 이것은 행렬을 구성하는 열 벡터가 같은 선상에 있다는 의미입니다. 그렇다고 함은

이렇다는 뜻입니다. 이렇게 되면 이 행렬은 무엇을 변환시키더라도 같은 선상에 있을 수밖에 없습니다. 뭐 그렇다는 이야기입니다. 이건 그냥 determinant가 무엇인지 정도 알고 있으면 좋겠다는 생각에 늘어놓은 이야기입니다.

지금까지 이야기한 모든 행렬에 관한 이야기는 2차원으로 이야기했지만, 3차원, 4차원... 등의 고차원에서도 똑같이 적용되는 이야기입니다. 특히 정방 행렬의 경우에는 - n×n인 경우에는 - Eigen Value와 Vector는 n개가 나온다는 점도 알고 있으면 좋겠습니다.

행렬의 기하학적인 뭐 어쩌구라고 했는데, 기하학이란 도대체 무슨 뜻인가 하면, 幾何의 의미는 중국어로 "얼마?"라는 표현이라는데, "지허"로 발음한다고 합니다. 이것을 우리가 그대로 차용해서 쓰다 보니 우리의 어원과는 거리가 있는 말을 그대로 쓰게 되었다고 하는 것 같습니다. 사실 기하학은 공간에 있는 도형의 성질을 다루니까, 공간도형학 정도로 이름 붙였다면 더 정확하게 의미를 전달할 수 있었을 텐데 말이죠.
 친절한 데이터 사이언스 강좌 글 전체 목차 (정주행 링크) -
친절한 데이터 사이언스 강좌 글 전체 목차 (정주행 링크) - 

댓글