예전엔 식목일이라는 것이 있었는데, 이 날은 공휴일이었습니다. 나무를 심는 일이 얼마나 중요하던지, 모두들 식목일에 나무를 심자.라는 표어를 외치며 나무를 심었었는데요, 가만히 생각해 보면 다른 어떤 휴일날 보다 미래를 위해서 가장 중요한 날임에는 분명한 것 같습니다. 휴일인데 뭔가를 하자는 액션 구호가 있으니 정말 실용적이고 이유 있는 휴일이 아니었나라고도 생각합니다. 식목일이라는 것이 다시 휴일이 된다면 아무런 저항 없이 나무를 심으러 룰루랄라 어딘가로 가지 않을까 생각합니다.
아차, 의사결정나무를 다루려고 보니, 나무 감상에 빠져버렸군요. 어쨌든, 의사결정나무라는 것은 스무고개랑 비슷한 지도학습 방법인데요, 어떤 것을 분류하기 위해서 가장 효율적인 "질문 방법"을 나무 가지가 뻗어 나가듯이 학습을 통해서 찾아내는 것이죠. 이전에 알아보았던 Entropy에 관한 이야기에서 사건들이 모두 같은 확률 일 때는 반씩 나눠서 질문하면 되었었지만, 사건들이 다른 확률을 가졌을 때에는 반씩 나누지 않고, 다르게 나눴었잖아요? 벌써 기억이 나지 않으면 매우 곤란합니다아. 이런 식으로 질문을 통해 효율적인 정보를 알아내는 방법을 자동 구축하는 것이 의사결정나무 모델의 모티브입니다. 그러니까, 이 의사결정나무 모델을 학습시키면 결과물이 if-else 형태의 결정나무 모델이 나오게 되고, 이 모델을 이용해서 분류 예측을 할 수 있습니다. 기계학습 모형 중에 가장 이해하기 쉬운 것이라고 하면 좋겠고, 사실 성능도 꽤 잘 나옵니다.
사실 다음과 같은 그림을 보면, 왜 의사결정나무라고 부르는지도 쉽게 알수 있습니다. 거꾸로 선 나무처럼 생기지 않았나요? 다음의 결정 나무는 여동생이 이제까지 소개팅에 나갔던 데이터를 모아 만든 "여동생은 과연 소개팅에 나갈 것인가?"를 예측하는 결정나무입니다.

어때요, 딱 감이 오죠? 이딴 식의 if-else로 생긴 나무인 것입니다. 일단 이 모형이 어떤 식으로 구성되는지에 대한 구성요소를 이야기해 보면, Node(남자/잘생김/키큼/소개팅/꽝!), Branch(Yes/No), Depth(3깊이)로 이루어져 있습니다. 질문이 node, 답이 branch가 되는 형태입니다.
하하 그렇군요. 그러면 이런 예측 나무를 만들기 위해 어떤 식으로 질문 트리 분할을 할 거냐가 관건이겠군요. 여동생이 이제까지 어떨때 소개팅에 나가더라는 답을 찾기 위해, 기본적으로 각 노드에 순수한 데이터의 비율이 높게 나오도록 질문을 하여 트리를 분할하는 것을 전략으로 합니다. 순수한 데이터 비율이 높다는 것은 무엇인가요?라고 질문한다면,

이런 식으로 순수도를 이용해서 어떤 것이 더 좋은 질문인지 비교를 할 수 있겠군요. 어떤 기준에 대해서 왼쪽 나무는 순수한 데이터끼리 나뉘었고, 오른쪽 나무는 데이터들이 많이 섞였죠? 왼쪽 나무처럼 순수하게 나눌 수록 당연하게도 예측력이 좋습니다.
이런 식으로 잘 분리를 하는 방법에 대해서 그에 맞는 순수도 분리 기준도 당연히 있겠죠.크게 세 가지 방법이 있는데 다음과 같습니다.

이제는 3가지 모두 좀 익숙한 용어들이라고 생각합니다. 이중 하나만 잘 들여다보면 나머지는 똑같은 이야기가 됩니다. 여기에서는 지니 불순도로만 자세히 들여다볼까 합니다.
지니불순도는 지니계수와 같은 맥락인데, 경제학에서 소득 불균형을 지니계수라는 것으로 계산해서 설명하는데, 마찬가지의 의미로 얼마나 불균형한지를 나타내는 것이라고 봐도 어느 정도 의미가 통할 수 있겠습니다.
자, 일단 지니 불순도는 어떤 식으로 계산하는가를 보도록 합시다.
지니 불순도는 1에서 전체데이터중 각각의 레이블이 차지하는 비율을 제곱해서 빼면 됩니다. 예를 들어 5개의 데이터중 레이블 A가 3개 B가 1개 있었다면,
$$ 1- \left( \cfrac{3}{5} \right)^2 - \left( \cfrac{2}{5} \right)^2 = 0.48 $$
입니다. 간단하죠? 일단은 이렇게 걍 계산하고 왜 이렇게 계산하는지는 이야기 마무리를 하면서 다뤄보겠습니다.
여기에서 뜬금없는 정보획득량(Information Gain)이라는 용어가 갑툭튀하게 되는데 이게 뭐냐면 그냥 쉽게 말해서 얼마나 불순도가 차이가 나는가? 에 대한 이야기입니다. 불순도 차이가 나면, 꽤나 큰 정보를 얻었다 정도로 이해하면 되겠습니다. 같은 이야기로, 정보획득량이 크다는 것은 잘 분리했다로 이해하면 되겠죠. 계산은 이전 지니불순도에서 현재 지니불순도의 합을 빼면 됩니다. 결국 이전과 지금의 불순도차이가 얼마나 나는가 하는 이야기 입죠. 그러니까, 정보획득량은 다음과 같이 정의할 수 있겠습니다.
$$IG_{before} - IG_{after}$$
뭐 별건아니고 이런 식으로 그냥 전후의 차이를 계산하는 것뿐입니다. IG는 Information Gain입니다. 전혀 어려운 개념이 아닙니다. 불순도 차이가 많이 나면 이전 단계보다 훨씬 더 잘 분류했다고 보면 되는 그런 겁니다.
자, 어떤 node를 어떤 기준으로 분리했더니 다음과 같았다고 합시다.

일단 루트의 불순도는 0.5이고요, 왼쪽의 node는 순수하게 ★로 이루어져 있으니까 불순도가 0입니다. 그리고 오른쪽은 $1-\left(\cfrac{2}{7}^2 + \cfrac{5}{7}^2\right) = 0.408$ 이 됩니다. 결국, 정보이득은 $0.5-(0+0.408)=0.092$ 가 됩니다. 이런 식으로 불순도 차이가 0.092라고도 할 수 있겠습니다.
그런데, 여기에서 조금 더 고려하면 좋을 것이 있는데, 그것이 무엇이냐면 가중정보이득(Weighted Information Gain)입니다. 이게 머냐면 불순도가 0이어도 다 같은 0이 아니올시다 머 그런건데요.

이걸 보면, 아무래도 불순도가 같은 0이라도 똑같이 취급하기가 좀 그럴수 있겠죠. 그래서 어떤 식으로 하냐면

각각의 node가 가지는 영향력 비율을 곱해서 감안해 줍니다. 그러니까 수정된 가중치 고려 정보획득은
$0.5-(\frac{2}{10}(0.5)^2 + \frac{5}{10}(0.48)^2 + \frac{3}{10}(0.44)^2)$ 으로 계산합니다. 결국 차지하고 있는 데이터의 크기가 작을수록 불순도의 영향력이 작아집니다. 아하.
그러면, 이제는 좀 알 것 같으니까, 실제 예를 가지고 좀 놀아볼까 합니다.

이런 데이터가 있고, 소개팅 성사 결과가 있습니다. 소개팅 성사결과에 대한 불순도는 얼마냐면 0.5겠군요.

두 번째 남자로 해봤더니 남자일 경우에는 소개팅 성사 No가 1개, Yes가 2개가 있고요, 여자일 경우에는 당연하겠지만 No가 1개 있습니다. 그러면 불순도는 남자인가?로 구분하게 되면, 남자일 경우에는 $1-\left(\frac{2}{3}^2+\frac{1}{3}^2\right)=0.444$ 가 되고, 남자가 아닐 경우에는 불순도가 0입니다. 결국 가중치가 적용된 정보이득은 $0.5-(\frac{3}{4}0.444)+\frac{1}{4}0) = 0.1666$ 이 되겠습니다. 자, 그러면 잘생김?으로 한번 구분해 볼까요?
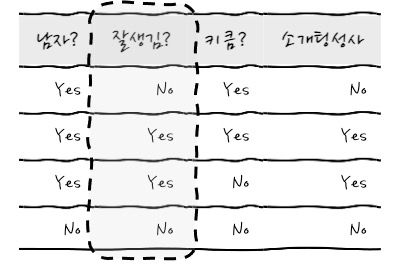
잘생김?으로 구분해 보았더니 잘생긴 그룹에는 소개팅 Yes가 2, 잘생기지 않은 그룹에는 No가 2입니다. 와웃 불순도가 0이군요!
그러면 결국 정보이득은 0.5입니다.
이때, 결과들을 비교해 보면 정보이득이 잘생김?이 훨씬 정보이득이 크기 때문에 가장 최초에 질문해야 하는 질문이 됩니다. 이것이 의사결정나무의 가장 중요한 뽀인트입니다. 가장 큰 노드를 정하고 나면, 그다음부터는 부모 node의 순수도에 비해서 자식 node들의 순수도가 증가하도록 node들을 찾아내는 것입니다.
이런 식으로 구분해 나가다 보면 의사결정나무를 완성할 수 있게 되는데 말이죠, 이런 순서를 찾아내기 위해서 Feature가 A, B, C 세 개를 고려한다면, 다음과 같이 두 개씩 나눠서 지니 불순도의 차이 즉, 정보이득을 계속 구해서 비교하면 의사결정나무를 완성하게 됩니다.
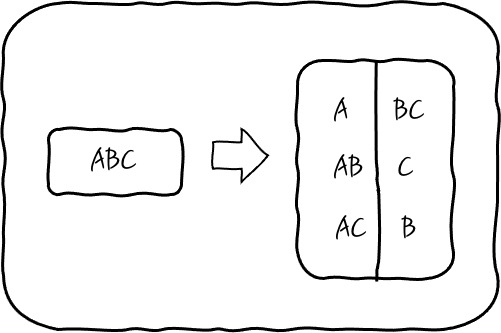
이런 식으로 구한 정보이득에 대해서 정보이득이 가장 큰 순서대로 질문을 배치하면 되는데, 이런 분류 순서를 찾아내기 위해서 모든 경우를 탐색한 후에 더 이상 정보이득이 없을 때까지 찾아낸 후에 중단하는 방식입니다. 여기에서 주의할 것은 무한정 재귀적으로 이런 기준을 찾아내다 보면 당연히 Overfitting이 됩니다. 이런 걸 방지하기 위해 적당한 깊이의 제한을 주거나, 최종 노드의 개수를 제한하는 등의 가지치기(Pruning)를 하기도 하고, 끝까지 트리를 완성한 후에 적당한 수준에서 가지치기를 하거나 합니다. 너무나 당연한 이야기겠죠. 이것이 결정나무의 Hyper Parameter입니다.
이제는 여동생이 소개팅을 할지 안 할지를 미리 예측할 수 있으니 오지랖 부리다가 욕먹는 일은 없을 것입니다.

그래서 이어지는 이야기는 결정 나무를 여러 개 늘어놓아서 숲을 이루게 하는 것이 랜덤 포레스트입니다.

참고로, 지니계수의 산수적 정의는 다음과 같습니다. 지니계수는 숫자가 작을수록 불순도가 없다고 정의합니다. 결국 숫자가 클수록 불순도가 커진다는 점만 알면 되긴 합니다.
$$G = \sum\limits^c_j\sum\limits_{i\neq j} P(i)P(j)$$
어쨌든 수식의 의미는 j Class에 속한 것과 속하지 않은 확률곱이라는 의미인데요, 결국 복원추출로 2개의 표본을 뽑았을 때 i와 j는 같은 Class가 아닐 확률을 의미합니다. i, 와 j 둘 다 확률이 0.5일 때가 가장 가장 불순도가 크고요, 그 이외에는 불순도가 더 작아집니다. 이것을 그래프로 보면 Entropy와 매우 비슷한 특성을 보입니다. 혹시나 파란 구슬과 빨간 구슬을 나누는 행위를 한다고 했을 때, 파란구슬 100%이거나, 빨간구슬 100% 일 때 불순도가 최저입니다. 50%, 50% 일 때 최대값을 갖게 되겠죠.
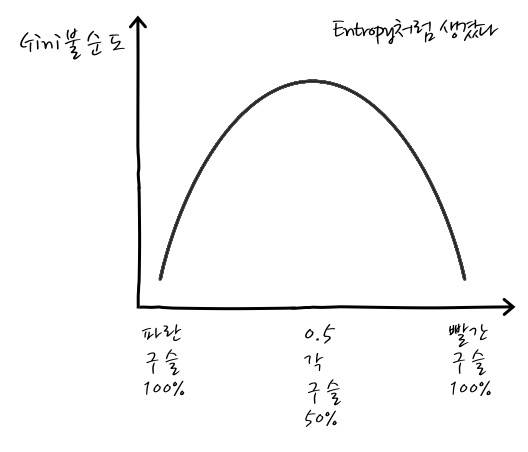
정말 Entropy와 비슷하군요. 최종적으로 지니 불순도의 계산을 어떤 식으로 하냐면, 이중 시그마가 좀 복잡하니까 이중 시그마는 안에서부터 하나씩 고정하고 생각하면 됩니다. 여기에서 안쪽 시그마는 i에 대해서 움직이니까, j는 상수입니다. 그리고, i와 j가 다른 경우라고 했으니
$$ \sum\limits^c_j (1-P(j))P(j)$$ 와 같은 이야기입니다.
이걸 더 정리해 보면
$$ \sum\limits^c_j (P(j)-P(j)^2) = 1-\sum\limits^c_jP(j)^2=1-\sum\limits^c_j \left(\cfrac{n_j}{n}\right)^2 $$
요렇게 되거든요. 이게 Gini Index 수식의 정체입니다요. 아까 계산했던 방식이랑 똑같죠? 제곱의 형태이니까 2차식 형태가 나올 거라는 예상은 쉽게 되겠죠.

엔트로피 지수는 이제는 친근하죠? 무질서 정도에 대한 측정인데, 무질서도가 높을수록 순수도가 낮다고 봐야 하겠습니다.
$$ Entropy = -\sum\limits^k_i p_i log(p_i) $$ 였었는데 리마인드 하면 좋을 것 같고, 이런 Entropy를 순수도로 활용한 학습알고리즘이 C.50라는 것이고,
카이제곱 통계량은 다음과 같았거든요?
$$\chi^2 = \sum\limits_i \cfrac{(O_j-E_j)^2}{E_j} $$ 이 경우에는 카이제곱 통계량이 낮을수록 순수도가 높다고 판단하는데요, 결국 관측도수가 기대도수에 가까워야 분류 예측이 가능하다는 뜻입니다. 조금 어렵게 이야기하면 카이제곱이 예측치에 대한 분산이잖아요? 이 분산이 줄이는 방향으로 자식 node를 찾아내면 예측이 쉽다는 말과 같고, 이 말은 이전에 다룬 것들과 완전히 똑같지는 않지만, 분류에 대한 순수도가 높다고 할 수 있습니다. 결국 관측도수가 기대도수와 많이 다를수록 불순도가 높다고 할 수 있겠습니다. 카이제곱 통계량을 순수도로 활용한 학습알고리즘이 CHAID라는 것입니다. 방금 다룬 지니계수를 순수도로 활용한 학습알고리즘이 CART알고리즘입니다. 덧붙이는 부분이 어째 본문보다 더 길어질 지경이 되겠는데요.

학습 알고리즘에 대한 수식을 보면, 지니불순도는 2지 선다를 할 수 있고, Entropy와 카이제곱은 다지선다를 할 수 있습니다. node에서 branch가 여러 개로 나뉠 수도 있다는 의미입니다.
 친절한 데이터 사이언스 강좌 글 전체 목차 (정주행 링크) -
친절한 데이터 사이언스 강좌 글 전체 목차 (정주행 링크) - 

댓글