드디어 분석이라고 이름이 붙여진 것을 해 볼 차례입니다. 데이터, 통계분석에 관련해서 살펴보았지만, 통계분석은 무엇인가를 알아내기 위해서 데이터를 잘 쪼개서 본 후에 알아낸 것을 주장하게 되는데, 이때 검정을 통해서 분석 결과의 타당성을 뒷받침하는 것이니, ANOVA의 경우에도 그렇겠죠. 표본의 각 집단의 평균의 분산과 각 집단의 표본 분산을 통해서 통계량을 구하는데, 그 통계량만 봐서는 의미를 도출하기 어렵고 그때 구한 통계량을 F검정을 통해 결론까지 도출할 수 있습니다.
ANOVA는 분산분석이라는 이름으로 다짜고짜 소개되는데요. 아니, 잠시만요. 집단간 평균 차이를 결정할 때는 t검정을 이용했는데, 그건 너무 쉽게 알겠습니다만, 3개 이상의 집단 간 평균의 차이를 검정할 때는 분산분석(ANOVA)을 이용한다니 세상에. 아니 갑자기 왠? 분산인 것인가요.
도대체 평균의 차이를 검정하는 데 왠 "분산" 분석인가. 도대체 왜 평균분석을 안하고 분산분석을 하는 것인지 난감하기 짝이 없습니다. 아무리 봐도 분산분석 네이밍 센스 참 어렵네요. 실은 정확하게 말하려면 "분산의 성질과 원리를 이용한 평균 차이 분석"이라고 말하는 것이 정확하다고 생각합니다.만 그래도 좀 어렵긴 합니다. 그러니까, 평균을 직접 비교하지 않고, 집단내의 분산과 각 집단 간의 평균의 분산을 이용해서 평균이 다른지 확인하는 방법이죠. 아하.
결국엔, 집단들의 평균들의 분산이 크면 평균들이 서로 멀리 떨어져 있다고 판단하고, 그러니까 평균이 서로 다르다고 판단하는 방법이고, 거기에 각 집단내의 분산을 같이 고려하는 방법이라고 생각하면 됩니다. 그런 면에서는 ANOVA가 아니라 ANALYSIS OF MEAN DIFFERNECE BY VARIANCE CONCEPT - AMDBV라고 부르는 편이 더 낫겠다는 생각이지만, 입에는 ANOVA가 더 부르기에는 편하군요...
여러 개(3개)의 집단이 있다고 생각해 봅시다.

Intuitively, 집단 평균들 간의 분산이 크고, 집단내의 분산이 작으면 평균이 확실히 다르다는 것을 알아낼 수 있습니다. 그림에서 보면 3개 집단의 분산이 비슷해 보이는데, 그렇게 설명해야 개념적으로 이해하기 쉬워서 그렇게 그린 것뿐입니다.
①②③④케이스에서 ③을 제외한 모든 케이스에서 확실히 평균이 다르다고 단정 지을 수 없습니다. 이것이 ANOVA 분산분석의 아이디어 인데, 그러니까, 집단들의 평균의 분산과 집단내 분산의 비를 가지고 판단해 보자. 그것이 바로 그 정체입니다.
그러면 어떻게 기준을 잡으면 좋을지 생각해 보면, 집단간 평균이 분산이 커지고, 집단내 분산이 작아지는 ③의 경우를 기준으로 찾아낼 수 있다고 생각하면 가장 확실하니까, 더 그 경향이 커질수록 통계량 값이 커지면 좋겠습니다. 그러니까, 평균 제곱 간의 비를 (집단 간 평균의 분산 / 집단 내 분산)으로 정의하면 좋겠습니다. 이때의 검정 통계량 F는 F분포를 따르고, 이 차이가 통계적으로 유의한 지를 분석해서 평균이 모두 같다는 귀무가설을 검증하게 된다는 완전 시시한 얘기입니다.
그러니까, 집단 간 평균의 차이의 제곱 합의 값이 클 수록, 집단 내 평균의 제곱합의 값이 작을수록 평균의 차이가 있다고 판단할 근거가 충분하다고 보는 것입니다.
결국 분산분석(Analysis of Variance)라는 이름만 보고 데이터 분산을 비교하는 방법으로 오해하게 되는 그런 이야기는 이제 그만 잊도록 해요. 분산분석은 표본분산을 이용하여 분석이 수행되므로 지어진 이름이라고. 이에 대해서 헷갈리지 않는 것이 신상에 좋습니다. 에헴.
자, 그러면 이것을 검정하기 위해서 분산의 비는 어떤 분포를 따르는지를 알아야 하는데, 분산 자체는 χ²카이스퀘어 분포를 따른다는 점을 알고 있잖아요? 분자, 분모가 모두 카이스퀘어 분포를 따르는 경우에 이런 비율이 따르는 분포를 찾아낸 것이 Fisher입니다. 이런 공적을 이룬 Fisher의 이름을 따서 F분포라고 이름 지었는데, 이런저런 얘기를 떠나서 이런 이유로 ANOVA 분산분석에서는 F분포를 이용합니다.
자, 여기서 매우 중요한 이야기는 우리가 이용하는 F분포는 Null Hypothesis가 집단간 평균이 같을 경우의 F값(통계량)의 분포입니다. 그러니까, 만일 F분포에서 관측된 F값(통계량)으로 p값을 계산해 보았는데 p값이 너무 작은 경우에는 평균이 서로 같은 환경에서 관측하기 어려운 것이므로 집단 중에 최소한 1개는 평균이 다르다라고 결론을 낼 수 있습니다. 결국에는 모든 분포의 평균은 같다라는 귀무가설을 검정하게 된다고 보면 됩니다.
자, 그럼 조금 더 유식한 말로 풀어보는 과정을 거쳐본다면, F는 분산의 비율을 의미하니까, 아까의 (집단 간 평균의 분산 / 집단 내 분산)으로 정의했는데, 이것을 (Between Mean Variance/ Within Variance)라는 용어로 재정의해 보아요.
이 의미는 Between Mean Variance가 Within Variance에 비해 크면 최소한 1개 그룹은 차이가 난다고 봐야 하겠습니다. Σ (각 그룹의 자신의 분산 즉, Within Variance)으로 정규화 하는 꼴이 되는 것이죠.
그러므로 $F = \cfrac{Mean_{Between}}{Mean_{Within}}$ - 이걸 설명된분산/설명되지않은분산 으로 표기하는데, 도대체 무엇이 설명된 분산이란 말인가, 그리고 무엇이 설명되지 않은 분산이란 말인가. 하면 설명된 분산이란 이미 계산할 값들이 정해지는 경우이고, 설명되지 않은 분산이란 계산 시 이건 케바케로 Random 하게 다르다는 의미로 받아들이면 편합니다.-으로 정의하고, 자유도는 Between의 경우에는 k group-1, Within의 경우에는 n-k (sample-group)이 됩니다. 두 개의 자유도의 합은 n-1 신기하네요. 왜 그런지 한번 살펴보면 k개 그룹으로 mean을 구했으니, k-1 자유도는 잘 알겠고, Within의 경우에는 전체 n개에서 k개 그룹의 mean을 이미 구했으니까, n-k이네요.
그래서 어떤 그룹들의 Between 분산과 Within 분산의 비율인 F_value를 구해보니 10.216이라면 F분포 테이블에서 0.05의 F값은 4.74니까 이 값보다 훨씬 바깥쪽이라서 유의합니다. 그러니까, 유의하다는 것은 Null Hypothesis를 reject한다는 뜻이고, 결국 그룹 간 차이가 있다는 의미입니다. 굳이 p_value를 구해보면 0.008입니다.
그러면 심심하니까, 직접 손으로! ANOVA를 해 볼까요?
예를 들어 다음과 같은 데이터가 있다고 합시다. 이 데이터는 남학생, 여학생, 외계인 학생의 발 길이에 대한 데이터입니다. - 발길이의 모분포는 독립사건의 Count(빈도합)니까 Gaussian이라고 가정할 수 있고 같은 모집단에서 추출한 3집단의 데이터니까 분산의 동질성이 보장된다고 믿고 갑니다. -
boy = [27.3, 28.5, 29.7]
girl = [23.5, 24.2, 22.2, 25.7]
alien = [19.2, 18.6, 17.1]
자, 일단 비교하기 위해서 box plot을 그려보면

뭐 이런 식이군요. 너무 많이 차이가 나다보니까, 이건 뭐. Null Hypothesis 기각이 되어야 정상이겠네요. 하나마나이지만. 한번 해 보겠습니다. 각 집단의 평균에 대한 분산을 구하고 (Between), 각 집단당 평균의 대한 분산을 구해서 (Within)... 룰루 랄라...

$F = \cfrac{⓵/df_{between}}{⓶/df_{within}}= \cfrac{156.66/2}{11.6/7} = 47.268$ 입니다. 뭔지 모르겠지만 꽤 큰 값이네요.
★ 집단별 표본평균의 분산은 중심극한정리에 의해서 $\sigma_x=\cfrac{\sigma}{\sqrt{n}}$이니까, $\sigma^2 = n\sigma_x^2$가 되고, 표본분산을 이용해서 추정한 모분산은 $\sigma^2 = n s_x^2$가 되니까, ①은 각각의 집단의 표본평균의 분산을 각각 구해서 더한 것 즉, 3×(28.5-23.6)² + 4×(23.9-23.6)² + 3×(18.3-23.6)²이고 결국에는 집단 수에 대한 자유도로 평균을 낸 값을 사용할 것이고, ②는 집단내 편차들의 전체 제곱합인데, 결국에는 단순하게 각 집단 내의 모든 편차 제곱을 다 더해서 자유도로 평균을 내서 사용할 것 입니다. ①의 평균/ ②의 평균이 F 통계량입니다. ★
그러면 5% 유의수준으로 검정하면 - 유의 수준 5% 일 때의 F값을 F테이블을 이용해서 구해보면 4.74입니다. -

엇, 엄청나게 p value가 작겠군요.
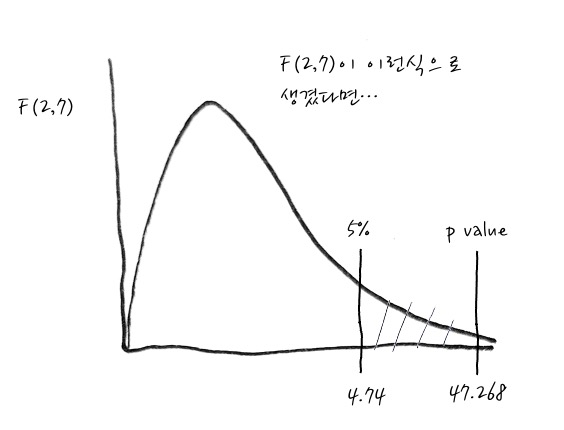
어쨌든, 이렇게 해서 3개의 그룹은 차이가 있다는 결론에 이르릅니다.
이걸 매번 손으로 하기 어려우니까, 소프트웨어의 도움을 받는다면,
from scipy import stats
boy = [27.3, 28.5, 29.7]
girl = [23.5, 24.2, 22.2, 25.7]
alien = [19.2, 18.6, 17.1]
stats.f_oneway(boy, girl, alien)
> 짠! 결과가
> F_onewayResult(statistic=47.26810344827576, pvalue=8.603395069970194e-05)
이렇습니다. p value가 유의 수준보다 엄청나게 작군요. 0.05보다 (엄청나게) 작으니까, 그러면 유의하다고 결론을 이끌어 내고, 3개의 집단은 차이가 있다(모두 같지는 않다)는 결론에 이르면 되겠습니다.
잠깐, 여기에서 one way라는 말이 있는데, 우리말로는 일원분산분석이라고 해서 one way AVONVA라는 것이 있습니다. 이 의미는 우리가 비교하려는 요인의 개수가 1개라는 의미입니다.라는 말이 도대체 무슨 말인가 하는 물음표가 생깁니다. 일(한개)원(원인의)분산(컨셉을이용한)분석이라는 뜻인데, 어떤 것이냐면,
그룹(집단)을 군 또는 수준 이라고도 하고,
요인은 각 그룹(집단)을 구분짓게 하는 것인데, 실험요인/인자/독립변수(Factor) 라고도 합니다.
발길이에 대한 예를 다시 한번 살펴보면 group(boy, girl, alien)이 독립변수, 발길이가 종속변수. 즉, group에 따라 발길이가가 달라지는지 1개의 독립변수와 1개의 종속변수를 검정한 것이라고 할 수 있겠습니다.
조금 억지스러운 예지만 다음과 같이 얘기해 볼 수 있겠습니다.
한 마케팅연구에서 30명의 표본을 선정한 후 이들을 임의로 세 가지 형태의 콜라 광고 중 하나를 시청하게 하였다. 1시간 동안 시청하게 한 후, 광고에 반응하는 것(구매욕구)을 측정하여 세 가지 광고의 차이가 있는지 알고자 한다. 할 때,
측정값 : 구매욕구 (종속변수)
요인 : 광고 (독립변수)
수준 : 3가지 광고
입니다. 광고에 따라 구매욕구가 달라지는가를 연구할 떄, one way ANOVA를 한다고 할 수 있습니다.
게다가, 광고에 따라 그리고, 남/여에 따라 어떻게 되는지 확인하게 되면 two way ANOVA가 됩니다.
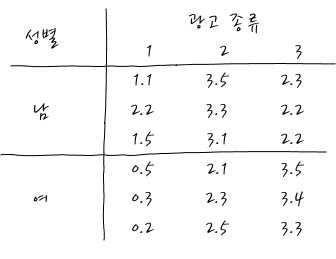
이거 점점 골치아파지네요.

여기에서 의문이 하나 생기는데, 분산이 동질성을 갖게 된다고 해놓고, within variance를 각각 계산하지요? 같을 텐데 뭐하려고 계산했나요? 당연히 하나의 값으로 같아야 하는 것 아닌가?라는 의문이 드는 것이 인지상정이라고 생각합니다. 검정이라는 것을 다시 한번 곱씹어 보면 분산은 한 개의 모집단에서 뽑았다면 동질 하더라도, 어쨌든 표본을 뽑아서 표본분산을 보는 것이니까, 당연히 표본을 뽑을 때마다 그때그때 다른 분산이 될 수밖에 없습니다. 그러니까, 이때의 검정은 Between Variance와 Within Variance 모두 확률변수이고, 그 비가 F분포를 갖게 되는데, 표본을 통해 관측한 경우를 통계량으로 해서 F분포에서 얼마나 어이없는 경우의 관측인지를 확인하는 것입니다. 그러니까 F값이 크면 많이 벌어져 있을 확률이 크기 때문에 집단 중에 최소한 1개는 다르다. 는 결론을 내는 것이죠. 이걸 모르면, 의문투성이의 분석방법이 될 수밖에 없습니다.

많은 집단끼리 차이를 분석할 때 왜 2개 짝지어서 t 검정을 안하는가 하면, 예를 들어 3개 그룹을 비교할 때는 3가지 짝지움을 할 수 있습니다. 이때 1개의 짝지움에 대해 t Test를 하는 경우에는 α=5%로 보았을 때에는 잘못 판단하지 않을 확률이 95%입니다. 이제부터 잘 봐야 하는데, 이걸 Binomial Trial처럼 생각해 보시죠. 3번을 연속해서 검정하게 되는데, 유의하지 않을 확률 95%, 유의할 확률 5%의 동전을 던진다고 할 때, 3번 연속해서 동전을 던진 후에 한 번도 유의하지 않을 확률은 95%×95%×95% 입니다. 그러니까 최소한 한 번이라도 유의할 확률은 1-95%×95%×95%가 되겠습니다. 이렇게 되면 원래 α는 5%로 시작했지만 3번 연속 검정을 하게 되면 1-95%×95%×95% = 0.142625가 되어 약 14.2%정도로 α가 커집니다. 이렇게 되면 원래 5%로 판단하려고 했던 처음 의도와 다르게 14.2%를 기준으로 유의성을 판단하는 것과 같은 효과가 됩니다. 이걸 일반화하면 전체 그룹에서 2개를 뽑는 수만큼 t Test를 하게 되고, 신뢰도는 1-α이므로 $1-(1-\alpha)^{_nC_2} $ 의 형태로 식으로 계산할 수 있겠습니다. 이렇게 되었을 때 유의확률α가 커지니까 False Positive 오류 (Type I Error)를 범할 확률이 커진다고 볼 수 있겠습니다. 이런 오류를 범하지 않을 가능성을 검정력이라고 부릅니다.

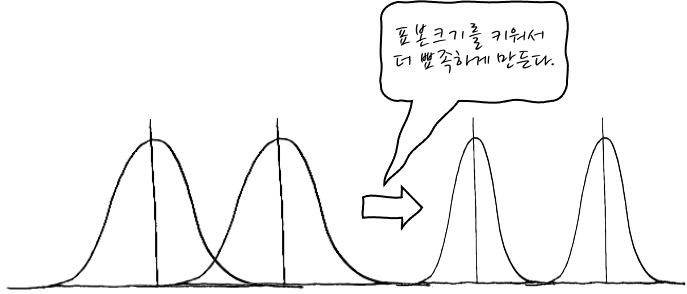
그러면 혹시나 여러번의 t검정을 연속으로 해서 ANOVA를 대신할 수 있는 방법은 무엇이 있는가 하면 표본을 더 많이 뽑아서 표본 평균의 분포를 더 뾰족하게 만들면 검정력이 좋아지겠죠. 그렇지만 현실적인 이야기라고 생각하지 않습니다.

그렇다면 2개 그룹의 평균을 비교할 때는 ANOVA를 쓰면 안되나요? 당연히 가능하며, 등분산의 2개 집단의 검정 결과는 Independent two Samples t-test결과와 ANOVA결과는 p value가 똑같이 나옵니다. 게다가 두 분석의 통계량은 제곱 관계로서, t값을 제곱하면 F값이 나옵니다. 결국 t검정은 ANOVA의 특별한 경우로서, 자유도가 n인 t분포의 제곱은 자유도가 (1,n)인 F분포가 되는 것과 같은 원리입니다.

이렇게 열심히 ANOVA를 해도 결과가 Significant하다면 정확히 어느 그룹의 평균값이 다른지는 알 수 없습니다. 그럼, 이걸 왜 해?라고 묻는 다면, 추가적인 사후분석(Post Hoc Analysis)을 통해서 알아내야 합니다.

마지막으로 ANOVA 내용을 보시다시피 분산의 동질성 가정이 매우 중요합니다. 이 분산의 동질성 가정을 만족하지 못하는 경우에는, Welch 검정을 하게되는데요, 등분산이 아니라면 모집단의 모습은 아마도
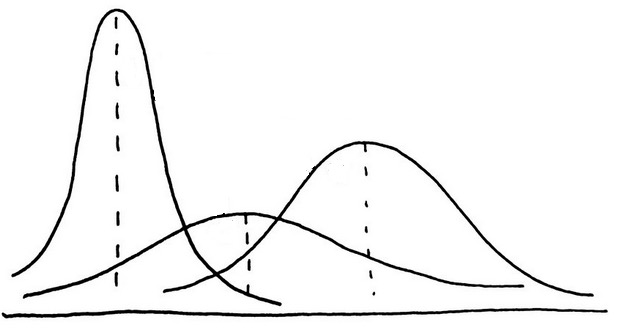
이런 모양새일테니, 조금 곤란하군요. Welch 고마워요. (※ 주의 : 모분포입니다. 표본의 분포가 아닙니다). 미리 살펴보았던 "어디에 어떤 모수 검정과 비모수 검정을 쓸 수 있는지 대탐험 - 그리고 파이썬"편에 Welch 검정하는 법이 있으니까 참고해 주세요.

교차분석과의 차이는 ANOVA는 Categorical - Continuous인데, 교차분석은 Discrete - Discrete라는 차이가 있습니다.
 친절한 데이터 사이언스 강좌 글 전체 목차 (정주행 링크) -
친절한 데이터 사이언스 강좌 글 전체 목차 (정주행 링크) - 

댓글